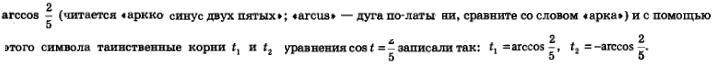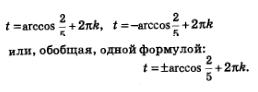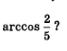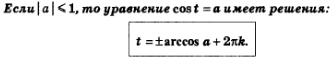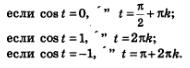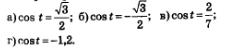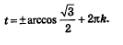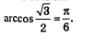|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Арккосинус. Решение уравнения cost = а
§ 17. Арккосинус. Решение уравнения cost = а
В предыдущем параграфе мы отметили, что уравнение вида соs t =а для одних значений а мы решать умеем, а для других — нет. Так, для уравнения
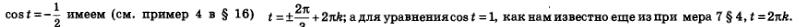
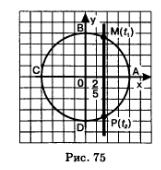
Теперь рассмотрим уравнение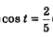 (мы не смогли его решить в примере 2 § 16). С помощью числовой окружности получаем (рис. 75): (мы не смогли его решить в примере 2 § 16). С помощью числовой окружности получаем (рис. 75):
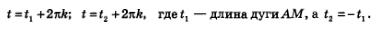
Встретившись впервые с подобной ситуацией, математики поняли, что надо придумать способ ее описания на математическом языке.
Они ввели в рассмотрение новый символ
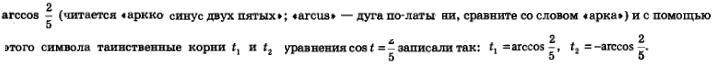
Теперь все корни уравнения 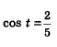 можно описать двумя формулами: можно описать двумя формулами:
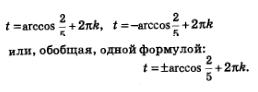
Что же такое 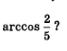 Это — число (длина дуги АМ), косинус которого равен Это — число (длина дуги АМ), косинус которого равен 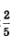 и которое принадлежит первой четверти числовой окружности — отрезку и которое принадлежит первой четверти числовой окружности — отрезку 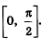
Замечание. Символ агссоs 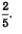 введенный математиками, содержит новый математический знак (агс), напоминание об исходной функции соs t (агссоs) и, наконец, напоминание о правой части уравнения, в приведенном нами случае о числе введенный математиками, содержит новый математический знак (агс), напоминание об исходной функции соs t (агссоs) и, наконец, напоминание о правой части уравнения, в приведенном нами случае о числе 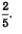 . Вот так в итоге и появился символ агссоs . Вот так в итоге и появился символ агссоs 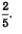 (состоящий как бы из трех частей). (состоящий как бы из трех частей).
Теперь рассмотрим уравнение 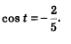 С помощью числовой окружности (рис. 76) получаем: С помощью числовой окружности (рис. 76) получаем:
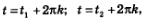

Сформулируем определение арккосинуса в общем виде.
Определение. Если 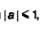 то агссос а (арккосинус а) — это такое число из отрезка [0, п], косинус которого равен а (рис. 77). Итак, то агссос а (арккосинус а) — это такое число из отрезка [0, п], косинус которого равен а (рис. 77). Итак,
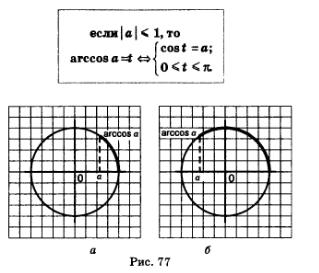
Теперь мы в состоянии сделать общий вывод о решении уравнения соs t =а:
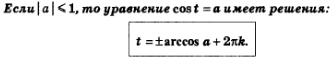
Правда, в трех случаях предпочитают пользоваться не полученной общей формулой, а более простыми соотношениями:
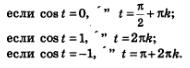
Замечание. Во всех этих формулах, если не оговорено противное, предполагается, что 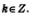 Об этом мы уже договорились выше. Об этом мы уже договорились выше.
Пример 1. Вычислить:
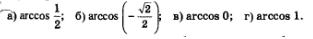
Решение:

Доказательство. Будем считать для определенности, что а > 0. Отметим агссоs а на числовой окружности — это длина дуги АМ и агссоs (-а) — длина дуги АР (рис. 78). Дуги АМ и РС симметричны относительно вертикального диаметра окружности, значит, длины этих дуг равны. Получаем:
агссоs а+агссоs (~а)=АМ+АР=РС+АР=АС = п.
На практике полученное соотношение удобнее использовать в следующем виде:

При этом учитывают, что в случае, когда а> 0, значения агссоs а принадлежат первой четверти числовой окружности.
Например, агссоз 
Такой же результат был получен выше при решении примера 1б.
Пример 2. Решить уравнения:
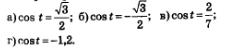
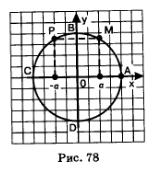
Решение: а) Составим формулу решений:
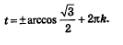
Вычислим значение арккосинуса:
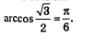
Подставим найденное значение в формулу решений:

Вычислить значение арккосинуса в данном случае мы не можем, поэтому запись решений уравнения оставим в полученном виде.
г) Так как -1,2 <—1, то уравнение соs <=-1,2 не имеет решений (переходить здесь к арккосинусу не имеет смысла).
Пример 3. Решить неравенства: 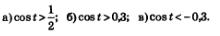
Решение: а) Учтем, что соs t — абсцисса точки М(t) числовой окружности. Значит, нам надо найти такие точки М(t), лежащие на окружности, которые удовлетворяют неравенству 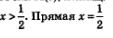 пересекает числовую окружность в двух точках КиР (рис. 79). Неравенству пересекает числовую окружность в двух точках КиР (рис. 79). Неравенству 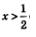 соответствуют точки открытой дуги КР. Дуга КР — это дуга с началом в точке К и концом в точке Р при движении по окружности против часовой стрелки. Главные «имена» точек К и Р в этом случае— соответственно соответствуют точки открытой дуги КР. Дуга КР — это дуга с началом в точке К и концом в точке Р при движении по окружности против часовой стрелки. Главные «имена» точек К и Р в этом случае— соответственно  Значит, ядром аналитической записи дуги КР является неравенство: Значит, ядром аналитической записи дуги КР является неравенство: 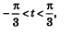 а сама аналитическая запись дуги КР 3 3 а сама аналитическая запись дуги КР 3 3
л „ , л „ , имеет вид: - — + 2пк < X < — + 2пк. 3 3
б) Прямая х = 0,3 пересекает числовую окружность в двух точках КиР (рис. 80). Неравенству х>0,3 соответствуют точки открытой дуги КР. Главные «имена» точек КиР в этом случае — соответственно -агссоз 0,3 и агссоз 0,3. Значит, ядром аналитической записи дуги КР является неравенство:
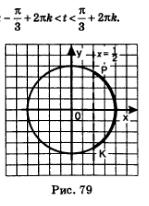
а сама аналитическая запись дуги КР имеет вид
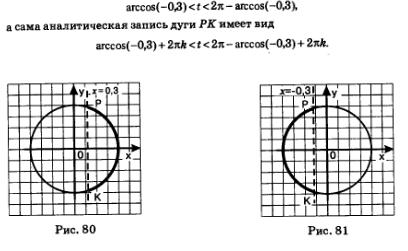
в) Прямая х = - 0,3 пересекает числовую окружность в двух точках К и Р (рис. 81). Неравенству х <- 0,3 соответствуют точки открытой дуги РК. Дуга РК — это дуга с началом в точке Р и концом в точке К при движении по окружности против часовой стрелки. Главные «имена» точек Р и К — соответственно агссоз (-0,3) и 2л- агссоз(-0^). Значит, ядром аналитической записи дуги РК является неравенство:
агссоз(-ОЗ) < < < 2л - агссоз(-0,3), а сама аналитическая запись дуги РК имеет вид
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|