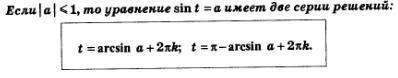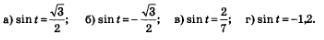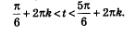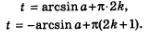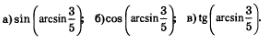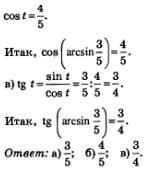|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Арксинус. Решение уравнения sint = a
§ 18. Арксинус. Решение уравнения sint = a
Рассмотрим уравнения 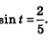 С помощью числовой окружности (рис. 82) получаем: С помощью числовой окружности (рис. 82) получаем:
Что же такое 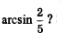 Это — число (длина дуги АМ), синус которого равен Это — число (длина дуги АМ), синус которого равен 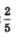 и которое принадлежит первой четверти числовой окружности — отрезку и которое принадлежит первой четверти числовой окружности — отрезку
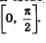
Теперь рассмотрим уравнение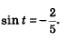
С помощью числовой окружности (рис. 83) получаем:
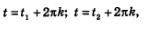
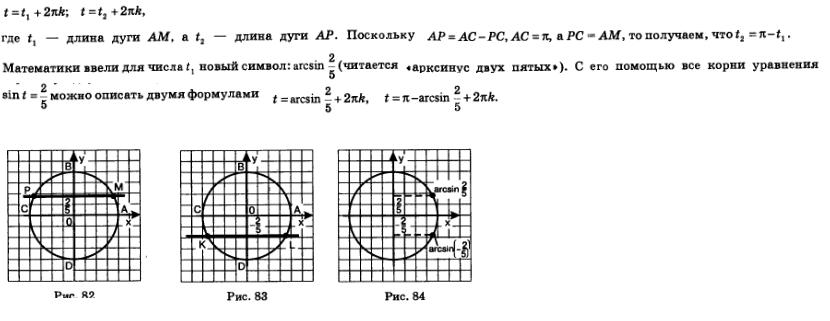
где t1 — длина дуги ВА, взятая со знаком минус, 1г — длина дуги К А, взятая тоже со знаком минус. Математики обозначили число t2 символом 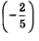 и сразу обратили внимание на два обстоятельства. и сразу обратили внимание на два обстоятельства.
Первое: дуги АМ и АЬ (см. рис. 82 и 83) равны по длине и противоположны по направлению. Значит,
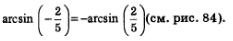
Второе:

Сформулируем определение арксинуса в общем виде.
Определение.
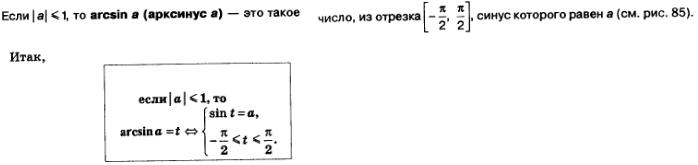
Теперь мы в состоянии сделать общий вывод о решении уравнения t = a:
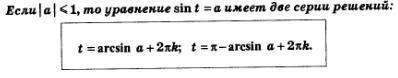
Правда, в трех случаях предпочитают пользоваться не полученной общей формулой, а более простыми соотношениями:
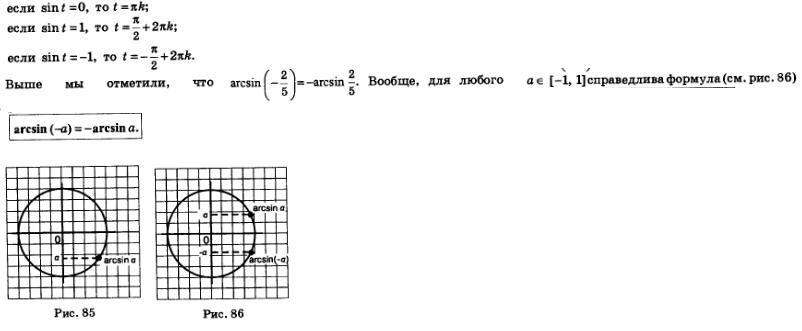
Пример 1. Вычислить:
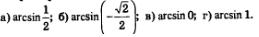
Решение: а) Положим

Пример 2. Решить уравнения:
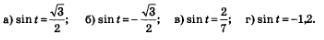
Решение: а)Составим формулы решений:

Вычислить значение арксинуса в данном случае мы не можем, поэтому запись решений уравнения оставим в полученном виде.
г) Так как -1,2 < -1, то уравнение sin t = -1,2 не имеет решений (переходить здесь к арксинусу не имеет смысла).
Пример 3. Решить неравенства:
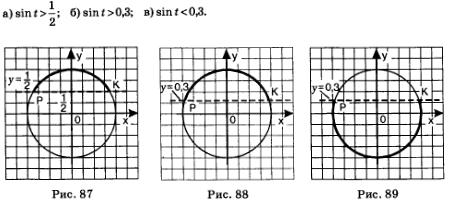
Решение: а) Учтем, что sin t — ордината точки М(t) числовой окружности. Значит, нам надо найти такие точки М(t), лежащие на окружности,
которые удовлетворяют неравенству 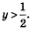 Прямая Прямая 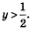 пересекает числовую окружность в двух точках К и Р (рис. 87). Неравенству пересекает числовую окружность в двух точках К и Р (рис. 87). Неравенству 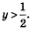 соответствуют точки открытой дуги КР. Главные « имена » точек соответствуют точки открытой дуги КР. Главные « имена » точек
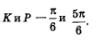 Значит, ядром аналитической записи дуги КР является неравенство Значит, ядром аналитической записи дуги КР является неравенство 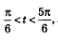 а сама аналитическая запись дуги КР имеет вид: а сама аналитическая запись дуги КР имеет вид:
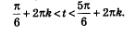
б) Прямая у = 0,3 пересекает числовую окружность в двух точках КиР (рис. 88). Неравенству у > 0,3 соответствуют точки открытой дуги КР. Главные «имена» точек КиР — соответственно агсзт 0,3 и
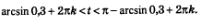
в) Неравенству у <0,3 соответствуют точки открытой дуги РК (рис. 89). Главные «имена» точек Р и К в этом случае . Значит, решение неравенства имеет вид:
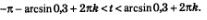
Полученные выше две формулы для решения уравнения sin t =а:
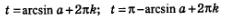
можно объединить одной формулой. Перепишем эти формулы следующим образом:
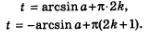
Замечаем, что если перед агсsin а стоит знак «+*, то у числа л множителем является четное число 2к (см. первую строку); если же перед агсsin а стоит знак «—», то у числа л множителем является нечетное число (2й + 1)(см. вторую строку). Это наблюдение позволяет записать общую формулу для решения уравнения sin 1=а:

Почему эта формула общая? Да потому, что при четном n (n- 2к) из нее получается первая из написанных выше формул, а при нечетном n (n = 2к +1) — вторая из написанных выше формул.
С помощью полученной общей формулы можно по-другому записать решения уравнений примера 2. Так, для уравнения

Для рассмотренного в примере 2 в) уравнения 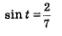 ответ можно записать так: ответ можно записать так: 
Теперь мы можем найти решения уравнения, которое не смогли решить в примере 2 § 16: sin t =-0,3 Имеем
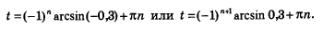
Замечание. Вы, наверное, обратили внимание на то, что мы здесь и в § 17, говоря о решении уравнений и неравенств, все время обозначали переменную буквой 2, а не х, к чему вы, естественно, больше привыкли. Это дало нам возможность более комфортно использовать для решения уравнений и неравенств числовую окружность. Теперь мы имеем готовые формулы для решения уравнений sin t = а, соs t = а. Значит, мы можем обойтись без числовой окружности. А коли так, то в дальнейшем, говоря о тригонометрических уравнениях и неравенствах, вернемся к более традиционному обозначению переменной — обозначению х.
Пример4. Вычислить: 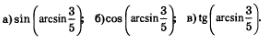
Решение: а) Воспользовавшись определением арксинуса, получим:

Поскольку t принадлежит первой четверти, из двух указанных выше возможностей выбираем первую:
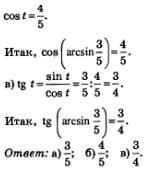
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|