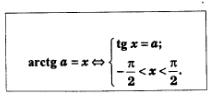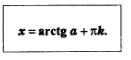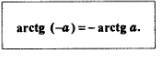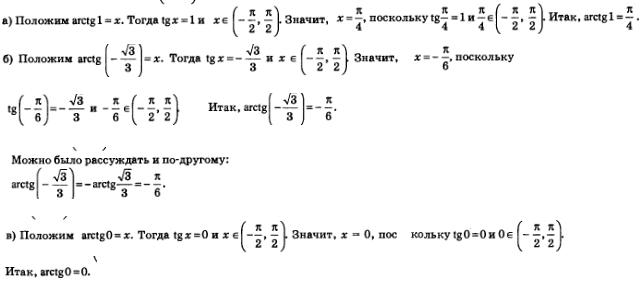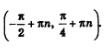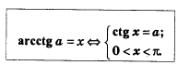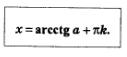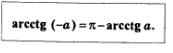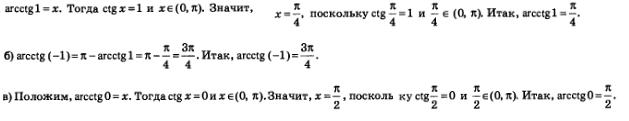|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a
§ 19. Арктангенс и арккотангенс. Решение уравнений tgx = а, ctgx = a
В примере 2 §16 мы не смогли решить три уравнения:
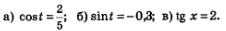
Два из них мы уже решили — первое в § 17 и второе в § 18, для этого нам пришлось ввести понятия арккосинуса и арксинуса. Рассмотрим третье уравнение х = 2.
Графики функций у=tg х и у=2 имеют бесконечно много общих точек, абсциссы всех этих точек имеют вид 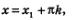 — абсцисса точки пересечения прямой у = 2 с главной ветвью тангенсоиды (рис. 90). Для числа х1 математики придумали обозначение агсtg 2 (читается «арктангенс двух»). Тогда все корни уравнения х=2 можно описать формулой х=агсtg 2 + пк. — абсцисса точки пересечения прямой у = 2 с главной ветвью тангенсоиды (рис. 90). Для числа х1 математики придумали обозначение агсtg 2 (читается «арктангенс двух»). Тогда все корни уравнения х=2 можно описать формулой х=агсtg 2 + пк.
Что же такое агсtg 2? Это — число, тангенс которого равен 2 и которое принадлежит интервалу 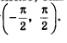
Рассмотрим теперь уравнение tg х = -2.
Графики функций 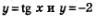 имеют бесконечно много общих точек, абсциссы всех этих точек имеют вид имеют бесконечно много общих точек, абсциссы всех этих точек имеют вид 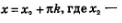 абсцисса точки пересечения прямой у = -2 с главной ветвью тангенсоиды. Для числа х2 математики придумали обозначение агсtg(-2). Тогда все корни уравнения х = -2 можно описать формулой абсцисса точки пересечения прямой у = -2 с главной ветвью тангенсоиды. Для числа х2 математики придумали обозначение агсtg(-2). Тогда все корни уравнения х = -2 можно описать формулой
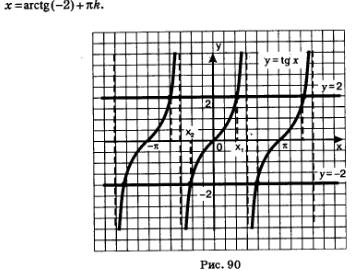
Что же такое агсtg(-2) ? Это—число, тангенс которого равен -2 и которое принадлежит интервалу 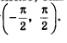 . Обратите внимание (см. рис. 90): х2 = -х2. Это значит, что агсtg(-2) = - агсtg 2. . Обратите внимание (см. рис. 90): х2 = -х2. Это значит, что агсtg(-2) = - агсtg 2.
Сформулируем определение арктангенса в общем виде.
Определение 1. агсtg а (арктангенс а) — это такое число из интервала 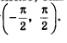 , тангенс которого равен а. Итак, , тангенс которого равен а. Итак,
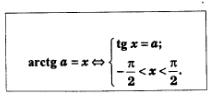
Теперь мы в состоянии сделать общий вывод о решении уравнения х=а: уравнение х = а имеет решения
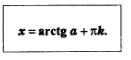
Выше мы отметили, что агсtg(-2) = -агсtg 2. Вообще, для любого значения а справедлива формула
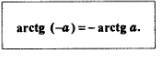
Пример 1. Вычислить: 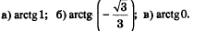
Решение:
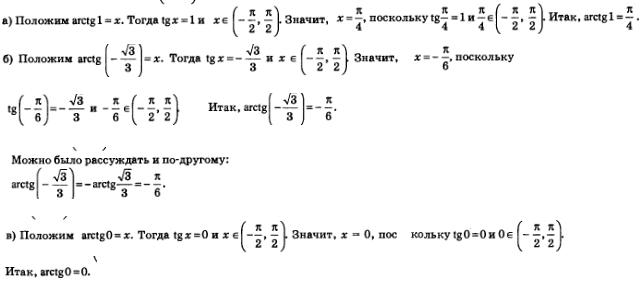
Пример 2. Решить уравнения: 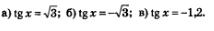
Решение: а) Составим формулу решений:

Вычислить значение арктангенса в данном случае мы не можем, поэтому запись решений уравнения оставим в полученном виде.
Ответ: 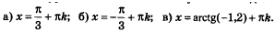
Пример 3. Решить неравенства: 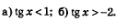
Неравенство вида 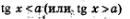 можно решать графически, придерживаясь следующего планам можно решать графически, придерживаясь следующего планам
1) построить тангенсоиду у = tg х и прямую у = а;
2) выделить для главной ветви тангейсоиды промежуток оси х, на котором выполняется заданное неравенство;
3) учитывая периодичность функции у = tg х, записать ответ в общем виде.
Применим этот план к решению заданных неравенств.
Решение: а) Построим графики функций у = tgх и у = 1. На главной ветви тангенсоиды они пересекаются в точке
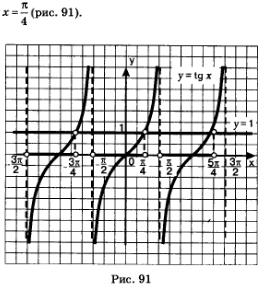
Выделим промежуток оси х, на котором главная ветвь тангенсоиды расположена ниже прямой у = 1, — это интервал 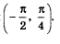
Учитывая периодичность функции у = tgх, делаем вывод, что заданное неравенство выполняется на любом интервале вида:
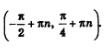
Объединение всех таких интервалов и представляет собой общее решение заданного неравенства.
Ответ можно записать и по-другому:
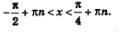
б) Построим графики функций у = tg х и у = -2. На главной ветви тангенсоиды (рис. 92) они пересекаются в точке х = агсtg(-2).
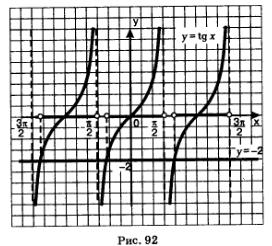
Выделим промежуток оси х, на котором главная ветвь тангенсоиды

Рассмотрим уравнение с tg х=а, где а>0. Графики функций у=сtg х и у =а имеют бесконечно много общих точек, абсциссы всех этих точек имеют вид: х = х1 + пк, где х1 =агссtg а — абсцисса точки пересечения прямой у=а с главной ветвью тангенсоиды (рис. 93). Значит, агссtg a — это число, котангенс которого равен а и которое принадлежит интервалу (0, п); на этом интервале строится главная ветвь графика функции у =сtg х.
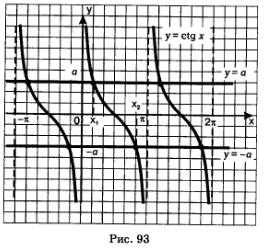
На рис. 93 представлена и графическая иллюстрация решения уравнения с1tg = -а. Графики функций у =сtg х и у = -а имеют бесконечно много общих точек, абсциссы всех этих точек имеют вид х = х2 + пк, где х2 = агссtg (- а) — абсцисса точки пересечения прямой у = —а с главной ветвью тангенсоиды. Значит, агссtg(-а) — это число, котангенс которого равен -а и которое принадлежит интервалу (О, п); на этом интервале строится главная ветвь графика функции У =сtg х.
Определение 2. агссtg а (арккотангенс а) — это такое число из интервала (0, п), котангенс которого равен а.
Итак,
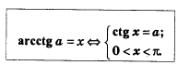
Теперь мы в состоянии сделать общий вывод о решении уравнения сtg х=а: уравнение ctg х = а имеет решения:
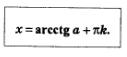
Обратите внимание (см. рис. 93): х2 =п-х1. Это значит, что
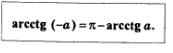
Пример 4. Вычислить:
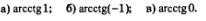
Решение: а) Положим,
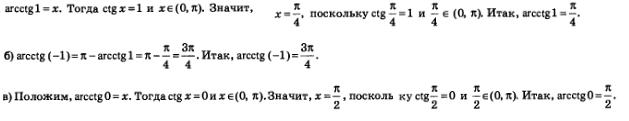
Уравнение сtg х=а практически всегда можно преобразовать к виду 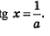 Исключение составляет уравнение сtg х =0. Но в этом случае, воспользовавшись тем, что можно перейти к Исключение составляет уравнение сtg х =0. Но в этом случае, воспользовавшись тем, что можно перейти к
уравнению соs x=0. Таким образом, уравнение вида х=а самостоятельного интереса не представляет.
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|