|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Геометрические фигуры. Полные уроки ТЕМА УРОКА: Высота, биссектриса и медиана треугольника Цели урока:
План урока:
Обозначения:
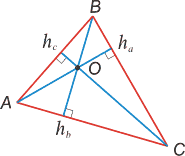
Высота, биссектриса и медиана треугольника Файл:O.gif Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные сторонам треугольника: Файл:13112010 12.gif Файл:13112010 1.gif
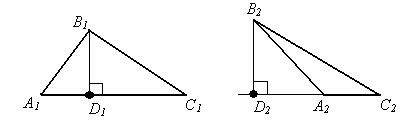
Файл:O.gif Высотой треугольника называется перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на ее продолжение.
B1D1 – высота треугольника A1B1C1, опущенная из вершины B1. B2D2 – высота треугольника A2B2C2, опущенная из вершины B2. Соотношение высот и сторон треугольника. Файл:13112010 13.gif Файл:13112010 14.gif Высота в равностороннем треугольнике. Файл:13112010 15.gif Файл:13112010 16.gif
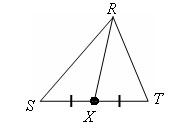
Файл:O.gif Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны.
Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противоположной стороны треугольника.
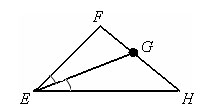
Файл:O.gif Биссектрисой треугольника называется отрезок биссектрисы любого угла от вершины до пересечения с противоположной стороной. Файл:O.gif Биссектрисой угла называется луч, делящий угол пополам. Файл:O.gif Биссектрисы треугольника пересекаются в одной точке, являющейся центром впмсанной окружности.
Биссектрисой треугольника, проведенной из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой противолежащей стороны.
Медиана, биссектриса, высота Высоты и стороны треугольника
Пошаговое построение Медиана треугольника - это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны. Поэтому, для построения медианы необходимо выполнить следующие действия: Биссектриса треугольника - это отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противоположной стороне. Поэтому, для построения биссектрисы необходимо выполнить следующие действия: Высота треугольника - это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противоположную сторону. Поэтому, для построения высоты необходимо выполнить следующие действия: Задание для самостоятельной проверки. 1 вариант: Построить медиану остроугольного треугольника. как построить медиану с помощью циркуля.
Интересный факт: В конце I в. н. э. надо отметить появление трудов неопифагорейца Никомаха. Его работа «Введение в арифметику» является первым трудом по арифметике, изложенным независимо от геометрии, и потому она оказывала свое влияние на изучение арифметики не менее тысячи лет. Между тем эта работа не содержит в себе ничего особенно оригинального. Основной ее идеей является классификация чисел, причем она проводится на основах, всецело опирающихся на числовую мистику. В числовую классификацию Никомаха входят также и многоугольные числа по образцу пифагорейских. Наиболее интересным в «Арифметике» Никомаха является раздел суммирования числовых рядов. Здесь мы встречаем, например, указание на то, что кубические числа представляют собой суммы последовательных нечетных чисел. Так, 13 = 1; 23 = 3 + 5; 33 = 7 + 9 + 11; 43 = 13 + 15 + 17 + 19 и т. д. Вопросы:
Список использованных источников:
Отредактировано и выслано Потурнаком С. А. Над уроком работали Потунак С. А.
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: