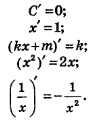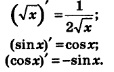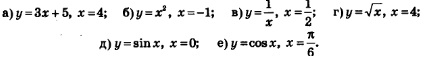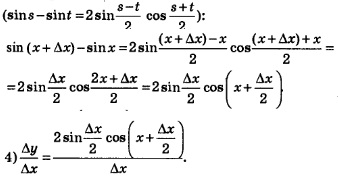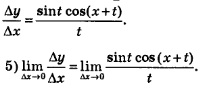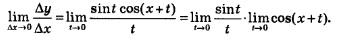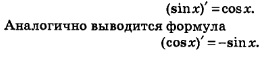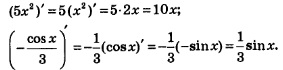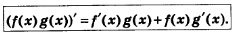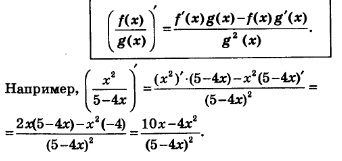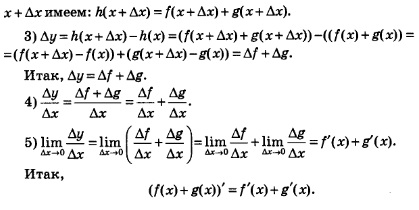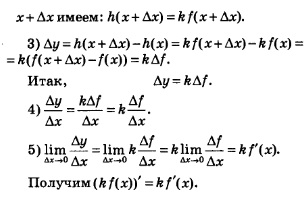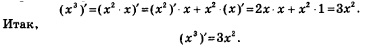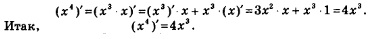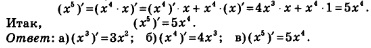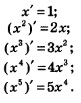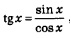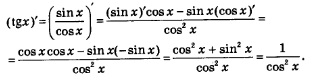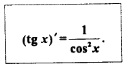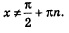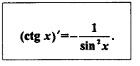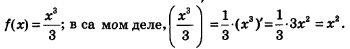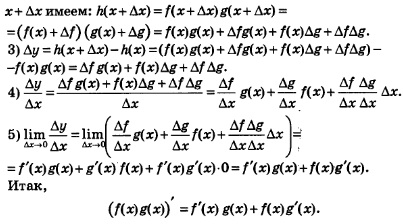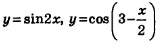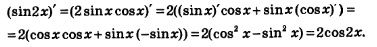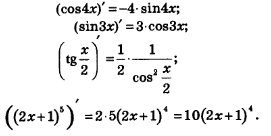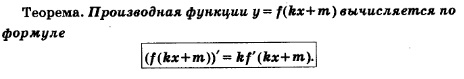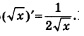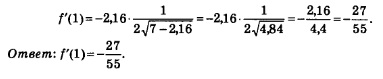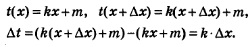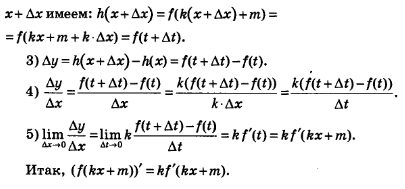|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Вычисление производных
§ 33. Вычисление производных
1. Формулы дифференцирования
Формулами дифференцирования обычно называют формулы для отыскания производных конкретных функций, например:
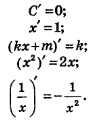
Вы, конечно, узнали эти формулы — они были получены нами в §32.
Список формул дифференцирования будет постепенно пополняться. Здесь мы добавим три формулы, которые выводятся по алгоритму, приведенному в § 32. Определенные технические трудности при этом, естественно, возникают. Поступим так: сначала укажем новые формулы дифференцирования, потом разберем несколько примеров, а в конце покажем новые формулы. Итак, сообщаем три формулы дифференцирования:
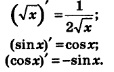
Пример 1. Найти значение производной данной функции в данной точке: 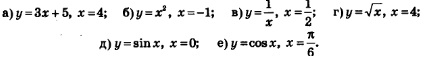
Решение. а) Имеем: (Зх + 5)'= 3, значит, производная равна 3 в любой точке х, в частности, в заданной точке х =4.
Итак, производная функции у = 3х + 5 в точке х =4 равна 3; на математическом языке это удобнее записывать так:
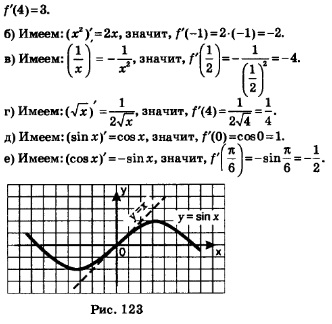
Важное замечание. Когда в главе 1 мы строили график функции у = sin х, то обратили ваше внимание наследующее обстоятельство: из начала координат синусоида выходит как бы под углом 45° (рис. 123). И там же сознались: почему это так, мы пока объяснить вам не можем, соответствующий разговор будет позднее. «Момент истины» наступил.
Мы только что видели, что для функции y = sin х выполняется равенство: 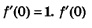 в данном случае — это угловой коэффициент касательной к графику функции у = sin х в точке х=0. Если угловой коэффициент прямой равен 1, то прямая образует с положительным направлением оси х угол 45°. Это обстоятельство и учитывается при построении графика функции у= sin х. в данном случае — это угловой коэффициент касательной к графику функции у = sin х в точке х=0. Если угловой коэффициент прямой равен 1, то прямая образует с положительным направлением оси х угол 45°. Это обстоятельство и учитывается при построении графика функции у= sin х.
Пример 2. Составить уравнение касательной к графику функции у = х2 в точке х = 1.
Решение. Уравнение касательной, как уравнение всякой прямой, имеет вид у=кх + m. Найдем сначала к — это угловой коэффициент касательной, который, как мы знаем, равен f'(1).
Имеем: (х2)'= 2х, значит, f'(1)=2 1=2.
Итак,к = 2, т.е. уравнение касательной надо искать в виде у=2х +m.
Осталось найти значение коэффициента m. Для этого воспользуемся тем, что касательная проходит через точку на параболе у = х2 с абсциссой х = 1, т.е. через точку (1; 1).
Имеем:
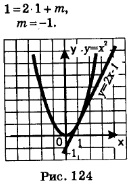
Итак, уравнение касательной имеет вид у = 2х -1. На рис. 124 изображена парабола у = х2 и построена прямая у = 2х-1; чертеж наглядно демонстрирует, что эта прямая касается параболы в точке (1; 1).
Ответ: у = 2х-1.
A теперь выполним данное выше обещание: выведем новые формулы дифференцирования.
Найдем производную функции 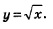 . Воспользуемся алгоритмом отыскания производной. . Воспользуемся алгоритмом отыскания производной.
1) Для фиксированного значения х (разумеется, мы полагаем, что х > 0) имеем:

Найдем производную функции у = sin х. Воспользуемся алгоритмом отыскания производной.
1) Для фиксированного значения х имеем: f(х) = sin х.
2) В точке 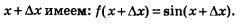
3) 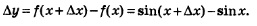 Преобразуем полученное выражение, воспользовавшись формулой «разность синусов» Преобразуем полученное выражение, воспользовавшись формулой «разность синусов»
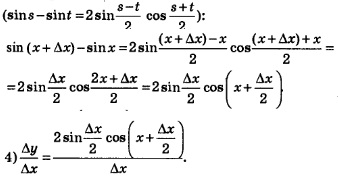
В правой части полученного равенства — обратите внимание — три раза содержится выражение 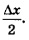 . .
Есть смысл обозначить его буквой t. Получим:
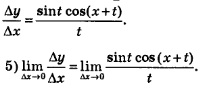
А далее рассуждаем так: 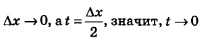 и под знаком предела вместо условия и под знаком предела вместо условия 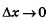 можно записать условие можно записать условие 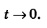 Таким образом, Таким образом,
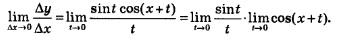
Получили произведение пределов. Первый предел равен 1 (см. п. 2 § 31). А второй предел равен соs х. В итоге получаем соs х.
Итак,
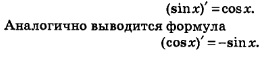
2. Правила дифференцирования.
Здесь речь пойдет о правилах нахождения производных суммы, произведения, частного функций. Приведем эти правила.
Правило 1. Если функции у = f(х) и у = g(х) имеют, производную в точке х, то и их сумма имеет производную в точке х, причем производная суммы равна сумме производных:
(f(х) + 8(х))' =f (х)+ (х).
На практике это правило формулируют короче: производная суммы равна сумме производных. При этом речь может идти о дифференцировании суммы любого числа функций.
Например, 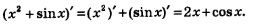
Правило 2. Если функция у = f(х) имеет, производную в точке х, то и функция у = кf(х) имеет производную в точке х, причем:
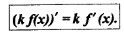
На практике это правило формулируют короче: постоянный множитель можно вынести за знак производной. Например,
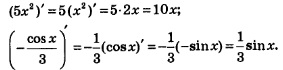
Правило 3. Если функции у=f(х) и у =g(х) имеют производную в точке х, то и их произведение имеет производную в точке х, причем:
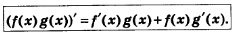
На практике это правило формулируют так: производная произведения двух функций равна сумме двух слагаемых. Первое слагаемое есть произведение производной первой функции на вторую функцию, а второе слагаемое есть произведение первой функции на производную второй функции.
Например: 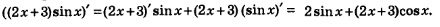
Правило 4. Если функции у = f(x) и у=g(х) имеют производную в  то и частное то и частное  имеет производную в точке х, причем: имеет производную в точке х, причем:
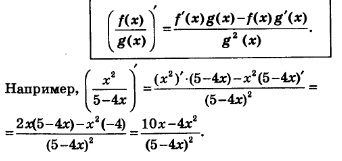
Дальнейший план изложения материала в этом пункте будет таким. Сначала мы выведем первые два правила дифференцирования — это сравнительно нетрудно. Затем рассмотрим ряд примеров на использование правил и формул дифференцирования, чтобы вы к ним привыкли. В самом конце пункта мы приведем доказательство третьего правила дифференцирования — для тех, кому это интересно.
Выведем правило дифференцирования функции у = f(х) + g(х).
Воспользуемся алгоритмом отыскания производной.
1) Положим, ради удобства, f(х) + g(х) = h(х). Для фиксированного значения х имеем: h(х) = f(х) + g(х).
2) В точке
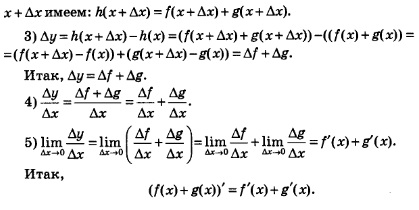
Выведем правило дифференцирования функции у = к f(х). Воспользуемся алгоритмом отыскания производной.
1) Положим, ради удобства, kf(х) = h(х). Для фиксированного значения х имеем: h(х) = кf(х).
2) В точке
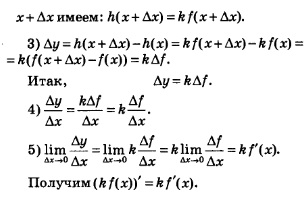
Пример 3. Найти производную функции у=Зх2 -4х + 2.
Решение. Имеем:
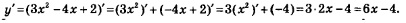
Мы воспользовались первым и вторым правилами, а также формулами дифференцирования линейной функции у = -4х + 2 и функции у = х2.
Ответ: у'=6х-4.
Пример 4. Найти производные функций: а) у = х3; б )у = х4; в )у = х5.
Решение. а) Представим х3 в виде х2 ■ х и применим правило дифференцирования произведения. Получим:
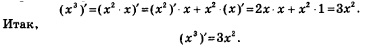
б) Представим х2 в виде х3 ■ х и применим правило дифференцирования произведения. Получим:
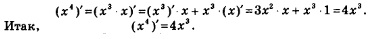
в) Представим х5 в виде х4 ■ х и применим правило дифференцирования произведения. Получим:
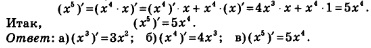
А теперь сравним пять формул: две формулы, которые мы знали раньше, и те три формулы, которые мы вывели в примере 4. Смотрите:
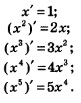
Возникает естественная гипотеза: для любого натурального показателя п справедлива формула дифференцирования:

Важное замечание. «Естественная гипотеза» —это стилистический оборот из области интуиции. Интуиция хороша для открытия новых фактов, но не для их обоснования. Формулу (1) мы «прочувствовали», но строго не обосновали. Приведем (для интересующихся) строгое доказательство.
Мы знаем, что х'= 1. Эту формулу можно переписать в виде (х1)' = f-х°. Значит, формула (1) верна для п =1.
Предположим, что формула (1) верна для натурального числа п=к, т.е. предположим, что верно равенство: (х2)' = кх2~1. Докажем, что тогда формула (1) верна и для следующего натурального числа п = к + 1, т.е. докажем, что 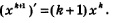
В самом деле имеем:
Итак, для п = 1 формула (1) верна — это мы проверили. Далее, мы доказали, что если формула (1) верна для п = к, то она верна и для п = к +1 Воспользуемся этим: формула (1) верна для п = 1, значит, она верна и для следующего числа п = 2; так как она верна для п =2, то она верна и для следующего числа п =3и т.д. Значит, формула (1) верна для любого натурального числа п.
Использованный здесь метод рассуждения носит в математике название метод математической индукции.
Пользуясь формулой (1) и соответствующими правилами дифференцирования, можно найти производную любого многочлена.
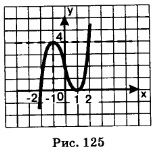
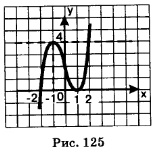
Пример 5. Найти точки, в которых касательная к графику функции у = х3 - Зх + 2 параллельна оси х.
Решение. Имеем: у'=(х3 -3х + 2)'=3х2 -3. Если касательная параллельна оси х, то ее угловой коэффициент равен нулю. Но, с другой стороны, угловой коэффициент касательной равен значению производной в абсциссе точки касания. Значит, нам нужно найти точки, в которых производная обращается в нуль. Имеем: Зх2 -3=0; находим: х1 =1,х2 =-1. Далее,f(1)=13 -3 1+2 = 0; f(-1)=(-1)3-3 (-1)+2=4. Итак, касательная, проведенная к графику функции у = х3 -Зх + 2в точке (1; 0) или в точке (-1; 4), будет параллельна оси х. На рис. 125 дана геометрическая иллюстрация полученного результата — построен график функции у=х3-Зх+2. При этом мы учли, что f(-2)=0, т.е. график пересекает ось абсцисс в точке х = -2.
Пример 6. Найти производные функций: а) у = tg х; б) у = сtg х.
Решение, а) Воспользуемся тем, что 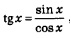 и правилом дифференцирования частного. Получим: и правилом дифференцирования частного. Получим:
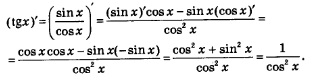
Таким образом, мы вывели еще одну формулу дифференцирования:
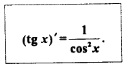
Понятно, что эта формула справедлива лишь при допустимых значениях х, т.е. при 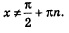
б) Рассуждая аналогично (советуем вам выполнить соответствующие рассуждения), получим:
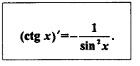
В математике наряду с прямой задачей часто решают обратную. До сих пор мы говорили о том, как по функции найти ее производную. Но часто бывает так, что известна производная, а найти нужно саму функцию. Если, например, известно, что f'(x) =соs х, то f(х) = sin х; в самом деле, производная от sin х равна соs х. Если известно, что f'(х) = х2, то нетрудно догадаться, что
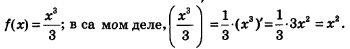
Далее в § 37 мы подробнее поговорим о решении обратных задач, т.е. о том, как, зная производную функции, найти саму функцию.
Завершая этот пункт, выполним данное выше обещание, выведем правило дифференцирования произведения, т.е. функции y = f(х)g(х).
Воспользуемся алгоритмом отыскания производной.
1) Положим, ради удобства, f(х)g(х) = h(х). Для фиксированного значения х имеем: f(х) = h{х)g(х).
2) В точке
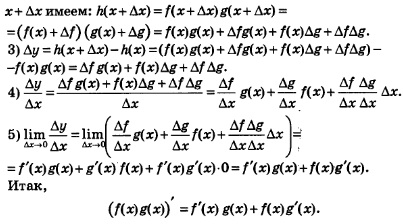
3. Дифференцирование функции у = f(кх+m)
Мы знаем, чему равны производные функций: 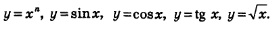 . Нередко на практике приходится находить производные функций . Нередко на практике приходится находить производные функций 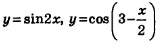 и т.д. Возникает вопрос: если мы знаем, чему равна производная функции у = f(х), то как вычислить производную функции у = f(кх+m)? и т.д. Возникает вопрос: если мы знаем, чему равна производная функции у = f(х), то как вычислить производную функции у = f(кх+m)?
С функцией у = sin2х можно поступить так. Известно, что sin2х = 28 созх. Тогда:
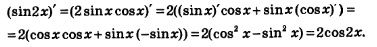
Воспользовавшись правилом дифференцирования произведения и правилом вынесения постоянного множителя за знак производной, а также формулами синуса и косинуса двойного аргумента, мы доказали, что 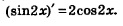
Хорошо, скажете вы, а как быть с производной функций у = sinЗx, у= соs4x? Неужели каждый раз придется применять соответствующие формулы тригонометрии? Отвечаем: не придется. Обратите внимание на выведенную формулу. Чем она отличается от формулы дифференцирования функции у = sin х? Только тем, что появился дополнительный множитель 2, да в роли аргумента выступает не х, а 2х. Точно так же будет обстоять дело и в других аналогичных случаях: используется известная формула дифференцирования и появляется дополнительный множитель, равный коэффициенту при х. Например, справедливы следующие формулы:
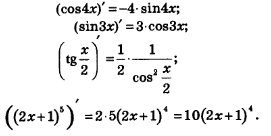
Вообще, справедливо следующее утверждение.
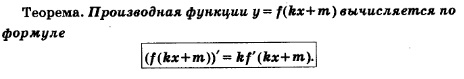
Доказательство теоремы приведем после решения примера.
Пример 7. Найти значение производной функции у = f(х), где 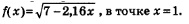
Решение. Сначала найдем производную в произвольной точке х. Известно, что 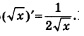 По этой формуле найдем интересующую нас производную, но при этом учтем два обстоятельства: По этой формуле найдем интересующую нас производную, но при этом учтем два обстоятельства:
1) под знаком корня напишем не х, а 7- 2,16х; 2) укажем дополнительный множитель, равный -2,16, — это коэффициент при х. Таким образом,
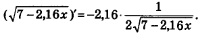
Чтобы вычислить f'(1), в полученное выражение подставим х = 1:
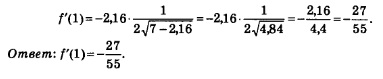
Завершая этот параграф, докажем сформулированную выше теорему.
Введем обозначение 1 = кх+m и заметим,,что если аргументу х придать приращение 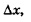 то переменная t получит приращение к • то переменная t получит приращение к • 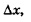 . В самом деле, . В самом деле,
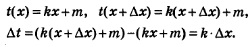
А теперь применим известный алгоритм из пяти шагов для отыскания производной.
1) Положим, ради удобства, f(кх+m) = h(х). Для фиксированного значения х имеем: h(х) = f(hх+m) = f(x).
2) В точке
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|