|
Гіпермаркет Знань>>Фізика і астрономія>>Фізика 11 клас>> Фізика: Вільні електромагнітні коливання. Перетворення енергії у коливальному контурі. Власна частота коливань
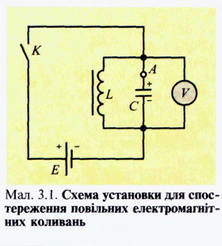
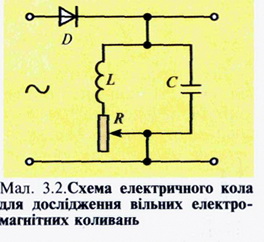
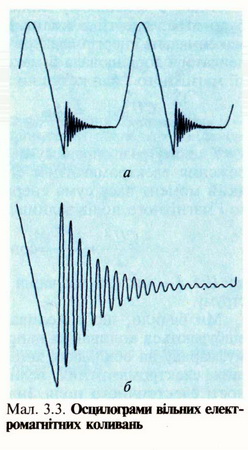
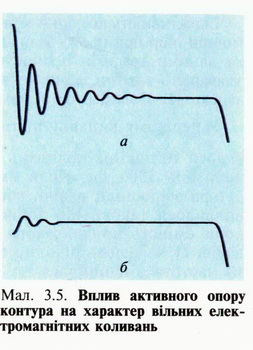
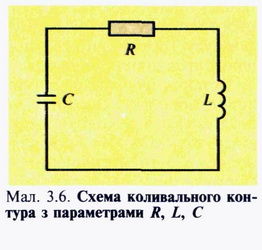
ВІЛЬНІ КОЛИВАННЯ В КОЛИВАЛЬНОМУ КОНТУРІ Найпростішим пристроєм, в якому досить просто можна спостерігати електромагнітні коливання, є електричне коло, що складається з котушки індуктивністю L та конденсатора ємністю С (мал. 3.1). Зрозуміло, що провідник, з якого виготовлено котушку, має й активний опір R, але спочатку ми ним нехтуватимемо. Щоб легко можна було спостерігати за змінами напруги на обкладках конденсатора, до яких під'єднано вольтметр V, коливання мають бути досить повільні. Тому в такому пристрої використовують котушку значної індуктивності (наприклад 25 Гн) і конденсатор великої ємності (1000—2000 мкФ). Вольтметр беруть з нульовою поділкою посередині шкали. Коли замкнути ключ К, то конденсатор С зарядиться від джерела постійного струму Е і вольтметр покаже напругу на його обкладках. Від'єднуємо джерело від досліджуваного кола. Вольтметр покаже наявність коливань напруги, які швидко припиняються. Значення і знак напруги на обкладках конденсатора змінюються, що засвідчує періодичне перезаряджання обкладок конденсатора. Отже, можна дійти висновку, що коли систему вивести зі стану рівноваги (зарядити конденсатор від стороннього джерела), то після від'єднання джерела в колі відбуватимуться коливання напруги U і пов'язаного з напругою простим співвідношенням заряду q = CU. Основними фізичними величинами, що характеризують коливальний контур (параметри контура), є його індуктивність, ємність та активний опір Проте оскільки напруга є енергетичною характеристикою електричного поля, й енерпю електричного поля конденсатора визначають за формулою то зі зміною напруги відбуваються також періодичні зміни енергії електричного поля конденсатора (аналогічно змінам потенціальної енергії пружини у разі виникнення гармонічних коливань тягаря на пружині). На який же інший вид енергії перетворюється енергія електричного поля конденсатора? Під час перезарядження обкладок конденсатора в котушці виникає струм, сила якого визначає енергію магнітного поля: Щоб упевнитись у правильності зробленого нами висновку про перетворення енергії, в точку А досліджуваного електричного кола (мал. 3.1) помістити амперметр, також з нульовою поділкою посередині шкали. Вимірювальні прилади покажуть, що коли напруга на обкладках конденсатора максимальна, то сила струму в колі дорівнює нулю, і навпаки, коли напруга дорівнює нулю, то сила струму максимальна. Отже, можна говорити про періодичні перетворення енергії електричного поля конденсатора на енергію магнітного поля котушки зі струмом і навпаки. Електричне коло, що складається з котушки і конденсатора, називають коливальним контуром, хоча, як побачимо, далі в таких колах не завжди можна спостерігати коливання. Досліджувані коливання швидко припиняються, що зумовлено витратами енергії на нагрівання провідників, перемагнічування феромагнітного осердя котушки, випромінювання частини енергії в простір у вигляді електромагнітних хвиль. Енергія електричного поля конденсатора де С — ємність конденсатора, U — напруга на обкладках конденсатора, a q — заряд на одній з його обкладок Енергія магнітного поля котушки (провідника) де L — індуктивність котушки (провідника), / — сила струму в ній Лише в ідеальному випадку, коли б не було втрат енергії в коливальному контурі, максимальна енергія електричного поля конденсатора дорівнювала б максимальній енергії магнітного поля котушки зі струмом: У цьому разі справджувався б закон збереження електромагнітної енергії, і в будь-який момент часу сума енергій електричного і магнітного полів залишалася б сталою: деU і І — миттєві значення напруги і сили струму. Ми бачили, що в коливальному контурі відбуваються коливання напруги, сили струму, заряду на обкладках конденсатора та інших електромагнітних величин (напруженості електричного поля, індукції магнітного поля тощо). Тепер потрібно встановити, якими параметрами коливального контуру визначаються період і частота коливань. Для цього можна поставити експеримент з використанням електронного осцилографа. Складемо електричне коло за схемою, наведеною на мал. 3.2. Досліджуване коло містить напівпровідниковий діод, який пропускає до контуру струм промислової частоти (50 Гц — 50 коливань за секунду) лише в один з півперіодів, тобто протягом 1100с. У другий півперіод струм через діод не проходить. Однак у перший півперіод конденсатор контуру зарядився, тому в другий півперіод він розряджатиметься через котушку і реостат, і в контурі виникатимуть затухаючі електромагнітні коливання. На екрані осцилографа можна спостерігати графік зміни напруги на обкладках конденсатора (мал. 3.3, а) — графік півперіоду змінного струму промислової частоти (половини синусоїди) і графік затухаючих коливань (мал. 3.3, б), який нас, власне, і цікавить. Ідеальним називають коливальний контур, у якому немає ніяких втрат електромагнітної енергії Тепер, коли ми знаємо, що затухаючі коливання відбуваються протягом 1100с, за допомогою ручок керування роботою осцилографа можемо одержати на екрані лише графік затухаючих коливань (див. мал. 3.3, б) і визначити їх частоту й період. За 1100с відбувалось 20 коливань. Отже, частота коливань — кількість коливань за одну секунду — дорівнює: Період коливань: Дослідимо залежність частоти коливань від ємності конденсатора в коливальному контурі. Зафіксуємо три послідовні фази експерименту (мал. 3.4, а, б, в). На першому з них наведено графік коливань для ємності конденсатора 0,25, на другому — 0,5 і на третьому — 1,0 мкФ. У першому випадку протягом 1100с відбулося 10 повних коливань. Отже, частота коливань 1000 Гц. Коли ємність конденсатора збільшили вдвічі, частота коливань виявилося такою, що дорівнює 700 Гц, а коли ємність конденсатора збільшили ше вдвічі (у 4 рази порівняно з початковою), то частота зменшилася до 500 Гц. З цих результатів можна зробити висновок: зі збільшенням ємності конденсатора вдвічі, частота коливань зменшується у При сталих індуктивності та активного опору контура період коливань у ньому У дослідах з котушками зручно їх індуктивність збільшувати внесенням у них феромагнітних осердь, щоб не змінювався їх активний опір, як при збільшенні кількості витків Далі аналогічно дослідимо залежність частоти коливань від індуктивності котушки. Відомо, що індуктивність котушки L залежить від кількості витків у ній, її конфігурації, а також від наявності в ній феромагнітного осердя. Яким же із зазначених способів зміни індуктивності варто скористатись у досліді? Конфігурацію котушки змінити досить складно. Збільшити кількість витків у котушці вдвічі досить просто, але при цьому зміниться й активний опір котушки і, можливо, саме він впливатиме на значення частоти. Тому збільшуватимемо індуктивність котушки внесенням в неї феромагнітного осердя. В момент внесення осердя індуктивність котушки зростає, а частота коливань зменшується. На мал. 3.4, б наведено фазу досліду, коли індуктивність котушки більша у 2 рази, ніж для випадку, зображеному на мал. 3.4, а, частота коливань тут 700 Гц. У міру подальшого збільшення індуктивності ще вдвічі (мал. 3.4, в) частота дорівнює 500 Гц. Зрозуміло, що тут маємо таку саму залежність, як і при збільшенні ємності конденсатора. Частота коливань виявляється обернено пропорційною кореню квадратному з індуктивності котушки: Тепер встановимо, як впливає значення активного опору контура на характер коливань у ньому. Активний опір контура можна змінювати за допомогою реостата або приєднанням до котушки послідовно резисторів з певними опорами (мал. 3.5, а, б — відповідно, резистори на 10 і 20 Ом). Дослід показує, що зі збільшенням значення активного опору контура амплітуда коливань швидко зменшується, коливання значно швидше припиняються. Однак активний опір на частоту коливань помітно не впливає (нижче побачимо, що такий вплив все-таки є). На практиці для визначення частоти коливань у коливальному контурі часто користуються формулою Томсона (1853 p.): де /— частота коливань, Гц; Т— період коливань, с; L — індуктивність, Гн; С — ємність, Ф. Частота і період електромагнітних коливань в ідеальних контурах визначаються за формулами Томсона Ці формули цілком придатні і для більшості випадків практики З останнього досліду можна зробити важливий висновок: не завжди в електричному колі, яке складається з котушки і конденсатора, можливі електромагнітні коливання. Якщо опір електричного кола досить значний, то після заряджання конденсатора він розрядиться через котушку зі значним опором. Однак при цьому енергія електричного поля конденсатора перетвориться на теплоту і конденсатор унаслідок явища самоіндукції не перезарядиться. Матиме місце так зване аперіодичне розряджання конденсатора. Встановимо умови, за яких коливання можливі, а за яких — ні. Однак для цього потрібно докладно проаналізувати явища в коливальному контурі з використанням математичного апарату. Уявімо собі коливальний контур, до складу якого входить конденсатор С, котушка L та активний опір R (мал. 3.6). Нехай у певний момент часу конденсатор зарядили до напруги U і від'єднали зовнішнє джерело живлення. Якби в електричному колі був лише резистор R, то струм протікав би лише доти, доки потенціали обкладок конденсатора не зрівнялися. Якщо ж у колі є котушка з індуктивністюL, то в той момент, коли потенціали обкладок конденсатора зрівняються, електрорушійна сила самоіндукції, що виникає в котушці при зміні сили струму в ній, підтримає струм, який зменшується, і відбудеться перезарядження обкладок конденсатора. Після цього струм у контурі йтиме у протилежному напрямку, конденсатор знову перезарядиться і т. д. Виникають електромагнітні коливання, які ми вже дослідили експериментально. Оскільки частина енергії втрачається, то коливання затухають і з часом припиняються зовсім. В електричних колах з індуктивністю, ємністю та активним опором електромагнітні коливання можуть і не виникнути при певних співвідношеннях між згаданими величинами (L, С, R) У реальних контурах (із втратами енергії) період електромагнітних коливань визначається за формулою: Ідеальними вважають контури, в яких немає втрат електромагнітної енергії. Для цього випадкуR = 0 і формула переходить у формулу Томсона, цілком придатну для більшості практичних випадків. Остання формула дає змогу зробити важливий висновок: за яких умов коливання в досліджуваному колі можливі. Значення періоду коливань має бути додатним числом і не може бути нескінченно великим. Тож у формулі знаменник має бути більшим за нуль. Отже, або Лише за цих умов коливання в колі можливі і коло можна вважати коливальним контуром. Якщо R = 0 (ідеальний контур), то формула Томсона Обов'язкова умова можливості виникнення вільних електромагнітних коливань Під час вільних коливань у контурі між напругою і силою струму встановлюється певне співвідношення, яке визначається параметрами контура. Сила струму в двох контурах за однакової амплітуди напруга може бути різною. Тому контур характеризують так званим хвильовим (або характеристичним) опором. Якщо знехтувати втратами енергії в контурі, то можна вважати, шо максимальне значення енергії магнітного поля котушки дорівнює максимальному значенню енергії електричного поля конденсатора: Звідси можна знайти співвідношення між амплітудою сили струму й амплітудою напруги: Вираз Щоб з'ясувати фізичний зміст характеристичного опору, розглянемо два контури, частоти власних коливань яких однакові, а конденсатори різних ємностей, наприклад С1< C2. Обидва конденсатори заряджаються до однакової напруги, але в першому контурі запас енергії Чим більший хвильовий (характеристичний) опір контура, тим менша сила струму в ньому за однакових інших умов ЗАПИТАННЯ
Планування уроків з фізики, відповіді на тести, завдання та відповіді по класам, домашнє завдання та робота з фізики для 11 класу
Зміст уроку
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: