|
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Задачи-1(11 класс)
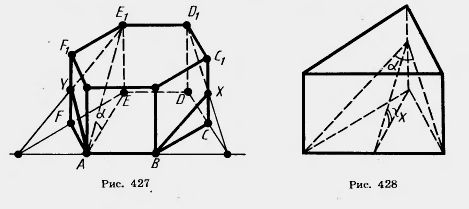
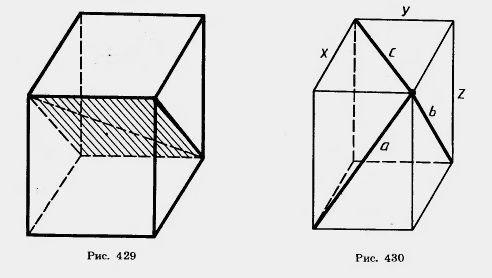
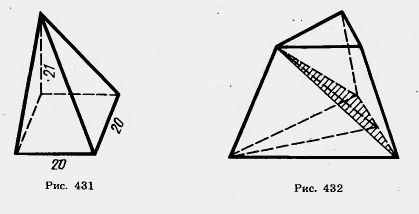
Задачи 1) отрезок АВ, если АА1=а, ВВ1 = b, А1В1=с и двугранный угол равен 2) двугранный угол 2. У трехгранного угла (аbс) двугранный угол при ребре с прямой, двугранный угол при ребре b равен 3. У трехгранного угла один плоский угол равен 4*. У трехгранного угла два плоских угла острые и равны а, а третий угол равен 5. Докажите, что сечение призмы, параллельное основаниям, равно основаниям. 6. Сколько диагоналей имеет n-угольная призма? 8. Постройте сечение четырехугольной призмы плоскостью, проходящей через три точки на боковых ребрах призмы. 9. У призмы одно боковое ребро перпендикулярно плоскости основания. Докажите, что остальные боковые ребра тоже перпендикулярны плоскости основания. 10. В прямой треугольной призме стороны основания равны 10 см, 17 см и 21 см, а высота призмы 18 см. Найдите площадь сечения, проведенного через боковое ребро и меньшую высоту основания. 11. Боковое ребро наклонной призмы равно 15 см и наклонено к плоскости основания под углом 30°. Найдите высоту призмы. 12*. В наклонной треугольной призме расстояния между боковыми ребрами равны 37 см, 13 см и 40 см. Найдите расстояние между большей боковой гранью и противолежащим боковым ребром. 13. Основанием призмы является правильный шестиугольник со стороной а, боковые грани — квадраты. Найдите диагонали призмы и площади ее диагональных сечений. 14*. В правильной шестиугольной призме, у которой боковые грани — квадраты, проведите плоскость через сторону нижнего основания и противолежащую ей сторону верхнего основания. Сторона основания равна а. Найдите площадь построенного сечения (рис. 427). 15. Через сторону нижнего основания правильной треугольной призмы проведена плоскость, пересекающая боковые грани по отрезкам, угол между которыми 16. В правильной четырехугольной призме через середины двух смежных сторон основания проведена плоскость, пересекающая три боковых ребра и наклоненная к плоскости основания под углом 18. В правильной четырехугольной призме площадь боковой грани равна Q. Найдите площадь диагонального сечения. 19*. Сторона основания правильной четырехугольной призмы равна 15, высота равна 20. Найдите кратчайшее расстояние от стороны основания до не пересекающей ее диагонали призмы (рис. 429). 20. В прямой треугольной призме все ребра равны. Боковая поверхность равна 12 м2. Найдите высоту. 21. Боковая поверхность правильной четырехугольной призмы 32 м2, а полная поверхность 40 м2. Найдите высоту. 22*. В наклонной призме проведено сечение, перпендикулярное боковым ребрам и пересекающее все боковые ребра. Найдите боковую поверхность призмы, если периметр сечения равен р, а боковые ребра равны I. 23. Расстояния между параллельными прямыми, содержащими боковые ребра наклонной треугольной призмы, равны 2 см, 3 см и 4 см, а боковые ребра 5 см. Найдите боковую поверхность призмы. 24. По стороне основания а и боковому ребру b найдите полную поверхность правильной призмы: 1) треугольной; 2) четырехугольной; 3) шестиугольной. 25. Плоскость, проходящая через сторону основания правильной треугольной призмы и середину противолежащего ребра, образует с основанием угол 45°. Сторона основания 1. Найдите боковую поверхность призмы. 26. У параллелепипеда три грани имеют площади 1 м2, 2 м2 и 3 м2. Чему равна полная поверхность параллелепипеда? 27. Известны углы, образуемые ребрами параллелепипеда, сходящимися в одной вершине. Как найти углы между ребрами, сходящимися в любой другой вершине? 28. Докажите, что отрезок, соединяющий центры оснований параллелепипеда, параллелен боковым ребрам. 29. В прямом параллелепипеде стороны основания 6 м и 8 м образуют угол 30°, боковое ребро равно 5 м. Найдите полную поверхность этого параллелепипеда. 30. В прямом параллелепипеде стороны основания 3 см и 8 см, угол между ними 60°. Боковая поверхность равна 220 см2. Найдите полную поверхность. 31. В прямом параллелепипеде стороны основания 3 см и 5 см, а одна из диагоналей основания 4 см. Найдите большую диагональ параллелепипеда, зная, что меньшая диагональ образует с плоскостью основания угол 60°. 32. Найдите диагонали прямого параллелепипеда, у которого каждое ребро равно а, а угол основания равен 60°. 33*. Боковое ребро прямого параллелепипеда 5 м, стороны основания 6 м и 8 м, а одна из диагоналей основания 12 м. Найдите диагонали параллелепипеда. 34. В прямом параллелепипеде боковое ребро 1 м, стороны основания 23 дм и 11 дм, а диагонали основания относятся как 2:3. Найдите площади диагональных сечений. 35. Найдите диагонали прямоугольного параллелепипеда по трем его измерениям: 1) 1, 2, 2; 2) 2, 3, 6; 3) 6, 6, 7. 36*. Ребро куба равно с. Найдите расстояние от вершины куба до его диагонали, соединяющей две другие вершины. 37. В прямоугольном параллелепипеде стороны основания 7 дм и 24 дм, а высота параллелепипеда 8 дм. Найдите площадь диагонального сечения. 38. Найдите поверхность прямоугольного параллелепипеда по трем его измерениям: 10 см, 22 см, 16 см. 39. Найдите боковую поверхность прямоугольного параллелепипеда, если его высота ft, площадь основания Q, а площадь диагонального сечения М. 40. Диагонали трех граней прямоугольного параллелепипеда, сходящиеся в одной вершине, равны а, b, с. Найдите линейные размеры параллелепипеда (рис. 430). 41. Основание пирамиды — равнобедренный треугольник, у которого основание равно 12 см, а боковая сторона 10 см. Боковые грани образуют с основанием равные двугранные углы, содержащие по 45°. Найдите высоту пирамиды. 43. Основанием пирамиды является правильный треугольник; одна из боковых граней перпендикулярна основанию, а две другие наклонены к нему под углом а. Как наклонены к плоскости основания боковые ребра? 44. В основании пирамиды лежит прямоугольный треугольник с гипотенузой a. Каждое боковое ребро образует с плоскостью основания угол 45. Основание пирамиды — прямоугольный треугольник с катетами 6 см и 8 см. Все двугранные углы при основании пирамиды равны 60°. Найдите высоту пирамиды. 46. Основание пирамиды — параллелограмм, у которого стороны 3 см и 7 см, а одна из диагоналей 6 см; высота пирамиды проходит через точку пересечения диагоналей, она равна 4 см. Найдите боковое ребро пирамиды. 47*. Основание пирамиды — ромб с диагоналями 6 м и 8 м; высота пирамиды проходит через точку пересечения диагоналей ромба и равна 1 м. Найдите боковую поверхность пирамиды. 48. Основание пирамиды — равнобедренный треугольник со сторонами 40 см, 25 см и 25 см. Ее высота проходит через вершину угла, противолежащего стороне 40 см, и равна 8 см. Найдите боковую поверхность пирамиды. 49. Основание пирамиды — квадрат, ее высота проходит через одну из вершин основания. Найдите боковую поверхность пирамиды, если сторона основания равна 20 дм, а высота 21 дм (рис. 431). 50. Постройте сечение пирамиды плоскостью, проходящей через вершину пирамиды и две данные точки на ее основании. 51. Постройте сечение треугольной пирамиды плоскостью, проходящей через сторону основания пирамиды и данную точку на противолежащем ребре. 52. Постройте сечение четырехугольной пирамиды плоскостью, проходящей через сторону основания и точку на одном из боковых ребер. 53. У четырехугольной усеченной пирамиды стороны одного основания равны 6, 7, 8, 9 см, а меньшая сторона другого основания равна 5 см. Найдите остальные стороны этого основания. 54. Боковое ребро пирамиды разделено на четыре равные части и через точки деления проведены плоскости, параллельные основанию. Площадь основания равна 400 см^. Найдите площади сечений. 55. Высота пирамиды равна 16 м. Площадь основания равна 512 м2. На каком расстоянии от основания находится сечение, параллельное ему, если площадь сечения 50 м2? 56. В правильной треугольной пирамиде с высотой h через сторону основания а проведена плоскость, пересекающая противолежащее боковое ребро под прямым углом. Найдите площадь сечения. 57. Высота правильной четырехугольной пирамиды равна 7 см, а сторона основания 8 см. Найдите боковое ребро. 58. В правильной четырехугольной пирамиде плоский угол при вершине равен а. Найдите двугранный угол х при основании пирамиды. 59. По данной стороне основания а и боковому ребру b найдите высоту правильной пирамиды: 1) треугольной; 2) четырехугольной; 3) шестиугольной. 60.По данной стороне основания а и высоте b найдите апофему правильной пирамиды: 1) треугольной; 2) четырехугольной; 3) шестиугольной. 61.По стороне основания а и высоте h найдите полную поверхность правильной пирамиды: 1) треугольной; 2) четырехугольной; 3) шестиугольной. 62. Найдите полную поверхность правильной шестиугольной пирамиды, если ее боковое ребро а, а радиус окружности, вписанной в основание, r. 63. В правильной четырехугольной пирамиде боковая поверхность равна 14,76 м , а полная поверхность Найдите сторону основания и высоту пирамиды. 64. По стороне основания о найдите боковую поверхность правильной четырехугольной пирамиды, у которой диагональное сечение равновелико основанию. 65. Найдите боковую поверхность пирамиды, если площадь основания Q, а двугранные углы при основании 66. Найдите двугранные углы при основании правильной пирамиды, у которой площадь основания равна Q, а боковая поверхность S. 68. В правильной четырехугольной пирамиде найдите сторону основания, если боковое ребро равно 5 см, а полная поверхность 16 см2. 69. Докажите, что боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему. 70. Высота правильной четырехугольной усеченной пирамиды равна 7 см. Стороны оснований равны 10 см и 2 см. Найдите боковое ребро пирамиды. 71. Стороны оснований правильной усеченной треугольной пирамиды 4 дм и 1 дм. Боковое ребро 2 дм. Найдите высоту пирамиды. 72. В правильной четырехугольной усеченной пирамиде высота равна 2 см, а стороны оснований 3 см и 5 см. Найдите диагональ этой пирамиды. 73. Стороны оснований усеченной правильной треугольной пирамиды 2 см и 6 см. Боковая грань образует с большим основанием угол 60°. Найдите высоту. 74. В правильной усеченной треугольной пирамиде сторона большего основания a, сторона меньшего — b. Боковое ребро образует с основанием угол 45°. Найдите площадь сечения, проходящего через боковое ребро и ось пирамиды'. 75. Высота правильной четырехугольной усеченной пирамиды равна 4 см. Стороны оснований равны 2 см и 8 см. Найдите площади диагональных сечений. 76. В правильной треугольной усеченной пирамиде сторона нижнего основания 8 м, верхнего — 5 м, а высота 3 м. Проведите сечение через сторону нижнего основания и противоположную вершину верхнего основания. Найдите площадь сечения и двугранный угол между сечением и нижним основанием (рис. 432). 77. В правильной четырехугольной усеченной пирамиде стороны оснований 8 м и 2 м. Высота равна 4 м. Найдите полную поверхность. 78. Найдите полную поверхность правильной усеченной пирамиды: 1) треугольной; 2) четырехугольной; 3) шестиугольной, если высота h, а стороны оснований а и b. 79. Докажите, что центры граней куба являются вершинами октаэдра, а центры граней октаэдра являются вершинами куба. Ось правильной усеченной пирамиды совпадает с осью соответствующей полной пирамиды. 80. Докажите, что концы двух непараллельных диагоналей противолежащих граней куба являются вершинами тетраэдра. 81. Найдите двугранные углы правильного тетраэдра. 82*. Найдите двугранные углы октаэдра. 83. Какие плоскости симметрии имеет правильный тетраэдр? 84*. Сколько плоскостей симметрии у правильного октаэдра, додекаэдра и икосаэдра?
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: