|
Гипермаркет знаний>>Математика>>Математика 10 класс>>Математика: Задачи-2(10 класс)
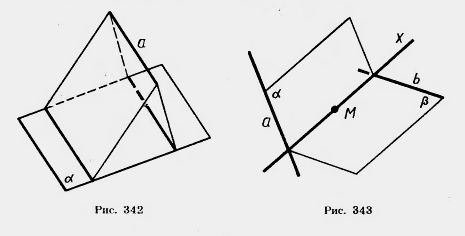
2. Можно ли через точку С, не принадлежащую скрещивающимся прямым а и b, провести две различные прямые, каждая из которых пересекает прямые а и b? Объясните ответ. 3. Докажите, что все прямые, пересекающие две данные параллельные прямые, лежат в одной плоскости. 4. Прямые а и b пересекаются. Докажите, что все прямые, параллельные прямой b и пересекающие прямую а, лежат в одной плоскости.
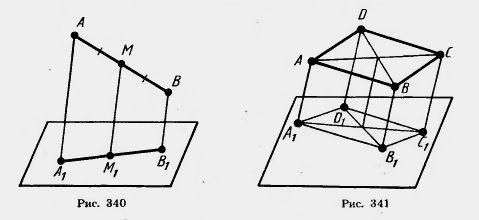
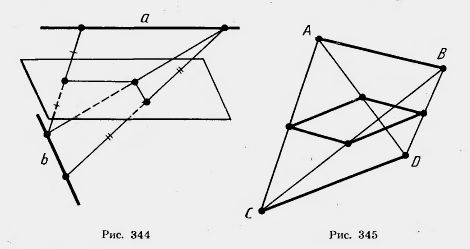
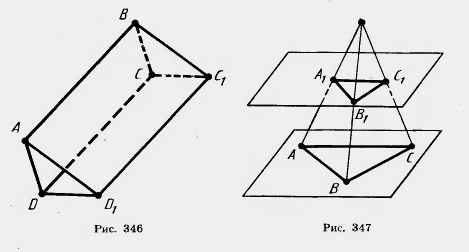
1) АА1=5 м, ВВ1 = 7 м; 2) АА1=3,6 дм, ВВ1 =4,8 дм; 6*. Решите задачу 5, если АВ пересекает плоскость. 7. Через конец А отрезка АВ проведена плоскость. Через конец В и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Найдите длину отрезка ВВ1, если: 1) CC1 = 15 см, АС:ВС = 2:3; 3) АВ=6 см, АС:CC1= 2:5; 4) АС = а, ВС = b, CC1=с. 1) АА1=2 м, BB1 = 3 м, CC1=8 м; 2) AA1 = 4 м, BBB1 = 3 м, CC1 = l м; 3) AA1= а, BB1 = b, CC1=с. 9. Прямые а и b не лежат в одной плоскости. Можно ли провести прямую с, параллельную прямым а и b? 10. Точки А, В, С, D не лежат в одной плоскости. Докажите, что прямая, проходящая через середины отрезков АВ и ВС, параллельна прямой, проходящей через середины отрезков AD и CD. 11. Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма (вершины пространственного четырехугольника не лежат в одной плоскости). 12*. Даны четыре точки А, В, С, D, не лежащие в одной плоскости. Докажите, что прямые, соединяющие середины от резков АВ и CD, АС и BD, AD и ВС, пересекаются в одной точке. 13. Дан треугольник ABC. Плоскость, параллельная прямой АВ, пересекает сторону АС этого треугольника в точке A1, а сторону ВС — в точке В1. Найдите длину отрезка А1 В1, если: 1) АВ = 15 см, АА1:АС = 2:3; 2) АВ = 8см, АА1:А1С = 5:3; 3) B1C = 10 см, АВ:ВС = 4:5; 4) АА1=а, АВ=b, А1С = с. 15. Докажите, что плоскость, пересекающая одну из двух параллельных прямых, пересекает и другую. 16. Докажите, что через любую из двух скрещивающихся прямых можно провести плоскость, параллельную другой прямой. 17. Докажите, что если две плоскости, пересекающиеся по прямой а, пересекают плоскость а по параллельным прямым, то прямая а параллельна плоскости ее (рис. 342). 18. Докажите, что прямая,пересекающая одну из двух параллельных плоскостей, пересекает и другую. 19. Докажите, что через две скрещивающиеся прямые можно провести параллельные плоскости. 20. Через данную точку пространства проведите прямую, пересекающую каждую из двух скрещивающихся прямых (рис. 343). Всегда ли это возможно? 21*. Докажите, что геометрическое место середин отрезков с концами на двух скрещивающихся прямых есть плоскость, параллельная этим прямым (рис. 344). 22. Даны четыре точки А, В,С и D, не лежащие в одной плоскости. Докажите, что любая плоскость, параллельная прямым АВ и CD, пересекает прямые АС, AD, BD и ВС в вершинах параллелограмма (рис. 345). 24. Плoскости 25. Докажите, что все прямые, проходящие через данную точку параллельно данной плоскости, лежат в одной плоскости. 26. Через данную точку проведите плоскость, параллельную каждой из двух пересекающихся прямых. Всегда ли это возможно? 27. Параллелограммы ABCD и ABC1D1 лежат в разных плоскостях. Докажите, что четырехугольник CDD1C1 тоже параллелограмм (рис. 346). 28. Через вершины параллелограмма ABCD, лежащего в одной
29. Через вершины треугольника ABC, лежащего в одной из двух параллельных плоскостей, проведены параллельные прямые, пересекающие вторую плоскость в точках А1В1С1. Докажите равенство треугольников ABC и А1В1С1. 30. Три прямые, проходящие через одну точку, пересекают данную плоскость в точках А, В, С, а параллельную ей плоскость в точках А,, В\, С\. Докажите подобие треугольников ABC и А1В1С1 (рис. 347). 31. Докажите, что если четыре прямые, проходящие через точку А, пересекают плоскость
33*. Даны две параллельные плоскости 34*. Точка А лежит вне плоскости 35*. Даны три параллельные плоскости 36. Даны четыре параллельные прямые. Докажите, что если какая-нибудь плоскость пересекает эти прямые в вершинах параллелограмма, то любая плоскость, не параллельная данным прямым, пересекает их в вершинах некоторого параллелограмма. 37. Дана параллельная проекция треугольника. Как построить проекции его медиан? 38. Дана параллельная проекция треугольника. Чем изобразится проекция средней линии треугольника? 39. Может ли при параллельном проектировании параллелограмма получиться трапеция? Объясните ответ. 40. Может ли проекция параллелограмма при параллельном проектировании быть квадратом? 41. Докажите, что параллельная проекция центрально-симметричной фигуры также является центрально-симметричной фигурой. 42*. Дана параллельная проекция окружности и ее диаметра (рис. 349). Как построить проекцию перпендикулярного диаметра?
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: