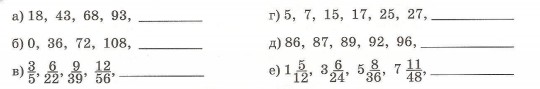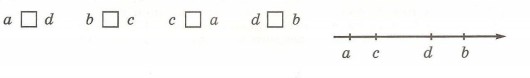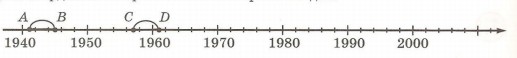|
Гипермаркет знаний>>Математика>>Математика 4 класс>> Задачи на повторение (4 класс)

1. Найди закономерность и продолжи ряд чисел:
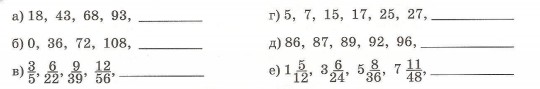
2. Запиши следующие три числа в последовательности:
50, 505, 5 050, 50 505, ---------------------, -------------------, ------------------.
Прочитай записанные числа. Сколько цифр используется для их записи?
3. Прочитай число: 75 860 000 706.
а) Сколько в нем классов? Назови их. Какие еще названия классов ты знаешь?
б) Сколько разрядов в каждом классе и как они называются?
в) Какая цифра стоит в разряде сотен миллионов данного числа? Сколько в нем всего сотен миллионов?
г) Что означает цифра 7 в записи этого числа?
4. Запиши цифрами числа:
а) восемьсот четыре тысячи двести;
б) тридцать тысяч девятьсот девять;
в) шесть миллионов семьдесят три;
г) пятнадцать миллиардов пятьдесят шесть тысяч;
д) наибольшее восьмизначное число;
е) наименьшее десятизначное число.
5. Запиши цифрами и прочитай числа:
а) 840 тыс. = ---------------- в) 32 млн. = ---------------------------
б) 5076 тыс. = --------------- г) 124 045 млн. = -------------------------
6. Запиши и прочитай числа, представленные в виде суммы разрядных слагаемых. Назови отсутствующие разряды в записи этих чисел.
а) 200 + 10 + 4 = ---------------
б) 800 + 90 ----------------------
в) 5000 + 600 + 2 = ---------------------
г) 18 000 + 30 + 1 = --------------------
д) 100 000 + 4000 + 300 + 40 + 7 = ----------------
е) 8 000 000 + 60 000 + 200 + 50 = ------------------------
7. Представь числа в виде суммы разрядных слагаемых: а) 428; в) 950; г) 3 075; д) 25 002; е) 780 430; ж) 6 290 056.
8. а) Вырази число 5609 в десятках и единицах; в сотнях и единицах; в тысячах и единицах.
б) Вырази 5609 мм в сантиметрах и миллиметрах; в дециметрах и миллиметрах; в метрах и миллиметрах.
в) Вырази 5609 с в минутах и секундах; в часах, минутах и секундах.
9. а) Запиши цифры римской нумерации, обозначающие числа:
один
| пять
| десять
| пятьдесят
| сто
| пятьсот
| тысяча
|
|
|
|
|
|
|
|
|
Как записываются числа в этой нумерации?
б) Запиши арабскими цифрами числа:
XIV, XXI, CXLVI, CCCLXIX, DCXII, MCDVIII.
в) Запиши римскими цифрами числа:
25, 74, 48, 83, 316, 532, 1249.
10*.
Запиши в египетской нумерации числа 25, 74, 316, 532.
11*. 
Запиши в древнегреческой нумерации числа 25, 74, 316, 532.
12*. Как обозначали числа древние вавилоняне? Запиши а вавилонской нумерации числа 25, 74, 316, 532. Запиши эти числа в древнерусской нумерации (№ 14, стр. 12).
13. Сравни числа:
5630 ... 5603
24 239 ... 24 293
333 333 ... 88 888
7 600 000 ... 67 000 000
875 316 049 ... 875 310 699
1 093 284 915 ... 10 000 000 100
14. В числах вместо некоторых цифр записаны звездочки. Можно ли сравнить эти числа?
3* ... 1 **
8 ** ... 5 * *
7**8 * ... 7**2*
15. Запиши для каждого неравенства множество цифр, при подстановке которых вместо звездочки получается верное высказывание:
* 64 < 364
52 * 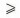 529 529
46 * 1 > 4671
5*68 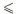 5168 5168
340 < 3 * 4 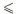 372 372
125 .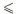 *25 < 400 *25 < 400
16. Является ли число 4 решением неравенства 9 - х < 3? Докажи. Приведи пример неравенства, решением которого является это число.
17. Найди пересечение множеств натуральных решений неравенств 7 < х 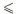 12 и у - 5 < 6. Построй диаграммы Венна этих множеств. 12 и у - 5 < 6. Построй диаграммы Венна этих множеств.
18. Найди объединение множеств натуральных решений неравенств 12 - х 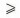 7 и 3 7 и 3 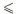 у < 8. Построй диаграммы Венна этих множеств. у < 8. Построй диаграммы Венна этих множеств.
19. Пользуясь деревом возможностей, определи, сколько можно составить четырехзначных чисел с цифрой тысяч 1 или 2, цифрой сотен 0, 4 или 7, цифрой десятков 5 или 3 и цифрой единиц 8 или 9. Найди произведение наибольшего и наименьшего из этих чисел.
20. Какая из величин больше и на сколько:
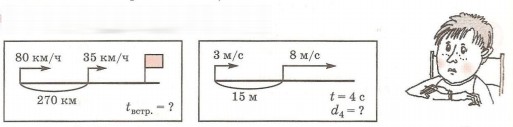
а) 6 км 48 м или 752 м;
б) 4 дм 3 мм или 96 см;
в) 5 мин или 400 с;
г) 2 сут. 45 мин или 23 ч 58 мин;
д) 8 т 6 ц 7 кг или 2989 кг;
е) 52 ц или 520 000 г;
ж) 7 м2 3 дм2 или 78 дм2 62 см2;
з) 916 мм3 или 9 см3 16 мм3?
21. Какая из величин меньше и во сколько раз:
а) 2 км 10 м или 402 м;
б) 35 мм или 14 м;
в) 1 ч или 45 с;
г) 8 сут. 8 ч или 800 ч;
д) 3 т 72 кг или 3 ц 84 кг;
е) 28 ц или 28 000 000 г;
ж) 2 м2 40 см2 или 33 дм2 40см2;
з) 125 мм3 или 40 см3?
22. Запиши высказывание в виде равенства тремя разными способами:
а) а на 7 больше, чем b ----------- -------------- --------------
б) c в 5 раз больше, чем d ----------- -------------- --------------
в) k на 4 меньше, чем n ----------- -------------- --------------
г) x в 9 раз меньше, чем у ----------- -------------- --------------
23. В школе 25 классов, в каждом из которых от 30 до 40 учеников. Пусть х — число учеников в классе. Запиши оценку значений переменной X в виде двойного неравенства. Какая из границ (верхняя или нижняя) точнее указывает примерное число учеников в классе, если в школе 814 учеников? 964 ученика?
24. По каким признакам можно классифицировать фигуры на рисунке? Разбей эти фигуры на части по форме и напиши соответствующие буквенные и числовые равенства. Отметь в каждом равенстве части и целое.
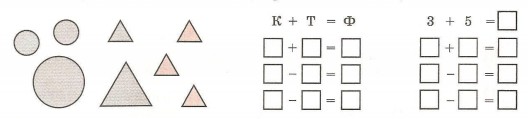
Что значит — сложить? Что значит — вычесть? Объясни, пользуясь установленными равенствами, как выполнить проверку сложения и вычитания.
25. Вставь в "окошки" пропущеные цифры и сделай проверку:

26. Прочитай выражения и найди их значения. Сделай проверку.
а) 56 926 049 + 2 739 487 958;
б) 30 720 034 851 - 6 087 336 257;
в) 814 638 572 467 + 46 274 579 455;
г) 497 730 460 002 - 98 790 873 256.
27. Найди и отметь в уравнениях части и целое. Реши уравнения с комментированием по компонентам действий. Сделай проверку.
а) х - 385 = 4615;
б) 749 + у = 8008;
в) а + 847 = 2034;
г) 6220 - d = 576;
д) k - 795 = 453 750;
е) 102 050 - b = 9564.
28. Расшифруй имя известного древнегреческого математика, расположив ответы примеров в порядке убывания:

29. Во время выборов в городе за одного из трех кандидатов проголосовало 34 026 избирателей, за второго — на 5847 избирателей больше, чем за первого, а за третьего — на 2685 избирателей меньше, чем за второго. Сколько человек участвовало в голосовании? Сколько человек не пришло на избирательные участки, если всего в этом городе по спискам 206 315 избирателей?
30. На овощной базе было 2350 ц капусты. В первый день с базы вывезли 384 ц капусты, что на 46 ц меньше, чем вывезли во второй день. В третий день капусты вывезли на 278 ц меньше, чем в первые два дня вместе. Сколько капусты еще осталось на базе?
31. Как изменяется сумма при увеличении и уменьшении слагаемых? Как изменяется разность при изменении компонент вычитания? Сравни выражения:
а + 39 ... а + 90
46 + b ... b + 46
c - 75 ... с - 57
84 - d ... 54 - d
66 - k ... 222 - k
n - 499 ... n - 500
32. Запиши оценку выражения в виде двойного неравенства. Какая из границ (верхняя или нижняя) меньше отличается от точного значения выражения?
а) 824 + 249; в) 743 - 518; д) 2637 + 5575;
б) 627 + 982; г) 906 - 367; е) 8351 - 4786.
33. Не выполняя вычислений, объясни почему действие выполнено неверно:
а) 483 + 315 = 598; в) 5354 + 5623 = 10 971;
б) 914 - 639 = 873; г) 7384 - 2548 = 1836.
34. координатной прямой обозначь деления шкалы числами удобным спо-собом и построй точки:

35. На сколько единиц и в какую сторону надо сместиться по координатной прямой, чтобы из точки А (16) попасть в точку с координатой: а) 14; б) 22; в) 12; г) 6; д) 21; е) 0; ж) 16?
36. Сравни числа, пользуясь их изображением на координатной прямой:
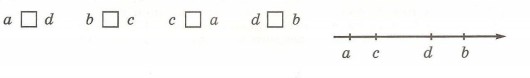
37. Найди длину отрезка АВ, если
а) А (34), В (60);
б) А (89), В (132):
в) А (7512), В (10 000).
38. На координатной прямой отмечено время в годах:
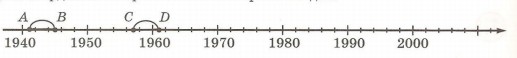
Точки обозначают следующие события:
А — начало Великой Отечественной войны;
В — взятие Берлина Советской армией;
С — запуск первого искусственного спутника Земли;
D — полет первого космонавта Ю. А. Гагарина.
Дугой АВ отмечен период Великой Отечественной войны, а дугой CD — промежуток времени от запуска первого искусственного спутника до полета первого космонавта.
Обозначь на этом рисунке точкой Е год твоего рождения, точкой F — год твоего поступления в школу. Дугой ЕК отметь промежуток времени твоей жизни от рождения до настоящего времени, а дугой FM — промежуток времени обучения в школе от поступления до окончания (в будущем).
39. Запиши выражения удобным способом и найди их значения:
а) 2085 + 2085 + 2085 + 2085 + 2085 + 2085 + 2085 + 2085;
б) 316 + 316 + 316 + 316 +9407 + 9407 + 9407 + 9407 + 9407;
в) 52 078 + 52 078 + 52 078 + 69 + 69 + 69 + 69 + 69 + 69 + 69.
Что значит — умножить число а на число Ь? Объясни целесообразность замены действия сложения одинаковых слагаемых действием умножения.
40. а) Найди сумму 52 слагаемых, каждое из которых равно 675.
б) Найди произведение чисел 16 700 и 408.
в) Увеличь число 361 400 в 90 раз.
41. Прочитай выражения разными способами. Сделай прикидку и найди их значения.
а) 8019 • 906; б) 753 000 • 700; в) 60 280 • 1004.
42. Перемножая числа 218 и 409, Олег получил в ответе 89 162, а Митя — 10 682, Кто из ребят допустил ошибку? В чем его ошибка?
43. Перемножая числа 31200 и 250, Ира получила в ответе 780 000, а Даша — 7 800 000. Кто из них ошибся? В чем ошибка?
44. Из одного кубического метра древесины можно изготовить 165 км искусственного волокна, а из него можно изготовить 1500 м ткани или 4000 пар чулок. Сколько искусственного волокна, ткани или чулок можно изготовить из 12 м3 древесины?
45. Заполни пустые клетки и запиши подходяпдие операции:

Какие арифметические операции обратны друг другу?
46. Найди сходство и отличие двух задач и сопоставь их решения на схемах:
а) 18 мячей разложили поровну в 3 коробки. Сколько мячей в каждой коробке?
б) 18 мячей разложили в коробки по 3 мяча в каждую. Сколько получилось коробок?
Что значит — разделить число а на число Ь? Какие два вида деления ты знаешь?
47. По рисунку составь четыре равенства и объясни их геометрический смысл. Отметь в каждом равенстве компоненты действий, соответствующие сторонам и площади прямоугольника.

Объясни, пользуясь установленными равенствами, как сделать проверку умножения и деления?
48. а) Раздели число 288 600 на 74 равные части.
б) Сколько раз число 283 содержится в числе 172 347?
в) Найди частное чисел 387 100 и 395.
г) Произведение двух множителей равно 375 300. Один из множителей равен 75. Найди второй множитель.
д) Во сколько раз 1 002 560 больше, чем 482?
е) Кратно ли число 503 232 числу 67?
ж) Является ли число 2405 делителем числа 163 540?
49. Прочитай выражения разными способами. Сделай прикидку и найди их значения.
а) 3 150 100 : 5; б) 4 413 920 : 49; в) 2 292 160 : 754.
50. Найди в уравнениях компоненты действий, соответствующие сторонам и площади прямоугольника. Реши уравнения с комментированием по компонентам действий и сделай проверку:
а) х • 80 = 28 320;
б) у : 204 = 352;
в) 20 640 : t = 645.
51. Вставь в "окошки" пропущеные числа и сделай проверку:
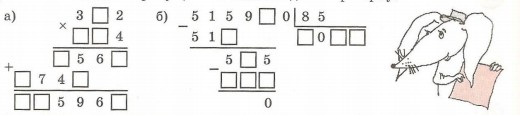
52. Сделай прикидку и выполни действия. Расположи ответы примеров в порядке возрастания, и ты узнаешь имя знаменитого древнегреческого математика.

53. Как изменяется произведение при увеличении и уменьшении множителей? Как изменяется частное при изменении компонент деления? Сравни выражения:
а • 74 ... 74 • а 168 : с ... 186 : с х • 7 + х • 5 ... х • 9 + х
980 : b ... 909 : b d : 356 ... d : 358 (m + n) • 3 ... m + n • 3
54. Запиши оценку выражения с помощью двойного неравенства. Какая из границ (верхняя или нижняя) меньше отличается от точного значения выражения?
а) 570 • 902; в) 315 514 : 361; д) 3509 • 9070;
б) 625 • 127; г) 743 700 : 925; е) 802 494 : 386.
55. Не выполняя вычислений, объясни, почему действие выполнено неверно:
а) 358 • 82 = 9356; в) 452 672 : 643 = 74; д) 8196 • 532 = 46 272;
б) 287 • 38 = 10 904; г) 214 240 : 412 = 502; е) 173 272 : 968 = 178.
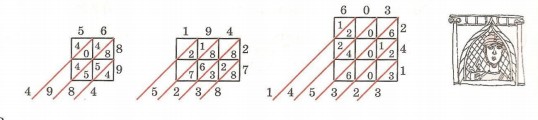
56*. В IX веке нашей эры арабский математик Мухаммед ибн Муса ал-Хорезми придумал способ умножения натуральных чисел, который называют методом решетки. Рассмотри примеры умножения чисел этим методом и найди соответствующий вычислительный алгоритм. Выполни умножение двух произвольных натуральных чисел в столбик и методом решетки. Какой из этих способов вычисления тебе нравится больше?
56 • 89 = 4984 194 • 27 = 5 238 603 • 241 - 145 323
57. Печенье упаковали в пачки по 250 г. Пачки сложили в ящик в 4 слоя. Каждый слой имеет 5 рядов по 6 пачек в каждом. Какова масса сложенного в ящик печенья?
58. Уголь возили на 4 машинах. Каждая из них сделала по 9 рейсов, привозя каждый раз по 2400 кг угля. Этот уголь расходовали поровну в течение 180 дней. Сколько килограммов угля расходовали ежедневно?
59. В куске было 20 м ткани. От него отрезали ткань на 3 юбки и 2 платья. На юбку идет по 1 м 80 см ткани, а на платье — 2 м 60 см. Сколько ткани еще осталось в куске?
60. С первой яблони собрали 36 кг яблок, со второй яблони — на 8 кг больше, чем с первой, а с третьей — в 2 раза меньше, чем со второй. Сколько ящиков потребуется для укладки всех яблок, если в один ящик умещается 10 кг яблок?
61. С одного поля собрали 160 ц картофеля, со второго поля — в 2 раза больше, чем с первого, а с третьего — на 60 ц меньше, чем с обоих полей вместе. Половину всего картофеля разложили в мешки по 50 кг в каждый и увезли их поровну на 15 машинах. Сколько мешков положили на каждую машину?
62. а) Из 10 м ткани получается 3 рубашки. Сколько таких рубашек можно сшить из 50 м этой ткани?
б) Из 100 л молока получается 4 кг масла. Сколько масла получится при переработке 6000 л молока?
63. Двум классам поручено расчистить школьный каток, длина которого 32 м, а ширина 20 м. В одном классе 42 ученика, а в другом — 38 учеников. Сколько квадратных метров придется на каждый класс, если распределить работу по числу учеников?
64. Реши уравнения с комментированием и сделай проверку:
а) (24 -х) • 5 - 32 = 48; в) 200 - (48 : t) • 45 = 20;
б) 720 : (у : 7 + 80) = 6; г) (у • 40 + 60) : 3 = 140.
65. Найди из приведенных примеров "лишний". Запиши в остальных примерах ответ и объясни, как выполняют действия с О и 1. Соответствующие правила запиши в общем виде.
0 + 23 = ...
75 - 0 = ...
46 - 46 = ...
58 • 0 = ...
1 • 39 = ...
74 : 1 = ...
25 : 25 = ...
0 : 16 = ...
28 : 0 = ...
0 • 0 = ...
0 • 1 = ...
0 : 1 = ...
66. Составь программу действий и вычисли:
а) 758 : 758 + (819 • 0 + 5) • (12 - 0) + 0 : 3509;
б) (82 : 82) • 15 + (8064 : 1 - 8064) • 472 + 29 • 1.
Какие правила о порядке выполнения арифметических действий использовались для решения этих примеров?
67. Найди значения выражений:
а) 7 740 : 86 • 35 + 2 000 : 8 - (5 760 : 90) • 52 + 38 430 : 7;
б) 54 200 - 49 • 76 - (24 792 + 5 874) : (207 - 169) + 705 • 108 : 30;
в) (32 999 + 62 111) : 1 - (508 • 45 + 4 544 • 1) : 34 - (10 000 - 37 • 196);
г) 1 536 300 : 270 • (56 484 : 523) - (7125 - 0 : 4726) • 248 : 62 + 3 005 • 0.
68. Приведи примеры величин, связанных зависимостью а = b • с. Запиши формулы:
а) пути -------------
б) работы ---------------
в) стоимости ----------------
г) площади прямоугольника -------------------------------
Придумай задачи об этих величинах, которые решаются так:
32 • 3 28 - 5 • 4 (18:2) • 4 64 • 5 - 25 • 6
240 : 80 60 : 3 - 72 : 4 225 : (90 : 2) 18 • 2 + 6 • 3
69. "Блиц-турнир".
а) Пешеход прошел путь а км за 5 ч, а велосипедист проехал его за 2 ч. Во сколько раз скорость пешехода меньше скорости велосипедиста?
б) Вася читает в час b страниц, а его младшая сестра — на 8 страниц меньше. На сколько быстрее своей сестры Вася прочитает книгу в c страниц?
в) За несколько шоколадок ценой по d р. заплатили x р., а за столько же пряников заплатили у р. Сколько стоил один пряник?
г) Два опытных участка прямоугольной формы имеют одинаковую площадь. Длина первого участка равна а м, а его ширина b м. Какова ширина второго участка, если его длина превышает длину первого участка на 7 м?
70. а) Автомобиль ехал 3 ч со скоростью 85 км/ч, следующие 2 ч он снизил скорость на 15 км/ч, а в последние 4 ч увеличил ее до 90 км/ч. Какое расстояние проехал автомобиль за все время движения?
б) Поезд должен пройти 1060 км за 14 ч. Первые 420 км он шел со скоростью 70 км/ч. С какой скоростью он должен идти оставшийся путь, чтобы прибыть в пункт назначения вовремя?
71. а) Библиотеке нужно переплести 2 700 книг. Одна мастерская может переплести эти книги за 15 дней, а вторая — за 30 дней. За сколько дней закончат работу эти мастерские, работая вместе?
б) Бассейн вмещает 3600 м^ воды. Он наполняется двумя трубами, включенными одновременно, за 12 ч, а одной первой трубой — за 20 ч. На сколько быстрее наполнит бассейн одна первая труба, чем одна вторая?
72. Для хоровой студии купили одинаковое число блузок и юбок, всего на сумму 2 тыс. 660 р. Юбка стоит 50 р., а блузка — 45 р. Сколько денег заплатили за все юбки?
73. Два огорода имеют форму прямоугольника. Плогцадь первого огорода равна 375 м2, что на 225 м2 меньше площади второго огорода. Длина первого огорода равна 25 м, а длина второго огорода в 2 раза больше. Па сколько метров ширина второго огорода меньше, чем ширина первого огорода?
74. а) Один мастер работал 3 ч, а второй — 5 ч. Вместе они сделали 120 деталей. Сколько деталей сделал каждый, если они работали с одинаковой производительностью?
б) В колхозе на одной пасеке 85 ульев, а на другой 55 ульев. С первой пасеки сняли на 1620 кг меда больше, чем со второй. Сколько килограммов меда сняли с каждой пасеки, если с каждого улья получали меда поровну?
75. Как называются свойства сложения и умножения, записанные в рамке? Объясни их смысл. Используя эти свойства, найди значение выражения удобным способом:
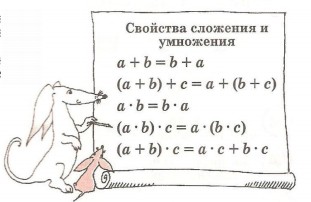
а) 32 + 34 + 36 + 38;
б) 5 + 183 + 295 + 17;
в) 2 • 7 • 5 • 9 • 2 • 5;
г) 25 • 49 • 4 • 5 • 20;
д) 56 • 29 + 71 • 56.
Какие еще свойства арифметических действий ты знаешь?
76. Запиши формулу деления с остатком. Объясни, пользуясь формулой, как при делении с остатком выполняется проверка результата.
Выполни деление и сделай проверку:
45 243 : 5 24 975 : 32 257 992 : 847 119 370 : 20
24 062 : 8 222 710 : 73 144 055 : 496 5 521 400 : 600
77. а) Найди по формуле объем прямоугольного параллелепипеда, если его измерения равны 15 см, 12 см, 24 см.
б) Объем комнаты равен 72 мЗ. Найди высоту комнаты, если ее длина равна 6 м, а ширина 4 м.
в) Сарай, имеющий форму прямоугольного параллелепипеда, заполнен сеном. Длина сарая 10 м, ширина 8 м, а высота 3 м. Определи массу сена в сарае, если масса 10 м3 сена равна 6 ц.
78*. Найди объем прямоугольного параллелепипеда, если две его грани площадью 48 см2 и 120 см2 имеют общее ребро длиной 8 см.
79. Как найти скорость сближения или скорость удаления двух объектов, если они движутся: а) навстречу друг другу; б) вдогонку; в) в противоположных направлениях; г) с отставанием? В каких случаях произойдет встреча? Запиши формулу одновременного движения.
80. Два катера плывут навстречу друг другу. Скорость первого катера 18 км/ч, а скорость второго катера на 6 км/ч больше. Сейчас между ними 168 км. На каком расстоянии друг от друга будут катера через 3 ч? Через сколько времени они встретятся?
81. Из пункта А одновременно в противоположных направлениях выехали автомобиль и автобус. Через 3 ч после начала движения расстояние между ними составило 480 км. На каком расстоянии друг от друга они находились через 2 ч после начала движения? Какова скорость автобуса, если автомобиль ехал со скоростью 96 км/ч?
82. Придумай и реши задачи по схемам:
83. Что такое дробь? Что показывают числитель и знаменатель дроби 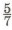 ? Что означает запись 18%? ? Что означает запись 18%?
84. Как найти: а) часть от числа, выраженную дробью; б) число по его части, выраженной дробью; в) часть, которую одно число составляет от другого?
85. "Блиц-турнир".
а) Кот Леопольд поймал а рыбок. 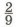 всех рыбок у него украла лиса. Сколько рыбок у него осталось? всех рыбок у него украла лиса. Сколько рыбок у него осталось?
б) В цирке выступало b слонов, что составило 12 % всех дрессированных животных этого цирка. Сколько в цирке дрессированных животных?
в) Иван-царевич n км скакал на коне, а m км летел на ковре-самолете. Какую часть пути скакал Иван-царевич на коне?
86. Длина одной стороны треугольника равна 36 см, что составляет 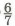 длины его второй стороны. Длина третьей стороны равна длины его второй стороны. Длина третьей стороны равна 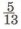 от суммы длин первых двух сторон. Найди периметр треугольника. от суммы длин первых двух сторон. Найди периметр треугольника.
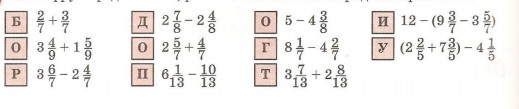
87. Расшифруй предложение, расположив ответы в порядке возрастания:
Петерсон Людмила Георгиевна. Математика. 4 класс. Часть 3. - М.: Издательство "Ювента", 2005, - 64 с.: ил.
Библиотека с учебниками и книгами на скачку бесплатно онлайн, Математика для 4 класса скачать, школьная программа по математике, планы конспектов уроков
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|