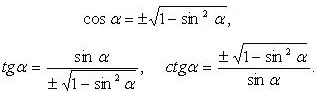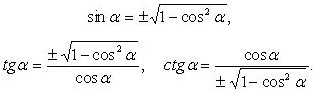|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Значения синуса, косинуса и тангенса некоторых углов. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
Вступительное словоТрадиционно в школе впервые знакомятся с синусом, косинусом и тангенсом острого угла в 8-м классе. Определения их вводятся через отношения в прямоугольном треугольнике. Такое представление трудно воспринимается и запоминается восьмиклассниками, – отсутствует опора на зрительное восприятие данных объектов. Мы решили пойти несколько иным путём: попытаться дать возможность «увидеть» синус и косинус, тангенс и котангенс угла.
Повторение ранее изученногоУгловая мераУгол измеряют в градусной мере (градус, минута, секунда), в оборотах — отношение длины дуги s к длине окружности L, в радианах — отношение длины дуги s к радиусу r; исторически применялась также градовая мера измерения углов, в настоящее время она почти нигде не используется. 1 оборот = 2 В системе СИ принято использовать радианы. В морской терминологии углы обозначаются румбами.
Углы на тригонометрической окружностиВ математике в качестве начала отсчёта углов принято направление оси абсцисс (то есть для наблюдателя, расположенного в начале координат, — относительно направления направо), и отсчитывается против часовой стрелки.
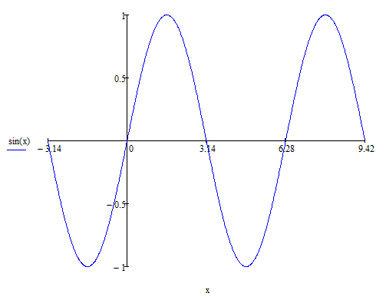
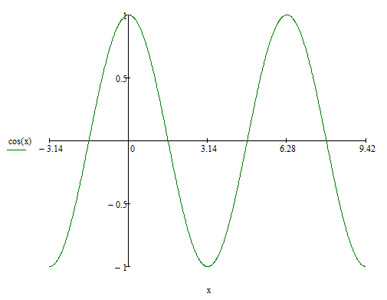
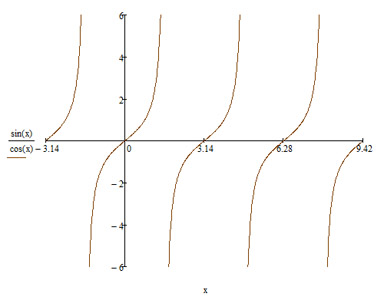
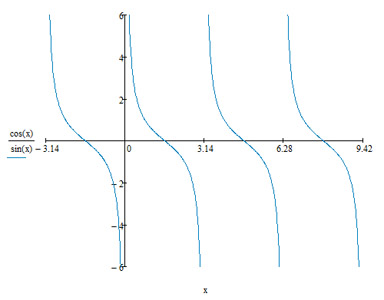
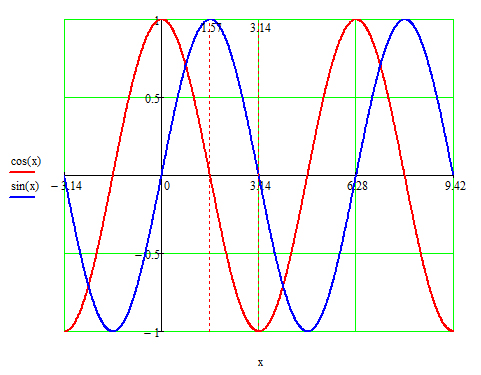
Определения синуса, косинуса и тангенсаДля того что бы мы могли разговаривать на "одном" языке - нужно посмотреть в сам корень и вспомнить что такое тригонометрия и тригонометрические функции. Тригонометрия - это такое сложное греческое слово: тригонон - треугольник, метро - мерять. Стало быть по-гречески это означает: меряться треугольниками. Очень странное слово. Может быть древнегреки под треугольниками подразумевали кое-что другое? Не знаю. Тригонометрические функции — вид элементарных функций, изучаемых в тригонометрии. Обычно к ним относят синус (sin x), косинус (cos x), тангенс (tg x), котангенс (ctg x), секанс (sec x) и косеканс (cosec x), последняя пара функций в настоящее время сравнительно малоупотребительна. В западной литературе тангенс, котангенс и косеканс обозначаются tan x, cot x, csc x. Обычно тригонометрические функции определяются геометрически, но можно определить их аналитически через суммы рядов или как решения некоторых дифференциальных уравнений, что позволяет расширить область определения этих функций на комплексные числа. Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
Синус (sin)Синус - тригонометрическая величина означающая половину хорды двойной дуги или угла а также перпендикуляр, опущенный из конца дуги на радиус. В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе. Значения синусов для часто встречающихся углов:
Косинус (cos)Косинус - синус дополнительного угла, функция угла, выражаемая отношением прилегающего к углу катета к гипотенузе. В прямоугольном треугольнике косинус острого угла равен отношению катета, выходящего из этого угла (прилежащего катета), к гипотенузе. Значения косинусов для часто встречающихся углов:
Тангенс (tg)Тангенс — одна из тригонометрических функций, обозначется tg (в англоязычной традиции — tan). В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему. Значение тангенса легко найти, зная синус и косинус угла: tg(α) = sin(α)/cos(α). Значения тангенсов для часто встречающихся углов:
Котангенс (ctg)Котангенс - одна из тригонометрических функций, обозначется ctg. Котангенсом угла в треугольнике называют отношение прилежащего катета, к противолежащему катету. сtg(α) = cos(α)/sin(α). Значения котангенсов для часто встречающихся углов:
Историческая справкаВ IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Дугу он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна). Слово косинус намного моложе. Косинус – это сокращение латинского выражения completely sinus, т. е. “дополнительный синус” (или иначе “синус дополнительной дуги”; cosa = sin( 90° - a)). Тангенсы возникли в связи с решением задачи об определении длины тени. Тангенс (а также котангенс) введен в X веке арабским математиком Абу-ль-Вафой, который составил и первые таблицы для нахождения тангенсов и котангенсов. Однако эти открытия долгое время оставались неизвестными европейским ученым, и тангенсы были заново открыты лишь в XIV веке немецким математиком, астрономом Регимонтаном (1467 г.). Он доказал теорему тангенсов. Региомонтан составил также подробные тригонометрические таблицы; благодаря его трудам плоская и сферическая тригонометрия стала самостоятельной дисциплиной и в Европе. Название «тангенс», происходящее от латинского tanger (касаться), появилось в 1583 г. Tangens переводится как «касающийся» (линия тангенсов – касательная к единичной окружности). Дальнейшее развитие тригонометрия получила в трудах выдающихся астрономов Николая Коперника (1473-1543) – творца гелиоцентрической системы мира, Тихо Браге (1546-1601) и Иогана Кеплера (1571-1630), а также в работах математика Франсуа Виета (1540-1603), который полностью решил задачу об определениях всех элементов плоского или сферического треугольника по трем данным.
Значения синуса, косинуса и тангенса некоторых угловПримерОдним из самых простых примеров применения синуса и косинуса является прямоугольный треугольник. Рассмотрим прямоугольный равнобедренный треугольник с углом при основании, равным 45°. Пусть катеты его равны a. Из за того что функция косинус опережает синус на 90 градусов возникло такое тождество. На графике видно то что разница между функциями равно 90 градусов. Выражение тригонометрических функций через одну из них того же аргумента.(выбор знака перед корнем зависит от того, в какой четверти находится угол а) Через sin(a):
Через cos(a):
Интересный фактТригонометрия в жизни. Итак, предположим, что нам необходимо построить мост между берегом реки и островом, а для этого нужно знать расстояние до объекта. Измерить это расстояние непосредственным образом трудно, поскольку на нашем пути река, крутые берега и лес. С точки зрения математики, перед нами стоит следующая задача: определить расстояние между точками А и В. Для решения этой задачи, мы будем использовать изученные определения из тригонометрии. Почему? Потому, что именно в тригонометрии изучаются взаимосвязи между сторонами прямоугольного треугольника и его углами. Но у нас нет пока прямоугольного треугольника, поэтому, мы будем его достраивать. Первое, что мы сделаем, это проведем прямую линию АМ так, чтобы образовался прямой угол МАВ. На этой прямой отмерим, например, 300 метров от точки А и поставим точку С. Теперь, мы имеем прямоугольный треугольник АВС. Далее, нам нужно измерить угол АСВ. В этом случае для измерения углов используется специальный прибор, позволяющий измерять углы между двумя объектами на местности. Предположим, используя этот прибор, мы получили угол АСВ равный 48 градусам. Итак, что мы имеем: мы имеем прямоугольный треугольник АВС; мы знаем расстояние АС, равное 300 метрам; знаем, что угол АСВ равен 48 градусам. Мы выполнили все подготовительные действия и теперь можем переходить непосредственно к вычислениям. Вспомним определение тангенса. Тангенс острого угла равен отношению противолежавшего катета к прилежащему. Из этого определения нам известны угол АСВ и сторона АС. Осталось определить сторону АВ. tg ACB = AB/AC или tg 48о = AB/AC Поскольку значения тангенсов для всех углов уже заранее подсчитаны, то мы просто берем готовое значение. Получаем: 1,1106 = АВ/300, отсюда: АВ = 1,1106 * 300 = 333 метра. Таким образом, мы получили расстояние АВ, зная взаимосвязь между острым углом прямоугольного треугольника и его сторонами. Вопросы
Список использованных источников
Потурнак С.А. Самылина Марина Валентиновна.
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: