|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Изменение синуса, косинуса и тангенса при возрастании угла. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
Повторение ранее изученного материалаНачнем с самого начала и вспомним то что будет полезно освежить в памяти. Что же такое синус, косинус и тангенс и к какому разделу геометрии относятся эти понятия. Тригонометрия - это такое сложное греческое слово: тригонон - треугольник, метро - мерять. Стало быть по-гречески это означает: мерятся треугольниками.
Основное применение тригонометрические функции получили в треугольниках, так как треугольник является простейшим многоугольником. Со всех геометрических фигур можно получить треугольник проведя не сложные построения этот процесс называется триангуляция. Вкратце говоря для того что бы решить сложную задачу ее легче разбить на несколько легких. Треугольник — простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны; часть плоскости, ограниченная тремя точками, и тремя отрезками, попарно соединяющими эти точки. Треугольники можно классифицировать по виду углов и по числу равных сторон. Типы треугольников: По виду углов: Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:
По числу равных сторон:
Также если мы уже заговорили про треугольники нужно вспомнить египетский треугольник. Египетский треугольник – прямоугольный треугольник с соотношением сторон 3:4:5. Сумма указанных чисел (3+4+5=12) с древних времен использовалась как единица кратности при построении прямых углов с помощью веревки, размеченной узлами на 3/12 и 7/12 ее длины. Применялся египетский треугольник в архитектуре средних веков для построения схем пропорциональности.
Задачи на повторениеЗадача №1Высота треугольника меньше 1. Может ли его площадь быть больше 10000 квадратных единиц? Ответ: Может. Таким будет, например, равнобедренный треугольник, основание которого равно 80000, а высота к основанию равна 0.5. Задача №2На рисунке изображено 2 треугольника. Верхний треугольник состоит 4-х фигур. Нижний треугольник (такой же площади) состоит из тех же фигур такой же площади. Вопрос — откуда взялся свободный квадратик? Ответ: Если присмотреться то будет видно что гипотенуза обеих треугольников немного (почти незаметно) деформирована. В первом она вогнута к основанию, а во втором наоборот. За счет этого и появляется свободный квадрат.
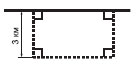
Задача №3Водителям приходится объезжать этот участок по запасному пути, отмеченному на плане пунктиром. На сколько километров увеличивает путь этот объезд? Ответ: 6 км. Для тех кто невнимательно прочитал условие задача покажется глупой и ответ не правильным, но самый подвох лежит как раз там. В условие сказано что НА сколько увечится путь, т.е. сколько лишних участков дороги водителям прийдеться проехать.
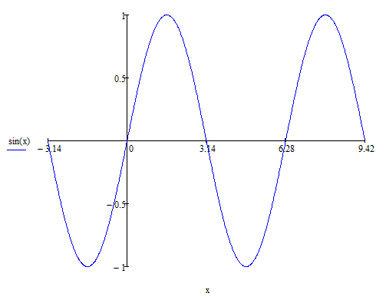
Изменение синуса, косинуса и тангенса при возрастании углаСинус (sin)Синус - тригонометрическая величина означающая половину хорды двойной дуги или угла а также перпендикуляр, опущенный из конца дуги на радиус. В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе. Как видно с графика, максимальное свое значение синус принимает в точке π/2. Расмотирим подробней. И так в точке 0 синус равен 0. На промежутке от 0 до 90 градусов синус принимает значения от 0 до 1 и в точке (π/2) достигает своего максимального значения. После чего тенденция прироста меняется и от 90 до 180 градусов синус начинает спадать и в точке πравняется обратно 0. На отрезке 180-270 синус продолжает уменьшатся и в точке 3π/2 принимает минимальное значение -1. И заканчивает свой цикл на промежутке 270-360 (3π/2-2π) принимает значения от -1 до 0. Эта закономерность продолжается до бесконечности. Сколько не продолжать график колебания будут оставаться такими же и не ожиданых отклонений не будет. Значения синусов для часто встречающихся углов:
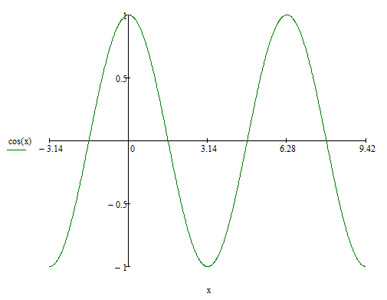
Косинус (cos)Косинус - синус дополнительного угла, функция угла, выражаемая отношением прилегающего к углу катета к гипотенузе. В прямоугольном треугольнике косинус острого угла равен отношению катета, выходящего из этого угла (прилежащего катета), к гипотенузе. Косинус это дополнительная функции синуса. И имеет тот же характер что и синус только есть некоторые нюансы и отличия. Как видно с графиков синуса и косинуса они отличается ровна на 90 градусов (π/2).Как Вы уже и сами заметили синус начинается с 0, а косинус с 1.Что ведет за собой зависимость - на промежутку от 0 до 90 градусов косинус уменьшается и в точке π/2 принимает значения равное 0. После чего он уменьшается дальше и на промежутку от π/2 до πпринимает значения от 0 до -1. И только по достижению угла равного 180 градусов косинус достигает своего минимального значения и равняется -1. На промежутку 180-270 градусов косинус принимает значения от -1 до 0. И вот 270-360 градусов косинус стремится от 0 до единицы. Таким образом функция косинуса проходит свой полный цикл и повторяет его заново. Такая последовательность продолжается до бесконечности. Значения косинусов для часто встречающихся углов:
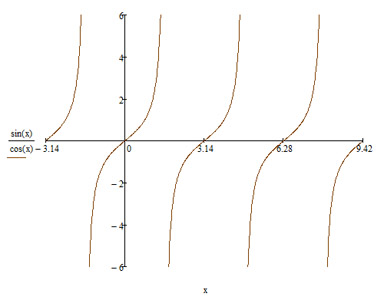
Тангенс (tg)Тангенс — одна из тригонометрических функций, обозначется tg (в англоязычной традиции — tan). В прямоугольном треугольнике тангенс острого угла равен отношению противолежащего катета к прилежащему. Значение тангенса легко найти, зная синус и косинус угла: tg(α) = sin(α)/cos(α). С тангенсом уже немого сложнее потому что его значение зависит уже от двух функций. Как видно выше, тангенс равен соотношению синуса и косинуса. В некоторых точках тангенс не определен, это обусловлено тем что косинус в точках π/2 и 3π/2 равен нулю в следствии чего получается деление на ноль. Теперь про сами изменения на промежутках. Первый это от 0 до 90 градусов, в точке 0 тангенс равен 0, а в точке π/2 не определен но знак + в некоторых книгах говорят что в этой точке значение равно +∞ что тоже является верным. Второй промежуток 90-180 (π/2-π) можно сказать что здесь функция возвращается обратно в ноль и принимает значения от +∞ до 0. Третий промежуток: 180-270 значение от 0 до -∞. И последний участок это 270-360 градусов, где значение функции изменяется от -∞ до 0. Значения тангенсов для часто встречающихся углов:
Практическое применениеНа практике синус, косинус применяются в многих расчетах какие люди просто не замечают или просто не сталкиваются с ними. Самый простой пример это задача по физике, про дальность полета брошеного предмета под углом. Рассмотрим эту задачу: Хорошо известно, что максимальная дальность полета тела, брошенного под углом к горизонту, достигается при угле вылета равном 45° и определяется формулой: В основном область применений тригонометрических функций это расчеты какие нельзя получить экспериментально или какие нужно подтвердить теоретически.
Интересный факт
Альфред Нобель (1833–1896)
Число Пи
Вопросы
Список использованных источников
Потурнак С.А. Самылина Марина Валентиновна
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: