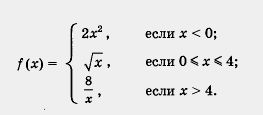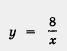|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Исследование функций на монотонность
Исследование функций на монотонность
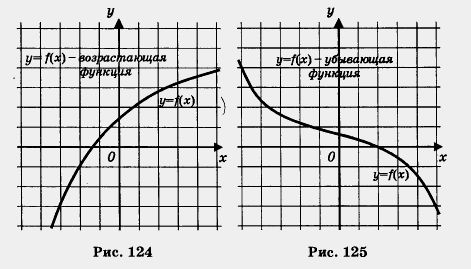
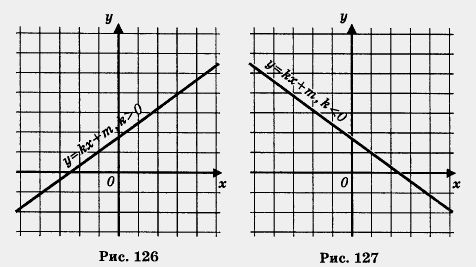
Определение 1.Функцию у = f(x) называют возрастающей на промежутке X, если из неравенства х1 < х2- где хг и х2 — любые две точки промежутка X, следует неравенство f(x1) < f(x2). Определение 2. Функцию у = f(x) называют убывающей на промежутке X, если из неравенства х1 < х2, где х1 и х2 — любые две точки промежутка X, следует неравенство f(x1) > f(x2). На практике удобнее пользоваться следующими формулировками: функция возрастает, если большему значению аргумента соответствует большее значение функции; Используя эти определения и установленные в § 33 свойства числовых неравенств, мы сможем обосновать выводы о возрастании или убывании ранее изученных функций.
1. Линейная функция у = kx +m Если k > 0, то функция возрастает на всей числовой прямой (рис. 126); если k < 0, то функция убывает на всей числовой прямой (рис. 127). Доказательство. Положим f(х) = kx +m. Если х1 < х2 и k > О, то, согласно свойству 3 числовых неравенств (см. § 33), kx1 < kx2. Далее, согласно свойству 2, из kx1 < kx2 следует, что kx1 + m < kx2 + m, т. е. f(х1) < f(х2).
Если же х1 < х2 и k < 0, то, согласно свойству 3 числовых неравенств, kx1 > kx2, а согласно свойству 2, из kx1 > kx2 следует, что kx1 + m> kx2 + т. Итак, из неравенства х1 < х2 следует, что f(х1) > f(х2). Это и означает убывание функции у = f(x), т. е. линейной функции у = kx + m. Если функция возрастает (убывает) во всей своей области определения, то ее можно называть возрастающей (убывающей), не указывая промежутка. Например, про функцию у = 2х - 3 можно сказать, что она возрастает на всей числовой прямой, но можно сказать и короче: у = 2х - 3 — возрастающая
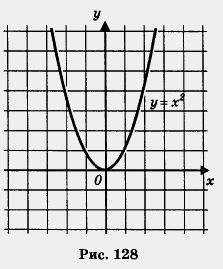
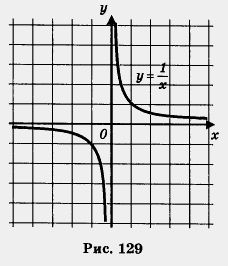
1. Рассмотрим функцию у = х2 на луче [0, + 00). Пусть 0 2. Рассмотрим функцию у = х2 на луче (- со, 0]. Возьмем два неположительных числа х1 и х2, таких, что х1 < х2. Тогда, согласно свойству 3 числовых неравенств, выполняется неравенство - х1 > - х2. Так как числа - х1 и - х2 неотрицательны, то, возведя в квадрат обе части последнего неравенства, получим неравенство того же смысла (-х1)2 > (-х2)2, т.е. Итак, из неравенства х1 < х2 следует, что f(х1) > f(х2). Поэтому функция у = х2 убывает на луче (- 00, 0] (рис. 128). Итак, из неравенства х1 < х2 следует, что f(x1) > f(x2). Это значит, что функция убывает на открытом луче (0, + 00) (рис. 129).
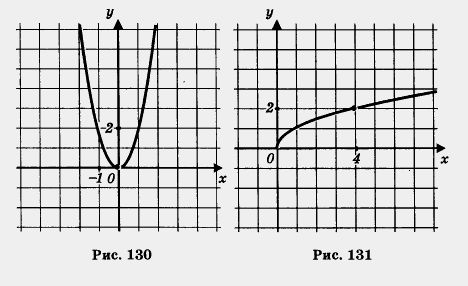
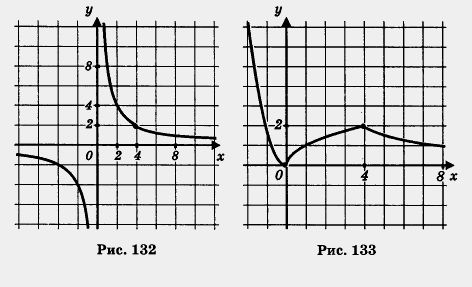
Итак, из неравенства х1 < х2 следует, что f(x1) >f(x2) т.е. функция убывает на открытом луче (-00, 0) Обычно термины «возрастающая функция», «убывающая функция» объединяют общим названием монотонная функция, а исследование функции на возрастание и убывание называют исследованием функции на монотонность. Пример. Построить и прочитать график функции y = f{x), где 1) Построим график функции у = 2х2 и возьмем ветвь этой параболы при х < 0 (рис. 130). 2) Построим график функции
Прочитаем график функции у = f(x). 1. Область определения функции — вся числовая прямая. 2. у = 0 при х = 0; у > 0 при х > 0. 3. Функция убывает на луче (-оо, 0], возрастает на отрезке [0, 4], убывает на луче [4, + оо). 4. Функция ограничена снизу, но не ограничена сверху. 5. унаим. = 0 (достигается при х = 0); Yнаиб- не существует. 6. Функция непрерывна. 7. Область значений функции — луч [0, + оо). 8. Функция выпукла вниз на луче (-оо, 0], выпукла вверх на отрезке [0, 4], выпукла вниз на луче [4, + оо).
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: