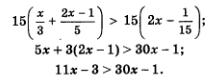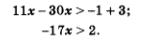|
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика:Линейные и квадратные неравенства
Линейные и квадратные неравенства Прочитав название параграфа, вы, наверное, спросите: «Почему мы топчемся на месте?». В самом деле, линейные и квадратные неравенства с одной переменной вы научились решать в курсе алгебры 8-го класса — это была одна из последних тем курса. Почти ничего нового вы из этого параграфа не узнаете, более того, обнаружите, что некоторые примеры заимствованы из учебника «Алгебра-8». Рассматривайте этот параграф как возможность повторения, которое позволит вам плавно перейти к изучению новой темы (в следующем параграфе). Два неравенства Обычно при решении неравенства стараются заменить данное неравенство более простым, но равносильным ему. Такую замену называют равносильным преобразованием неравенства. Эти преобразования указаны в сформулированных ниже правилах 1—3. Правило 1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком (не меняя при этом знака неравенства). Например, неравенство Зх + 5 < х2 равносильно неравенству -х2 + Зх + 5 < О (член х2 перенесли из правой части неравенства в левую с противоположным знаком). Правило 2. Обе части неравенства можно умножить или разделить на одно и то же положительное число,не меняя при этом знака неравенства. Например, неравенство 8х - 4 > 12х2 равносильно неравенству 2х - 1 > Зх2 (обе части первого неравенства разделили на положительное число 4). Правило 3. Обе части неравенства можно умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный Правила 2 и 3 допускают следующие обобщения (соответствующие утверждения представляют собой теоремы, но мы, ради удобства читателя, оформим их в виде правил): Правило 2*. Если обе части неравенства с переменной х умножить или разделить на одно и то же выражение р(х), положительное при всех значениях х, и сохранить знак исходного неравенства, то получится неравенство, равносильное данному. Правило 3*. Если обе части неравенства с переменной х умножить или разделить на одно и то же выражение р(х), отрицательное при всех значениях х, и изменить знак исходного неравенства на противоположный, то получится неравенство, равносильное данному. Например, неравенство (2х + 1)(х2 + 2) > 0 равносильно неравенству 2х + 1 > 0 (обе части исходного неравенства разделили на выражение х2 + 2, положительное при любых значениях х; при этом знак исходного неравенства оставили без изменения). Решение. Умножим обе части неравенства на положительное число 15, оставив знак неравенства без изменения (второе правило). Это позволит нам освободиться от знаменателей, т.е. перейти к более простому неравенству, равносильному данному:
Наконец, применив третье правило, получим
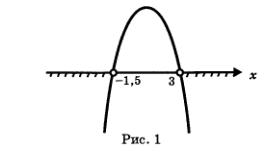
Решение. 1) Преобразуем неравенство к виду Зх + 9 -- 2х2 < О (выполнили равносильное преобразование неравенства). Найдем корни квадратного трехчлена -2х2 + Зх + 9; для этого решим квадратное уравнение -2х2 + Зх + 9 = 0:
От в ет: х <-1,5; х > 3. Полезно вспомнить два утверждения, которые были доказаны в курсе алгебры 8-го класса и не раз понадобятся нам в дальнейшем. 1. Если квадратный трехчлен ах2 + Ьх + с не имеет корней (т.е. его дискриминант D — отрицательное число) и если при этом а> О, то при всех значениях х выполняется неравенство ах2 + Ьх + с> 0. Иными словами, если D> < 0, а > 0, то неравенство ах2 + bх + с > О выполняется при всех х; напротив, неравенство ах2 + bх + с < 0 в этом случае не имеет решений. 2. Если квадратный трехчлен ах2 + Ьх + с не имеет корней (т.е. его дискриминант D> — отрицательное число) и если при этом а< О, то при всех значениях х выполняется неравенство ах2 + Ьх + с< 0. Иными словами, если 1> < 0, а < 0, то неравенство ах2 + Ьх + с <0 выполняется при всех х; напротив, неравенство ах2 + Ьх + с > О в этом случае не имеет решений. Эти утверждения суть частные случаи следующей теоремы.
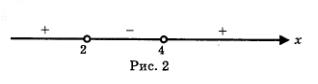
Р е ш е н и е. а) Найдем дискриминант квадратного трехчлена 2x2 -х + 4. Имеем б) Найдем дискриминант квадратного трехчлена -х2 + Зх - 8. Имеем О т в е т: а) (-оо,+оо); б) нет решений. В следующем примере мы напомним вам еще один способ рассуждений, который можно применять при решении неравенств. Пример 4. Решить неравенство х2 - 6х + 8 > 0. Решение. Разложим квадратный трехчлен х2 - 6х + 8 на множители. Корнями трехчлена являются числа 2 и 4. Воспользовавшись формулой ах2 + Ьх + с = а(х - хb)(х - х2), получим х2 - 6х + 8 = (х - 2)(х - 4). Отметим на числовой прямой корни трехчлена: 2 и 4 (рис. 2). Выясним, когда произведение (х - 2) (х - 4) положительно, а когда — отрицательно. Если х>4,то х-2>0 и х-4>0,значит,(х-2)(х-4)>0. Если 2<х<4, тох-2>0, ах-4<0, значит, (х - 2) (х - 4) < 0. Если, наконец, х<2,тоих-2<0, их~4<0, а потому (х - 2) (х - 4) > О (рис. 2). Спрашивается, при каких значениях переменной х квадратный трехчлен х2 - 6х + 8 принимает положительные значения? С помощью геометрической модели, представленной на рис. 2, делаем вывод: указанный квадратный трехчлен принимает положительные значения на двух открытых лучах — (-оо, 2) и (4, +оо). От в ет: х < 2; х > 4. Метод рассуждений, который мы применили в примере 4, называют обычно методом интервалов (или методом промежутков). Он активно используется в математике для решения рациональных неравенств. В следующем параграфе мы изучим метод интервалов более детально, а этот параграф, чтобы не ограничиваться в нем только напоминанием известного, завершим примером, в котором речь идет о решении так называемых «неравенств с модулями». Пример 5. Решить неравенство: Например,
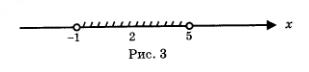
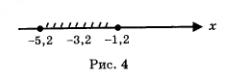
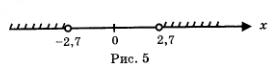
О т в е т: а) -1 < x < 5; б) -5,2 <x < -1,2; в) x < -2,7;x > 2,7.
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: