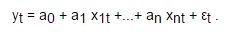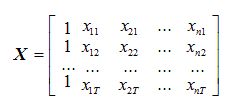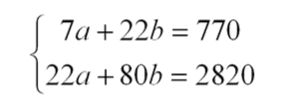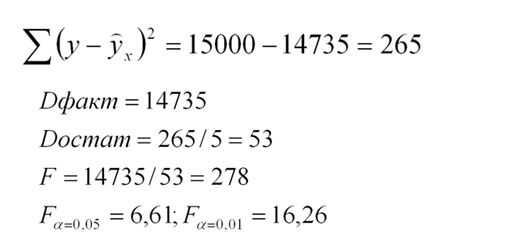|
Гипермаркет знаний>>Информатика>>Информатика 11 класс>>Информатика: Метод наименьших квадратов
Метод наименьших квадратов Что такое метод наименьших квадратов?Сегодняшний наш урок будет посвящен изучению темы о методах наименьших квадратов. Что же это за метод? Давайте начнем с его определения. Методом наименьших квадратов называют такой метод, при котором нахождение оптимальных параметров линейной регрессии, имеет в сумме квадратов регрессионных остатков минимальное количество ошибок. В этом методе ключевым моментом выступает, минимизация евклидова расстояния
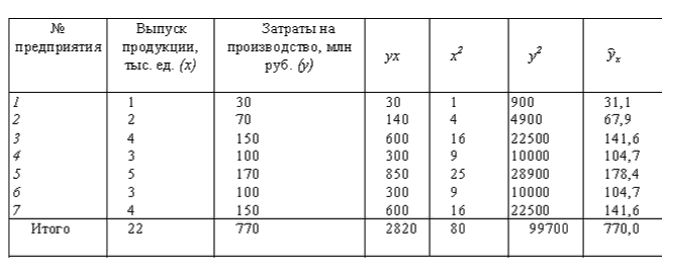
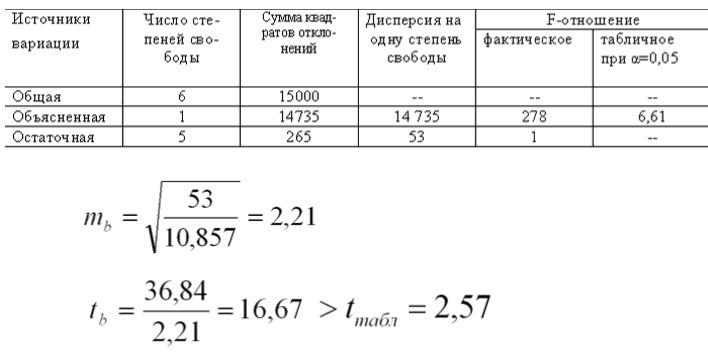
между вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной. Для линейных экономических моделей метод наименьших квадратов является не только самым распространенным, но и наиболее простым и эффективным методом оценки данных параметров Уt. Но даже при том, что этот метод принято считать наиболее эффективным, все же при его применении следует быть осторожными, так как построенные по методу наименьших квадратов модели, не всегда соответствуют требованиям к качеству их параметров и поэтому не всегда способны с точностью отображать все закономерности, участвующие в развитии процесса. Ну а сейчас давайте более подробно попробуем рассмотреть процесс оценки параметров линейной эконометрической модели, используя метод наименьших квадратов. В общем виде эта модель может иметь уравнение такого вида, как: При оценке таких параметров, как a0 , a1 ,..., an, его исходными данными будет вектор, у которого значения зависимой переменной y = (y1 , y2 , ... , yT )', а также матрица значений независимых переменных: если рассматривать первый столбец, то он состоит из единиц, которые соответствуют коэффициенту этой модели. Метод наименьших квадратов свое название приобрел, благодаря принципу, которому должны удовлетворять оценки параметров, полученные на его основе. Притом, что касается оценки его параметров, то сумма квадратов ошибки данной модели должна быть минимальной. Теперь давайте более наглядно метод наименьших квадратов рассмотрим на примере: В таблице наведен перечень предприятий, которые выпускают один и тот же товар. Давайте рассмотрим функции издержек: В этом случае мы с вами видим, что система нормальных уравнений предоставлена в таком виде: Из этого следует, что: а = - 5,79; b = 36,84. Получаем уравнение регрессии: В итоге мы видим, что общая сумма квадратов будет равна: Из этого следует, что факторная сумма квадратов приобретает такой вид: Ну и остаточная сумма квадратов выходит: Приходим к такому выводу, что уравнение регрессии значимо и F факт больше F табл. Дисперсионный анализ результатов регрессииИспользование методов наименьших квадратовВозникает вполне закономерный вопрос, зачем нам нужен и где может быть использован метод наименьших квадратов? Ну, естественно, что в первую очередь МНК нашел свое применение в математике. А именно: • Во-первых, он необходим в как, так и в теории вероятности, так и в математической статистике; |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: