|
Гіпермаркет Знань>>Математика>>Математика 6 клас>>Модуль числа
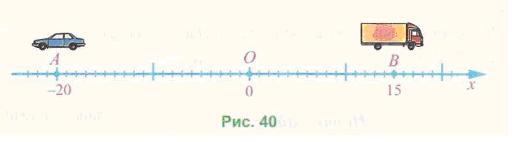
Нехай з пункту О у протилежних напрямах виїхали два автомобілі й через деякий час перший був у точці А(-20), а другий — у точці #(15) (рис. 40).
Який з автомобілів проїхав більшу відстань?
Щоб відповісти на це запитання, потрібно порівняти відстані ОА й ОВ. Оскільки ОА = 20, ОВ = 15 і 20 > 15, то більшу відстань проїхав перший автомобіль.
Отже, щоб відповісти на запитання, ми порівнювали не числа -20 і 15, а числа «без знаків» 20 і 15, або ще кажуть: порівнювали модулі чисел -20 і 15.
Модулем додатного числа і нуля називають саме число. Модулем від'ємного числа називають протилежне йому додатне число.
Для позначення модуля числа використовують дві вертикальні риски, тобто пишуть |15| = 15 (читають: модуль п'ятнадцяти дорівнює п'ятнадцять).
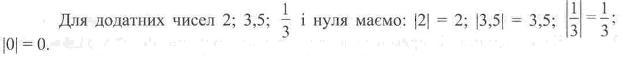
Модулем від'ємного числа називають протилежне йому додатне число.
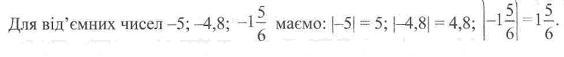
Отже, модулем будь-якого числа є додатне число або число 0. З геометричної точки зору модуль числа дорівнює відстані на координатній прямій від початку відліку до точки, яка зображує це число (рис. 41).
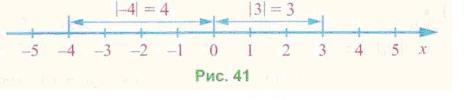
Модуль числа 3 дорівнює 3, і відстань від початку відліку до точки, що відповідає цьому числу, дорівнює 3. Модуль числа -4 дорівнює 4, і відстань від початку відліку до точки, що відповідає цьому числу, дорівнює 4.
Якщо |х| = 3, то х = 3 або х = -3;
якщо |х| = 0, то х = 0;
не існує числа, для якого виконувалася б рівність |х| = -3, оскільки модуль будь-якого числа є завжди додатним числом або нулем.
Протилежні числа мають рівні модулі. Наприклад, для протилежних чисел -2 і 2 |-2| = 2і|2| = 2.
Прочитайте
1. Розв'язати рівняння: 3|х| + 4,5 = 9,3.
• 3|.т| = 9,3 - 4,5; 3|х| = 4,8; |.т| = 4,8:3; |х| = 1,6; х = 1,6 або х =-1,6. •
2. Знайти від'ємні цілі числа, для яких \х\ < 3.
• Такими числами є:
х = -1,бо |-1| = 1 і 1<3;
х = -2, бо |-2| = 2 і 2 < 3 1
Модулі решти від'ємних цілих чисел (-3; -4; -5; -6; -7; ...) більші від З або дорівнюють 3.
3. На координатній прямій позначити точки, координати яких задовольняють умову |х| < 2,6. Знайти від'ємні цілі числа, які задовольняють цю умову.
Умову |х| < 2,6 задовольняють числа, які на координатній прямій лежать між числами -2,6 і 2,6. Ця частина координатної прямої на рисунку 42 заштрихована.

Від'ємними цілими числами, які задовольняють умову |х| < 2,6, є лише числа-2 і-1. •
Усно
943. Чому дорівнює модуль кожного із чисел: 1,2; -7; 0; -0,3; -1,2; 4,1; 0,15? Чи може число мати від'ємний модуль?
944. Яка відстань від початку відліку до кожної з точок: А(3); В(-5); С(—1,3); £>(0,8)?
945. Відомо, що \а\ = 10. Чому дорівнює а?
Рівень А
946. Знайдіть модуль кожного із чисел: 2,1; -1,8; 0,2; -3,01; -0,23. Запишіть відповідні рівності.
947. Знайдіть |х|, якщо х = -5,6; х = 100; х = -0,01; х = 0,27; х = -40,2.
948. Знайдіть х, якщо:
а)|х| = 6; б)|х|=±; в)|х| = 1,2; г) |х| = 0; д)|х|=-2.
949. Запишіть усі числа, що мають модуль 15; 0; 0,7.
950. Позначте на координатній прямій числа, модулі яких дорівнюють: 950. 2;3;0;4,5;0,5.
951. 1; 2,5; 3,5; 4.
952. Знайдіть:
а) додатне число, модуль якого дорівнює: 14; 19,5; 0,29; 7,2; -1;
б) від'ємне число, модуль якого дорівнює: 2; 5,1; 89; 20; -5.
Запишіть відповідні рівності.
Знайдіть значення виразу:
953. а) |-517| - |3111; б) |-10| • |-2,5|; в) |-6,4| : 1,6;
г)|-7,2|:|-1,8|; д) |-0,5| • |-0,1|; е) 1,51 + |-0,372|.
954.
а) |-1,7| - |-0,9|; б) 110,2| + |-3,8|; в) |-65| • 0,8;
г) 1-4,21 : 1-141; д) 1-2,51 • 1-201; е) |-1,05| : |1,5|.
955. Порівняйте модулі чисел:
а) 3,81 і -3,01; б) —11,1 і —12; в) 0,72 і-0,73;
г) 5,1 і 0; д) 19,1 і 49,1; е) -12,3 і 0.
Виберіть число, модуль якого найбільший:
а) 14,2; -15; 2; -18; 13,5; б) -90; 53,4; -7; -63,8.
Рівень Б

Знайдіть усі цілі числа, для яких виконується умова:
Знайдіть усі цілі числа, для яких виконується умова:
961. а) |х| < 4; б) 1*1 < - ; в) |х| < 2,53; г) |х| <-2.
962. а)|х|<2; б) ]х| < 1; в)|х|<3,8; г)|х|<0.

965. Знайдіть усі від'ємні цілі числа, для яких виконується умова |х| < 7.
На координатній прямій позначте точки, координати яких задовольняють умову:
966. а)|х|<3; б) 1*1 < 2-.
967.
а)|х|<2; б)|х|<3,5.
968. а) Знайдіть відстань між точками М(х) і Щ-х), якщо х = -2,5.
б) Знайдіть |х|, якщо відстань між точками М(х) і Л^-х) дорівнює 6 одиниць.
969. Відомо, що а = -Ь. Чи правильно, що \а\ = \Ь\?
970. Відомо, що |х'| = |у|. Чи правильно, що х =у?
Здогадайтеся
971. Батько, що мав трьох синів, заповів, щоб після його смерті сини поділили табун коней так: старший син узяв половину всіх коней, середній — третину, а молодший — дев'яту частину усіх коней. Батько помер і залишив 17 коней. Сини не могли розділити коней і звернулися до мудреця. Він приїхав на своєму коні й розділив коней між синами так, що усі вони залишилися задоволеними. Як він це зробив?
Вправи для повторення
973. Розв'яжіть рівняння Зх - 3,5 = 8.
974. Знайдіть:
а) а, якщо -а = 2,6; -а = --; '-а - 0; б) -к; ~(-к), якщо к = 7.
975. Легковий і вантажний автомобілі рухаються назустріч один одному. Швидкість легкового автомобіля дорівнює 80 км/год, а швидкість вантажного становить 65% від швидкості легкового. Знайдіть відстань між автомобілями через 0,5 год після їх зустрічі.
976 . Із двох селищ, відстань між якими дорівнює 28 км, одночасно назустріч один одному виїхали два мотоциклісти. Швидкість одного мотоцикліста дорівнює 24 км/год, що становить 75% від швидкості іншого. Знайдіть відстань між мотоциклістами через 36 хв після їх виїзду із селищ.
Математика 6 клас Галина Янченко, Василь Кравчук
Вислано читачами iнтернет-сайту
Онлайн-бібліотека з підручниками і книгами, тести з математики, завдання з математики 6 клас, календарне планування
Зміст уроку
 конспект уроку і опорний каркас конспект уроку і опорний каркас
 презентація уроку презентація уроку
 акселеративні методи та інтерактивні технології акселеративні методи та інтерактивні технології
 закриті вправи (тільки для використання вчителями) закриті вправи (тільки для використання вчителями)
 оцінювання
Практика оцінювання
Практика
 задачі та вправи,самоперевірка задачі та вправи,самоперевірка
 практикуми, лабораторні, кейси практикуми, лабораторні, кейси
 рівень складності задач: звичайний, високий, олімпійський рівень складності задач: звичайний, високий, олімпійський
 домашнє завдання
Ілюстрації домашнє завдання
Ілюстрації
 ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа ілюстрації: відеокліпи, аудіо, фотографії, графіки, таблиці, комікси, мультимедіа
 реферати реферати
 фішки для допитливих фішки для допитливих
 шпаргалки шпаргалки
 гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення гумор, притчі, приколи, приказки, кросворди, цитати
Доповнення
 зовнішнє незалежне тестування (ЗНТ) зовнішнє незалежне тестування (ЗНТ)
 підручники основні і допоміжні підручники основні і допоміжні
 тематичні свята, девізи тематичні свята, девізи
 статті статті
 національні особливості національні особливості
 словник термінів словник термінів
 інше
Тільки для вчителів інше
Тільки для вчителів
 ідеальні уроки ідеальні уроки
 календарний план на рік календарний план на рік
 методичні рекомендації методичні рекомендації
 програми програми
 обговорення обговорення
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|