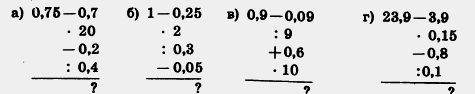|
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Наименьшее общее кратное
7. Наименьшее общее кратное
Решение. Число сантиметров пути должно делиться без остатка и на 75, и на 60, т. е. оно должно быть кратным и 75, и 60. Выпишем числа, кратные 75. Получим:75, 150, 225, 300, 375, 450, 525, 600, 675, 750, .... Затем выпишем числа, кратные 60. Получим: 60, 120, 180, 240, 300, 360, 420, 480, 540, 600, 660, .... Общими кратными чисел 75 и 60 будут числа 300, 600,.... Наименьшим из них является 300. Это число называют наименьшим общим кратным чисел 75 и 60. Значит, наименьшим расстоянием, на котором Володя и Катя сделают целое число шагов, будет 300 см. При этом Володя сделает 4 шага (300:75 = 4), а Катя — 5 шагов (300:60=5). Наименьшим общим кратным натуральных чисел а и b называют наименьшее натуральное число, которое кратно и а,и b. Наименьшее общее кратное чисел 75 и 60 можно найти и не выписывая подряд кратные этих чисел. Для этого разложим 75 и 60 на простые множители: 75=3 • 5 • 5, а 60=2 • 2 • 3 • 5. Выпишем множители, входящие в разложение первого из этих чисел, и добавим к ним недостающие множители 2 и 2 из разложения второго числа. Получаем пять множителей 2 • 2 • 3 • 5>5, произведение которых равно 300. Это число является наименьшим общим кратным чисел 75 и 60. Так же находят наименьшее общее кратное для трех и более чисел. Чтобы найти наименьшее общее кратное нескольких натуральных чисел, надо: 1) разложить их на простые множители; 2) выписать множители, входящие в разложение одного из чисел; 3) добавить к ним недостающие множители из разложений остальных чисел; 4) найти произведение получившихся множителей. Заметим, что если одно из данных чисел делится на все остальные числа, то это число и является наименьшим общим кратным данных чисел. Например, наименьшим общим кратным чисел 12, 15, 20 и 60 будет число 60, так как оно делится на все данные числа. ? Какое число называют наименьшим общим кратным натуральных чисел а и b? Как найти наименьшее общее кратное нескольких чисел? Какое число является наименьшим общим кратным чисел m и n, если число m кратно числу n? К 171. Найдите разложение на простые множители наименьшего общего кратного чисел а и 6, если: а) а=3 • 5, b = 7 • 5; б) а = 2 • 2 • 3 • 3 • 5, b = 2 • 2 • 3 • 7. 172. Найдите наименьшее общее кратное чисел а и b, если: а) а=2 • 2 • 3 • 5 • 5 и b = 2 • 3 • 3 • 3 • 5; 173. Найдите наименьшее общее кратное чисел: а) 6 и 8; в) 72 и 99; д) 34, 51 и 68; 176. Найдите наименьшее общее кратное чисел: а) 45 и 135; б) 34 и 170. Равно ли оно одному из данных чисел? 176. Вдоль дороги от пункта А поставлены столбы через каждые 45 м. Эти Столбы решили заменить другими, поставив их на расстоянии 60 м друг от друга. Найдите расстояние от пункта А до ближайшего столба, который будет стоять на месте старого. 177. В портовом городе начинаются три туристских теплоходных рейса, первый из которых длится 15 суток, второй 20 суток и третий 12 суток. Вернувшись в порт, теплоходы в этот же день снова отправляются в рейс. Сегодня из порта вышли теплоходы по всем трем маршрутам. Через сколько суток они впервые снова вместе уйдут в плавание? П 178. Вычислите устно:
180. Найдите наибольший общий делитель для числителя и знаменателя дроби: 181. Какие из следующих утверждений верны: а) два четных числа не могут быть взаимно простыми; б) четное и нечетное числа всегда взаимно простые; в) два различных простых числа всегда взаимно простые; г) простое и составное числа могут быть взаимно простыми; д) любое натуральное число и натуральное число, не являющееся ни простым, ни составным, обязательно взаимно простые; е) последовательные натуральные числа всегда взаимно простые. 182. Найдите наибольший общий делитель чисел: а) 12 и 24; б) 6 и 9; в) 75 и 45; г) 81 и 243; д) 4725 и 7875. 183. Лист картона имеет форму прямоугольника, длина которого 48 см, а ширина 40 см. Этот лист надо разрезать без отходов на равные квадраты. Какие наибольшие квадраты можно получить из этого листа? 184 Число т кратно 12. Докажите, что число m делится на 4. 185. Назовите все двузначные числа, записанные одинаковыми цифрами. Найдите наибольший общий делитель всех этих чисел. 186. Запишите в виде дроби частные: 3:7; 5:11: 23:34. 187. Запишите в виде частного дроби: 188. Запишите в виде обыкновенной дроби частные 18:7; 23:8; 16:5; 343:14 и выделите целые части. 189. Найдите среднее арифметическое чисел: 3,8; 4,2; 3,5; 4,1. 190. Среднее арифметическое двух чисел равно 54. Одно число в 2 раза больше другого. Найдите эти числа. 191. Решите задачу: 1) В цистерне было 38 т керосина. В первый день израсходовали в 2,4 раза больше керосина, чем во второй день. После этого в цистерне осталось 9,1 т керосина. Сколько тонн керосина израсходовано в первый день? 2) Утром на базе было 19 т муки. До обеда с базы выдали в 3,2 раза больше муки, чем после обеда. К вечеру на базе осталось 4,3 т муки. Сколько тонн муки выдали с базы до обеда? М 192. По таблице простых чисел (см. форзац) подсчитайте, сколько простых чисел в каждой из первых десяти сотен (т. е. среди чисел от 1 до 100, от 101 до 200 и т. д.). Заметили ли вы какие-либо закономерности в расположении простых чисел? Два простых числа, разность которых равна 2, называют близнецами. Найдите в таблице все пары чисел-близнецов. Какие из них самые большие? Сколько таких пар среди первых 500 натуральных чисел? среди чисел от 500 до 1000? Ученые до сих пор не знают, есть ли самая большая пара чисел- близнецов. Д 193. Найдите наименьшее общее кратное чисел: а) 18 и 45; б) 30 и 40; в) 210 и 350; г) 20, 70 и 15. 194 Найдите наименьшее общее кратное чисел а и b, если: а) а=5 • 5 • 7 • 13, b = 5 • 7 • 7 • 13; б) а = 504, b = 540. 195. Саша, Коля и Сережа собрали 51 стакан малины. Сережа собрал в 2 раза больше малины, чем Саша, а Коля — на 3 стакана больше, чем Саша. Сколько стаканов малины собрал каждый из мальчиков? 196. Масса первых трех искусственных спутников Земли, запущенных в 1957—1958 гг., была равна 1918,9 кг. Найдите массу каждого из этих спутников, если масса второго была больше массы первого на 424,7 кг, а масса третьего — больше массы второго на 818,7 кг. 197. Решите уравнение: а) (x+ 36,1) • 5,1 = 245,82; в) (x+ 24,3): 18,3 = 3,1; 198. Запишите в виде дроби частные 27:8; 72:8; 483:18; 1225:12 и выделите из них целые части. 199. Найдите среднее арифметическое чисел 5,24; 6,97; 8,56; 7,32 и 6,23. 200. Поезд шел 3 ч со скоростью 65,2 км/ч и 2 ч со скоростью 83,3 км/ч. Найдите среднюю скорость поезда за эти 5 часов. 201. Найдите значение выражения: а) 51 — (3,75:3 + 86,45:24,7) • 2,4; б) (650000:3125-196,5) • 3,14. A П и ф а г о р (VI в. до и. э.) и его ученики изучали вопрос о делимости чисел. Число, равное сумме всех его делителей (без самого числа), они называли совершенным числом. Например, числа 6 (6 = 1 + 2 + 3), 28 (28 = 1 + 2 + 4 + 7 + 14) совершенные. Следующие совершенные числа 496, 8128, 33 550 336. Пифагорейцы знали только первые три совершенных числа. Четвертое — 8128 — стало известно в I в. и. э. Пятое — 33 550 336 — было найдено в XV в. К 1983 г. было известно уже 27 совершенных чисел. Но до сих пор ученые не знают, есть ли - нечетные совершенные числа, есть ли самое большое совершенное число. Интерес древних математиков к простым числам связан с тем, что любое число либо простое, либо может быть представлено в виде произведения простых чисел, т. е. простые числа — это как бы кирпичики, из которых строятся остальные натуральные числа. Вы, наверное, обратили внимание, что простые числа в ряду натуральных чисел встречаются неравномерно — в одних частях ряда их больше, в других — меньше. Но чем дальше мы продвигаемся по числовому ряду, тем реже встречаются простые числа. Возникает вопрос: существует ли последнее самое большое простое число? Древнегреческий математик Евклид (III в. до н. а.) В своей книге «Начала», бывшей на протяжении двух тысяч лет основным учебником математики, доказал, что простых чисел бесконечно много, т. е. за каждым простым числом есть еще большее простое число. Для отыскания простых чисел другой греческий математик того же времени — Эратосфён придумал такой способ. Он записывал все числа от 1 до какого-то числа, а потом вычеркивал единицу, которая не является ни простым, ни составным числом, затем вычеркивал через одно все числа, идущие после 2 (числа, кратные 2, т. е. 4, 6, 8 и т. д.). Первым оставшимся числом после 2 было 3. Далее вычеркивались через два все числа, идущие после 3 (числа, кратные 3, т. е. 6, 9, 12 и т. д.). В конце концов оставались невычеркнутыми только простые числа:
Учебники по всему предметам скачать, разработка планов уроков для учителей, Математика для 6 класса онлайн Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: