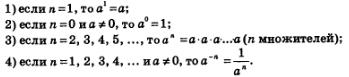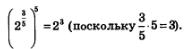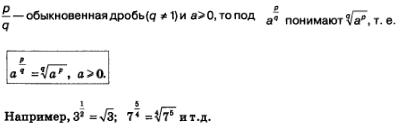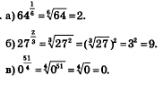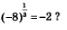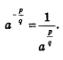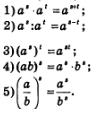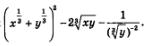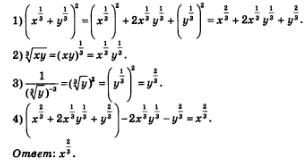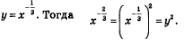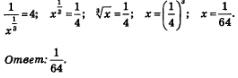|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Обобщение понятия о показателе степени
§ 43. Обобщение понятия о показателе степени
Вы умеете вычислять значение степени с любым целочисленным показателем, руководствуясь при этом следующими определениями:
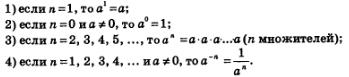
Но математики на этом не остановились, они научились работать не только с целочисленными показателями. В этом параграфе мы обсудим, какой смысл придается в математике понятию степени с дробным показателем, т.е. выясним, что означают такие символы математического языка, как 25, З-0'3 и т.д.
Зададимся вопросом: если вводить символ 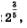 то каким математическим содержанием его наполнить? Хорошо бы, рассуждали математики, чтобы сохранялись привычные свойства степеней, например, чтобы при возведении степени в степень показатели перемножались, в частности, чтобы выполнялось следующее равенство: то каким математическим содержанием его наполнить? Хорошо бы, рассуждали математики, чтобы сохранялись привычные свойства степеней, например, чтобы при возведении степени в степень показатели перемножались, в частности, чтобы выполнялось следующее равенство:
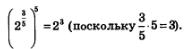
Положим 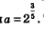 Тогда интересующее нас равенство можно переписать в виде а5=23, откуда получаем Тогда интересующее нас равенство можно переписать в виде а5=23, откуда получаем 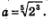 Значит, появились основания определить Значит, появились основания определить 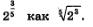
Подобные соображения и позволили математикам принять следующее определение.
Определение 1. Если
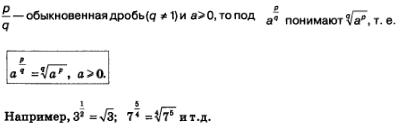
Самое любопытное, что введенное определение оказалось настолько удачным, что при нем сохранились все привычные свойства степеней, которые были доказаны для натуральных показателей: при умножении степеней с одинаковыми основаниями показатели складываются, при делении — вычитаются и т.д. Пусть, например, нам нужно выполнить умножение

Поскольку складывать дроби легче, чем применять свойства радикалов, на практике предпочитают заменять радикалы степенями с дробными показателями. Для иллюстрации этого положения вернемся к примеру 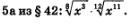 Если перейти к дробным показателям, то получим: Если перейти к дробным показателям, то получим:
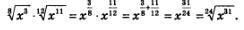
Видите, насколько быстрее и проще мы получили здесь тот же результат, что и в § 42.
Пример 1. Вычислить: 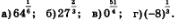
Решение.
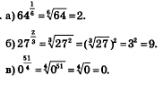
г) Это задание некорректно, поскольку нет определения степени с дробным показателем для случая отрицательного основания. Математики договорились возводить в дробные степени только неотрицательные числа (и это оговорено в определении). Так что запись вида 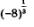 считается в математике лишенной смысла. считается в математике лишенной смысла.
Замечание. Иногда приходится слышать возражения: неверно, что запись 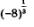 лишена смысла, ведь можно вычислить корень 3-й степени из числа -8; получится лишена смысла, ведь можно вычислить корень 3-й степени из числа -8; получится 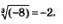 Так почему бы не считать, что Так почему бы не считать, что
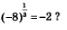
Если бы математики не запретили себе возводить в дробные степени отрицательные числа, то вот с какими неприятностями пришлось бы столкнуться:
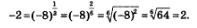
Получилось «равенство» -2 = 2. Выбирая определения, математики как раз и заботятся о том, чтобы все было точно, определенно, недвусмысленно. Поэтому в определении степени с нулевым показателем а° появилось ограничение 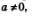 а в определении степени с положительным дробным показателем а в определении степени с положительным дробным показателем 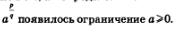
Разумеется, математики не ограничились понятием степени с положительным дробным показателем, они ввели и определение степени с отрицательным дробным показателем, используя известную идею:
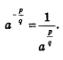
Но наличие дробного показателя заставляет сделать ограничение а>0, а наличие знаменателя заставляет сделать ограничение а= 0; в итоге приходится накладывать ограничение а > 0.
Определение 2. Если

Итак, теперь мы знаем, что такое степень с любым рациональным показателем. Справедливы следующие свойства (мы считаем, что а> 0, b> 0, s и t — произвольные рациональные числа):
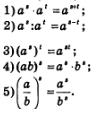
Частичные обоснования указанных свойств были сделаны выше; этим мы и ограничимся.
Пример 2. Упростить выражение:
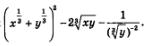
Решение.
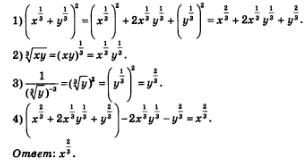
Пример 3. Решить уравнения: 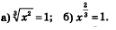
Решение: а) Возведя обе части уравнения в куб, получаем:
х2=1,
х = ±1.
б) Это практически то же самое уравнение, что и в п. а), но с одной существенной оговоркой: поскольку переменная х возводится в дробную степень, она, по определению, должна принимать только неотрицательные значения. Значит, из найденных выше двух значений х в качестве корня уравнения мы имеем право взять лишь значение х = 1.
Ответ: а) ±1; б) 1.
Пример 4. Решить уравнение: 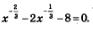
Решение. Введем новую переменную 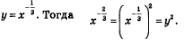
Значит, получаем квадратное уравнение относительно новой переменной у:
у2 -2у-8 = 0.
Решив это уравнение, получим: у1 =-2, у2 =4. Теперь задача сводится к решению двух уравнений:
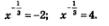
Первое уравнение не имеет корней, поскольку (напомним еще раз) область допустимых значений для переменной х в подобных случаях определяется условием х > 0. Решая второе уравнение, последовательно находим:
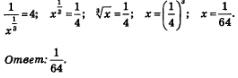
Уравнения, в которых переменная содержится под знаком корня или возводится в дробную степень, называют иррациональными. Первое знакомство с иррациональными уравнениями состоялось у вас в курсе алгебры 8-го класса, где встречались уравнения, содержащие переменную под знаком квадратного корня. В этой главе мы рассмотрели еще несколько примеров решения иррациональных уравнений — пример 2 из § 39, пример 2 из § 40 и примеры 3 и 4 из § 43.
Основные методы решения иррациональных уравнений:
— метод возведения обеих частей уравнения в одну и ту же степень;
— метод введения новых переменных;
— функционально-графический метод.
Если используется метод возведения обеих частей уравнения в одну и ту же четную степень, то возможно появление посторонних корней, значит, обязательна проверка всех найденных решений — об этом мы говорили и раньше, в курсе алгебры 8-го класса.
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|