Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Объемы. Объем прямоугольного параллелепипеда

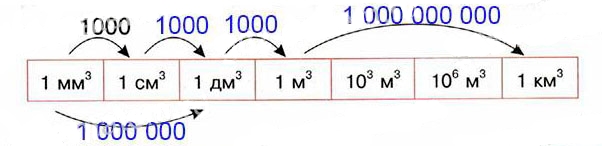
Объем параллелепипеда

Величина объема дает нам представление о том, какую часть пространства занимает интересующий нас объект, а чтобы найти объем прямоугольного параллелепипеда нужно умножить его площадь основания на высоту.

В повседневной жизни, чаще всего для измерения объема жидкости, как правило, используют такую измерительную единицу, как литр = 1дм3.

Кроме этой единицы измерения для определения объема применяют:

Параллелепипед относится к простейшим трехмерным фигурам и поэтому найти его объем не представляет никаких сложностей.

Объем параллелепипеда равен произведению его длины, ширины и высоты. Т.е. для нахождения объема прямоугольного параллелепипеда, достаточно умножить все его три измерения.

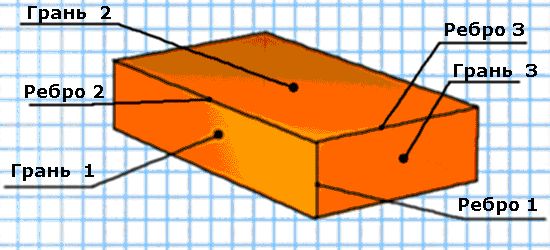
Чтобы найти объем куба, нужно взять его длину и возвести в третью степень.

Определение параллелепипеда

А теперь давайте вспомним, что же такое параллелепипед и чем он отличается от куба.

Параллелепипедом называют такую объемную фигуру, в основании которой лежит многоугольник. Поверхность прямоугольного параллелепипеда состоит из шести прямоугольников, которые являются гранями данного параллелепипеда. Поэтому логично, что параллелепипед имеет шесть граней, которые состоят из параллелограммов. Все грани этого многоугольника, которые расположены друг против друга, имеют одинаковые размеры.

Все ребра параллелепипеда и есть сторонами граней. А вот точки соприкосновения граней являются вершинами данной фигуры.

Задание:

1. Посмотрите внимательно на рисунок и скажите, что она вам напоминает?
2. Подумайте и дайте ответ, где в повседневной жизни вы можете столкнуться с такой фигурой?
3. Сколько ребер имеет параллелепипед?

Разновидности параллелепипедов

Параллелепипеды делятся на несколько разновидностей, таких как:

• Прямоугольный;
• Наклонный;
• Куб.

К прямоугольным параллелепипедам относятся те фигуры, у которых грани состоят из прямоугольников.

Если же боковые грани не являются перпендикулярными его основанию, то перед вами наклонный параллелепипед.

Такая фигура, как куб, также является параллелепипедом. Его все без исключения грани имеют форму квадратов.

Свойства параллелепипеда

Изучаемая фигура имеет ряд свойств, о которых мы сейчас с вами узнаем:

• Во-первых, противоположные грани этой фигуры равны и параллельны друг другу;

• Во-вторых, он симметричен лишь относительно средины любой без исключения своей диагонали;

• В-третьих, если взять и провести диагонали между всеми противоположными вершинами параллелограмма, то у них окажется всего одна точка пересечения.

• В-четвертых, квадрат длинны его диагонали, равен сумме квадратов 3-х его измерений.

Историческая справка

За период разных исторических эпох в разных странах использовали различные системы измерения массы, длины и других величин. Но так как это затрудняло торговые отношения между странами, а также тормозило развитие наук, то появилась необходимость иметь единую международную систему мер, которая была бы удобна для всех стран.

Метрическая система мер СИ, которая устраивала большинство стран, была разработана во Франции. Благодаря Менделееву метрическая система мер была внедрена и в России.

Но многие профессии по сей день используют свои специфические метрики, иногда это дань традициям, иногда вопрос удобства. Так, например, моряки все еще предпочитают измерять скорость в узлах, а расстояние в милях – для них это традиция. А вот ювелиры всего мира отдают предпочтение такой единице измерения, как карат – и в их случае это и традиция и удобство.

Вопросы:

1. А кто знает, сколько метров в одной миле? А что такое один узел?
2. Почему единица измерения алмазов называется «карат»? Почему ювелирам исторически удобно измерять массу в таких единицах?
3. А кто помнит, в каких единицах измеряется нефть?