|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Окружность, описанная около треугольника. Полные уроки ТЕМА УРОКА: Окружность, описанная около треугольника.
Цели урока:
|
 |
|
Окружность, описанная вокруг треугольника |
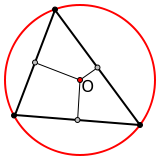
Вокруг любого треугольника можно описать окружность, притом только одну. Её центром будет являться точка пересечения серединных перпендикуляров.
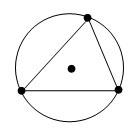
У остроугольного треугольника центр описанной окружности лежит внутри, у тупоугольного — вне треугольника, у прямоугольного — на середине гипотенузы.
 | 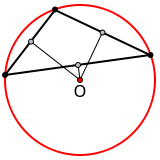 | 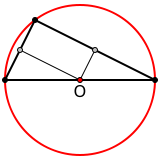 |
| Остроугольный | Тупоугольный | Прямоугольный |
Радиус описанной окружности может быть найден по формулам:
Где:
a,b,c — стороны треугольника,
α — угол, лежащий против стороны a,
S — площадь треугольника.
Файл:T.gif Теорема. Теорема о центре окружности, описанной около треугольника.
Центр окружности, описанной около треугольника, является точкой пересечения перпендикуляров к сторонам треугольника, проведенных через середины этих сторон.
Доказательство.
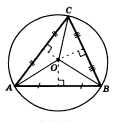
Пусть ABC – данный треугольник и O – центр окружности описанной около данного треугольника. Δ AOB – равнобедренный ( AO = OС как радиусы). Медиана OD этого треугольника одновременно является его высотой. Поэтому центр окружности лежит на прямой, перпендикулярной стороне AC и проходящей через ее середину. Так же доказывается, что центр окружности на перпендикулярах к другим сторонам треугольника.
Теорема доказана.
Рассмотрим подробнее этот случай.
Дано:
ΔABC, окр (О, ОА) - описана около ΔABC
Доказать:
т.О - точка пересечения серединных перпендикуляров к сторонам ΔABC
Доказательство:
- ΔAОC - равнобедренный, т.к. ОА=ОС (как радиусы)
- ΔAОC - равнобедренный, перпендикуляр OD - медиана и высота, т.е. т.О лежит на серединном перпендикуляре к стороне АС
- Аналогично доказывается, что т.О лежит на серединных перпендикулярах к сторонам АВ и ВС
Что и требовалось доказать.
Замечание.
Прямую, проходящую через середину отрезка перпендикулярно к нему, часто называют серединным перпендикуляром. В связи с этим иногда говорят, что центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Файл:T.gif Теорема. Теорема об окружности, описанной около треугольника. Около любого треугольника можно описать окружность.
Дано:
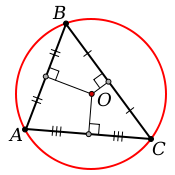
АВС — данный треугольник; О — точка пересечения серединных перпендикуляров (рис. 31).
Доказать:
О — центр окружности, вписанной в АВС.
Доказательство:
Обозначим буквой О точку пересечения серединных перпендикуляров к его сторонам и проведем отрезки ОА, ОВ и ОС. Так как точка О равноудалена от вершин треугольника АВС, то ОА=OB=ОС. Поэтому окружность с центром О радиуса ОА проходит через все три вершины треугольника и, значит, является описанной около треугольника ABC.
Замечание.
Отметим, что около треугольника можно описать только одну окружность. В самом деле, допустим, что около треугольника можно описать две окружности. Тогда центр каждой окружности равноудален от вершин треугольника и, значит, совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника, а радиус равен расстоянию от точки О до вершин треугольника. Следовательно, эти окружности совпадают.
Практическая часть.
Задача №1.
Около равнобедренного треугольника с основанием AC и углом при основании 75˚ описана окружность с центром O.
Найдите ее радиус, если площадь треугольника BOC равна 16.
Дано:
∆ ABC – равнобедренный, AC – основание, ∠ ACB = 75˚,
площадь ∆ BOC равна 16
Найти:
Радиус описанной окружности
Решение:
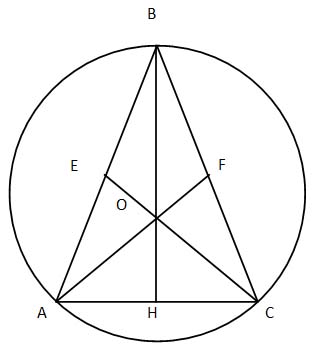
Проведем медианы AF, CE, BH
∆ ABC – равнобедренный, BH – медиана, следовательно, BH – высота, а значит ∆ HBC – прямоугольный
ﮮ HBC = 90˚ - ﮮ ACB, ﮮ HBC = 90˚ - 75˚ = 15˚
BO = OC = R, следовательно, ∆ BOC – равнобедренный, значит ﮮHBC = ﮮECB = 15˚
ﮮ COB = 180˚ - (ﮮ HBC + ﮮECB), ﮮ COB = 180˚ - (15˚ + 15˚) = 150˚
S = 1/2 ∙ BO ∙ OC ∙ sin ﮮ BOC (теорема о площади треугольника),
SBOC = 1/2 ∙ R ∙ R ∙ sin 150˚ = 1/2 ∙ R ∙ R ∙ 1/2 = 1/4 ∙ R2 ;
1/4 ∙ R2 = 16;
R2 = 16 : 1/4 = 64;
R = 8
Ответ: R = 8
Задача №2.
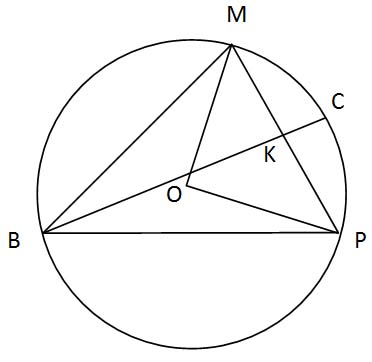
Треугольник BMP с углом B, равным 45˚, вписан в окружность радиуса 6.
Найдите длину медианы BK, если BK пересекает окружность в точке C и CK = 3.
Решение:
ﮮ MOP = 2 ﮮMBP
ﮮ MOP = 2 ∙ 45˚ = 90˚, следовательно, ∆ MOP – прямоугольный
MP2 = OM2 + OP2
MP2 = 62 + 62 = 36 + 36 = 36 ∙ 2
MP =
MK = KP = 0,5 ∙ MP
MK = KP = 0,5 ∙ =
MK ∙ KP = BK ∙ KC∙
= BK ∙ 3
BK ∙ 3 = 9 ∙ 2
BK ∙ 3 = 18
BK = 6
Ответ: BK = 6
Задача №3.
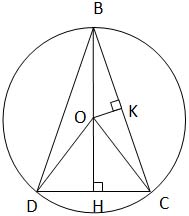
Остроугольный равнобедренный треугольник BCD с основанием CD, равным 16, вписан в окружность с центром O и радиусом 10. Найдите площадь треугольника BOC.
Решение:
Ответ: SBOC = 40
Интересный факт:
Софизмы.
Софизм – это последовательность высказывания, рассуждений, построений, содержащая скрытую ошибку, за счет чего удается сделать неверный вывод. Задача обычно заключается в том, чтобы найти ошибку в рассуждениях.
Найдите ошибку в «доказательстве» того «странного» факта, что окружность имеет два центра.
Доказательство.
Пусть даны две непараллельные прямые a и b. Из точек А и В этих прямых поставим перпендикуляры до пересечения в точке С. Через три точки А, В и С проведем окружность, пересекающую прямую а в точке М, а прямую b в точке N. По построению ∠MAC = ∠NBC = 900, значит, эти углы опираются на диаметры МС и NC построенной окружности. Середины этих диаметров – точки О1 и О2 – центры одной и той же окружности.
Ошибка в следующем:
∠MAC = ∠NBC = 900 (по построению). Эти углы являются вписанными и опирающимися на одну и туже дугу (в нашем случае, на полуокружность), поэтому точки О1 и О2 совпадают и лежат на отрезке DC (DC – биссектриса угла ADB).
Вопросы:
- Сформулируйте определение окружности и круга?
- Что такое Софизмы?
- Какая разница между диаметром и радиусом?
- Как найти радиус окружности какая описана около треугольника?
Список использованных источников:
- Урок на тему "Наглядная геометрия" Автор: Самылина Марина Валентиновна., г. Киев
- «Единый государственный экзамен 2006. Математика. Учебно-тренировочные материалы для подготовки учащихся/ Рособрнадзор, ИСОП – М.: Интеллект-Центр, 2006»
- Мазур К. И. «Решение основных конкурсных задач по математике сборника под редакцией М. И. Сканави»
- Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Э. Г. Позняк, И. И. Юдина «Геометрия, 7 – 9: учебник для общеобразовательных учреждений»
Над уроком работали:
Самылина М.В.
Постурнак С.А.
Обух Г.Н.'
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: