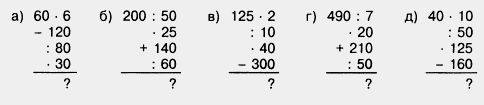|
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Окружность и круг
Окружность и круг
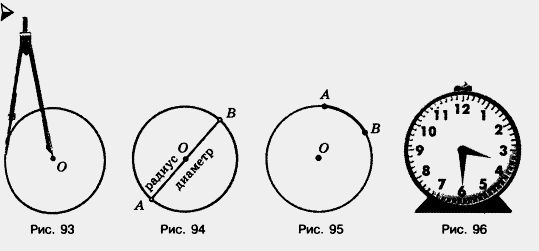
Отрезок ОА на рисунке 94 соединяет центр окружности с точкой А этой окружности. Его называют радиусом окружности (и круга). Все радиусы окружности равны друг другу. Отрезок АВ на рисунке 94 соединяет две точки окружности А и В и проходит через центр. Его называют диаметром окружности (и круга). Диаметр АВ состоит из двух радиусов: ОА и ОВ. Поэтому диаметр окружности вдвое длиннее ее радиуса.
Точки А и В на рисунке 95 делят окружность на две части. Каждую из этих частей называют дугой окружности, а точки А и В — концами этих дуг. В некоторых приборах шкалы располагаются на окружностях или дугах окружностей. На циферблате часов вся окружность разделена на 60 делений. Каждое деление соответствует одной минуте. Кроме того, циферблат часов разделен на 12 больших делений, каждое из которых соответствует одному часу (рис. 96).
а) лежат на окружности;
852. Начертите окружность и отметьте на ней три точки А, В и С. Назовите дуги, на которые эти точки делят окружность. 853. Изобразите круг, радиус которого 3 см. Отметьте точку А внутри круга и точку В вне круга. Измерьте расстояние от центра круга до точки А и до точки В. Сравните эти расстояния с радиусом круга. Соедините точки А и В отрезком. Пересекается ли он с окружностью? 854. Начертите окружность с центром в точке О и радиусом 3 см 5 мм. Проведите прямую, которая пересекает окружность в точках М и К. На каком расстоянии от центра окружности находятся эти точки? 855. Начертите отрезок CD9 равный 5 см. Проведите окружность с центром С и радиусом 3 см, а также другую окружность с центром D и радиусом 4 см. Обозначьте точки пересечения окружностей буквами А и В. Чему равны длины отрезков AC, CB> DA и BD? 856. Начертите отрезок МР, равный 6 см. Найдите две точки А и Б, которые находились бы на расстоянии 4 см от точки М и 5 см от точки Р.
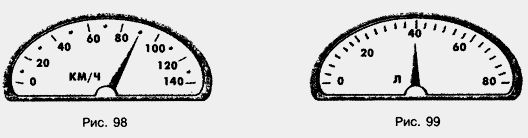
858. На рисунке 99 изображена шкала прибора, показывающего, сколько литров бензина осталось в баке автомобиля. Сколько литров бензина сейчас в баке? На сколько делений и в какую сторону передвинется стрелка прибора, если: а) в бензобак нальют еще 20 л бензина; 859. Какое время показывают часы на рисунке 96? Какое время будут показывать часы, если минутную стрелку передвинуть: а) назад на 3 больших деления; б) вперед на 20 малых делений? 860. Вычислите устно:
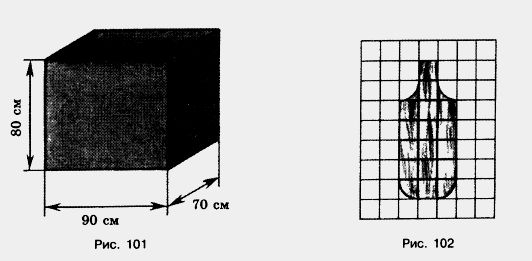
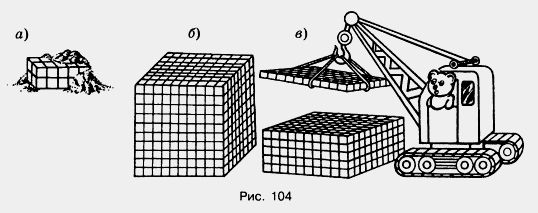
862. Укажите координаты точек Л, Б, С и D, если М(10) (рис. 100). Сравните координаты точек В и С; С и D. 863.Сколько сантиметров: а) в четверти метра; 864. Сколько килограммов: а) в десятой доле центнера; в) в двадцатой доле центнера; 865. Представьте себе, что один куб с ребром 1 дм разрезали на кубики с ребром 1 см и из этих маленьких кубиков сложили башню, поставив их один на другой. Второй куб с ребром 1 дм разрезали на кубики с ребром 1 мм и из этих кубиков так же сложили башню. Какая из этих башен выше? Во сколько раз? 866. Проверьте, справедливы ли равенства: 13 + 23 = (1 + 2)2; 13 + 23 + З3 + 43 = (1 + 2 + 3 + 4)2. Попробуйте рассказать, какова в этих равенствах зависимость между квадратами и кубами чисел. Проверьте, выполняется ли это свойство для пяти, шести чисел. 867. Найдите объем и площадь наружной поверхности бака без крышки, изображенного на рисунке 101. Сколько понадобится краски, чтобы покрасить этот бак снаружи и изнутри, если на покраску 1 дм2 нужно 2 г краски? Сколько литров бензина можно влить в этот бак? 868. Сторона одного куба 9 см, а другого 5 см. На сколько объем первого куба больше объема второго? На сколько площадь поверхности первого куба больше площади поверхности второго? 869. Найдите площадь фигуры, изображенной на рисунке 102. Площадь одной клетки 25 мм2.
871. Решите задачу: 1) На крыше дома сидели голуби. Когда на крышу сели еще 15 голубей, а с нее улетели 18 голубей, то на крыше стало 16 голубей. Сколько голубей сидело на крыше первоначально? 2) Когда от товарного состава отцепили 6 вагонов, а прицепили к нему 19 вагонов, в нем стало 50 вагонов. Сколько вагонов было в составе первоначально? 872. Выполните действия: 1) (1 445 561 : 3587 - 208) • 356 - 3580; 873. В старину часто пользовались солнечными часами, они известны более 3000 лет. В солнечных часах время определяется по положению тени от наклонного стержня на циферблате (циферблат и стержень располагали так, чтобы в полдень тень от стержня была направлена на отметку 12 ч). Подумайте, что общего у солнечных часов (рис. 103) с современными, в чем их достоинства и недостатки. 874. Начертите круг с центром А и радиусом 2 см. Отметьте две точки: а) лежащие на окружности; 875. Отметьте две точки А и В так, чтобы АВ = 3 см. С помощью циркуля постройте еще три точки С, D и Е, которые находились бы от точки А на расстоянии 3 см. 876. Отметьте две точки К и Р так, чтобы КР = 6 см. Постройте окружность с центром К и радиусом 5 см и окружность с центром Р и радиусом 4 см. Пересекаются ли эти окружности? 877. Отметьте точки О и Е так, чтобы ОЕ = 8 см. Постройте окружность с центром О и радиусом 2 см и окружность с центром Е и радиусом 4 см. Пересекаются ли эти окружности? 878. Решите уравнение: а) (х - 152) • 59 = 6018; г) 51 815 : (р - 975) = 1205; 879. Выполните деление с остатком числа 987 654 на 391.
881. Масса 1 л бензина 650 г. В бензобак автомобиля входит 95 л бензина. Какова масса бензина в полном баке этой автомашины? 882. По формуле а = bq + г найдите число а, если делитель b равен 81, неполное частное q равно 561 и остаток r равен 23. 883. Найдите значение выражения: а) 507 • 664 - 296 085; в) 123 + 53 • 4;
Материалы по математике за 5 класс скачать, конспект по математике , учебники и книги скатать бесплатно, школьная программа онлайн
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: