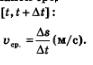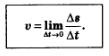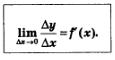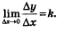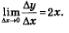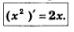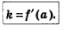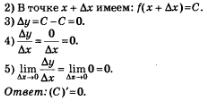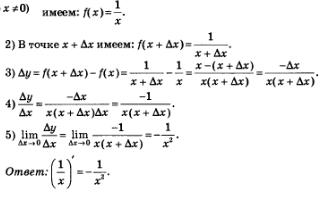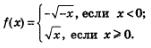|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Определение производной
§ 32. Определение производной
1. Задачи, приводящие к понятию производной
Часто бывает так, что, решая задачи, очень далекие друг от друга по содержанию, мы приходим к одной и той же математической модели. Сила математики состоит в том, что она разрабатывает способы оперирования с той или иной математической моделью, которыми потом пользуются в других областях знаний. Вы умеете работать со многими математическими моделями — уравнениями, неравенствами, системами уравнений, системами неравенств и др. В этом параграфе речь пойдет о принципиально новой для вас математической модели. Сначала рассмотрим две различные задачи, физическую и геометрическую, процесс решения которых как раз и приводит к возникновению новой математической модели.
Задача 1 (о скорости движения). По прямой, на которой заданы начало отсчета, единица измерения (метр) и направление, движется некоторое тело (материальная точка). Закон движения задан формулой s=s (t), где t — время (в секундах), s (t) — положение тела на прямой (координата движущейся материальной точки) в момент времени t по отношению к началу отсчета (в метрах). Найти скорость движения тела в момент времени t (в м/с).
Решение. Предположим, что в момент времени t тело находилось в точке М(рис. 114), пройдя путь от начала движения ОМ = s{t). Дадим аргументу t привращение 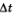 и рассмотрим момент времени и рассмотрим момент времени 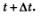 Координата материальной точки стала другой, тело в этот момент будет находиться в точке Координата материальной точки стала другой, тело в этот момент будет находиться в точке 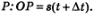
Значит, за 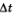 секунд тело переместилось из точки М в точку Р, т.е. прошло путь МР. Имеем: секунд тело переместилось из точки М в точку Р, т.е. прошло путь МР. Имеем: 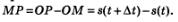
Полученную разность мы назвали в § 31 приращением функции: 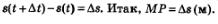

Путь 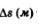 тело прошло за тело прошло за 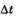 секунд. Нетрудно найти среднюю скорость секунд. Нетрудно найти среднюю скорость 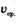 движения тела за промежуток времени движения тела за промежуток времени
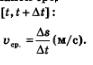
А что такое скорость v (t) в момент времени t (ее называют иногда мгновенной скоростью)? Можно сказать так: это средняя скорость движения за промежуток времени 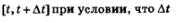 выбирается все меньше и меньше; иными словами, при условии, что выбирается все меньше и меньше; иными словами, при условии, что 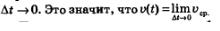
Подводя итог решению задачи 1, получаем:
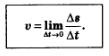
Прежде чем сформулировать вторую задачу и приступить к ее решению, обсудим вопрос, что следует понимать под касательной к плоской кривой. Термином «касательная» мы уже пользовались (на интуитивном уровне) в курсе алгебры 7—9-го классов. Например, мы говорили, что парабола у = х2 касается оси х в точке х=0 или, что то же самое, ось х является касательной к параболе у = х2 в точке х=0 (рис. 115). Иделоне в том, что ось х и парабола имеют одну общую точку. Ведь ось у тоже имеет с параболой у = х2 одну общую точку, однако у вас не возникнет желания назвать ось у касательной к параболе. Обычно касательную определяют следующим образом.
Дана кривая Ь (рис. 116), на ней выбрана точка М. Возьмем еще одну точку на кривой, причем достаточно близкую к М, — точку Р. Проведем секущую МР. Далее будем приближать точку Р по кривой Ь к точке М. Секущая МР будет изменять свое положение, она как бы поворачивается вокруг точки М. Часто бывает так, что можно обнаружить в этом процессе прямую, представляющую собой некое предельное положение секущей; эту прямую — предельное положение секущей — называют касательной к кривой Ь в точке М.
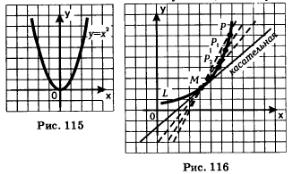
Поставьте эксперимент: возьмите параболу у = х2, проведите секущую ОР, где О — вершина параболы, Р — текущая точка. Возьмите точку Р поближе к О, проведите вторую секущую. Возьмите точку Р еще ближе к О, проведите третью секущую и т.д. Вы обнаружите, что предельным положением этих секущих будет ось х — это и есть касательная к параболе в ее вершине (что соответствует нашим интуитивным представлениям).
Задача 2 (о касательной к графику функции). Дан график функции у = f(х). На нем выбрана точка М(а; f(а)), в этой точке к графику функции проведена касательная (мы предполагаем, что она существует). Найти угловой коэффициент касательной.
Решение. Дадим аргументу приращение Ах и рассмотрим на графике (рис. 117) точку Р с абсциссой 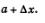 . Ордината точки Р равна . Ордината точки Р равна 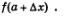 Угловой коэффициент секущей МР, т.е. тангенс угла между секущей и осью х, вычисляется по формуле Угловой коэффициент секущей МР, т.е. тангенс угла между секущей и осью х, вычисляется по формуле
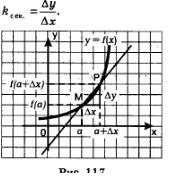
Если мы теперь устремим Ах к нулю, то точка Р начнет приближаться по кривой к точке М. Касательную мы охарактеризовали как предельное положение секущей при этом приближении. Значит, естественно считать, что угловой коэффициент касательной 
Используя приведенную выше формулу для
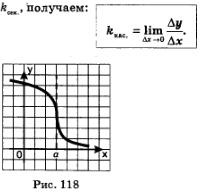
Замечание. В приведенном решении задачи 2 упущен случай, когда касательная перпендикулярна оси абсцисс (см., например, рис. 118). Уравнение такой прямой имеет вид х = а, об угловом коэффициенте говорить в этом случае некорректно, поскольку он не существует.
Подведем итоги. Две различные задачи привели в процессе решения к одной и той же математической модели — пределу отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю. Многие задачи физики, химии, экономики и т.д. приводят в процессе решения к такой же модели. Значит, эту математическую модель надо специально изучить, т.е.:
а) присвоить ей новый термин;
б) ввести для нее обозначение;
в) исследовать свойства новой модели.
Этим мы и займемся в следующем пункте.
2. Определение производной
Определение 1. Пусть функция у =f(х) определена в конкретной точке х и в некоторой ее окрестности. Дадим аргументу х приращение f(х), такое, чтобы не выйти из указанной окрестности. Найдем соответствующее приращение функции  Если существует предел этого отношения при условии Если существует предел этого отношения при условии 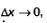 то указанный предел называют производной функции у = f(х) в точке х и обозначают f'(х). то указанный предел называют производной функции у = f(х) в точке х и обозначают f'(х).
Итак,
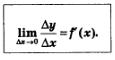
Для обозначения производной часто используют символ у'.
Отметим, что у'=f'(х) — это новая функция, но, естественно, связанная с функцией у = f(x), определенная во всех таких точках х, в которых существует указанный выше предел. Эту функцию называют так: производная функции у =f(х).
В примере 6 § 31 мы доказали, что для линейной функции у =кх + m справедливо равенство: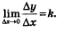
Это означает, что у'=к или, подробнее,

В примере 7 § 31 мы доказали, что для функции у = х2 справедливо равенство 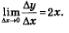
Это означает, что у'=2х или подробнее,
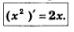
Рассмотренные в п. 1 задачи 1 и 2 позволяют истолковать производную с физической и геометрической точек зрения.
Физический (механический) смысл производной состоит в следующем. Если s(t) — закон прямолинейного движения тела, то производная выражает мгновенную скорость в момент времени t.
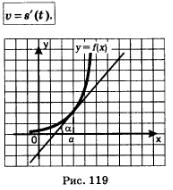
На практике во многих отраслях науки используется обобщение полученного равенства: если некоторый процесс протекает по закону s =s (t), то производная s'(t) выражает скорость протекания процесса в момент времени t.
Геометрический смысл производной состоит в следующем. Если к графику функции у = f(х) в точке с абсциссой х=а можно провести касательную, непараллельную оси у, то f'(а) выражает угловой коэффициент касательной (рис. 119):
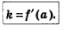
Поскольку к =tga, то верно равенство f'(а) =1tg а (рис. 119).
А теперь истолкуем определение производной с точки зрения приближенных равенств. Пусть функция у = f(х) имеет производную в конкретной точке х:
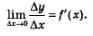
Это означает, что в достаточно малой окрестности точки х выполняется приближенное равенство: 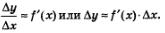
Содержательный смысл полученного приближенного равенства заключается в следующем: приращение функции «почти пропорционально» приращению аргумента, причем коэффициентом пропорциональности является значение производной (в заданной точке х). Например, для функции у = х2 справедливо приближенное равенство 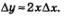
Если внимательно прочитать определение производной, то мы обнаружим, что в нем заложен алгоритм отыскания производной. Сформулируем его.

Пример 1. Найти производную постоянной функции у =С.
Решение. Воспользуемся алгоритмом отыскания производной.
1) Для фиксированного значения х имеем: f (х) = С.
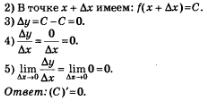
Пример 2. Найти производную функции 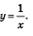 . .
Решение. Воспользуемся алгоритмом отыскания производной.
1) Для фиксированного значения х (разумеется, мы полагаем, что
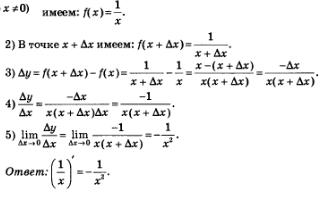
Если функция у = f(х) имеет производную в точке х, то ее называют дифференцируемой в точке х. Процедуру отыскания производной функции у = f(x) называют дифференцированием функции у = f(x). Эти термины имеют глубокий математический смысл, но мы говорить о них не будем (нам не хватает теоретических знаний).
Обсудим такой вопрос: как связаны между собой те два достаточно тонких свойства функций, которые мы обсудили в этом и в предыдущем параграфах, — непрерывность и дифференцируемость функции в точке.
Пусть функция у = f(х) дифференцируема в точке х. Тогда к графику функции в точке М(х, f(х)) можно провести касательную, причем, напомним, угловой коэффициент касательной равен f'(x). Но тогда
график не может «разрываться» в точке М, т.е. функция обязана быть непрерывной в точке х.
Это были рассуждения «на пальцах». Приведем несколько более строгие рассуждения. Если функция y = f(x) дифференцируема в точке х, то выполняется приближенное равенство 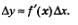 Если в Если в
этом равенстве 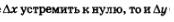 будет стремиться к нулю, а это и есть условие непрерывности функции в точке (см. п. 3 в § 31). будет стремиться к нулю, а это и есть условие непрерывности функции в точке (см. п. 3 в § 31).
Итак, если функция дифференцируема в точке х, то она и непрерывна в этой точке.
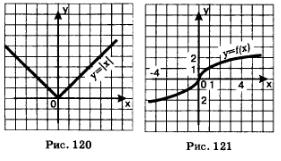
Обратное утверждение неверно. Смотрите: функция У=\х\ непрерывна везде, в частности, в точке х =0 (рис. 120), но касательной к графику функции в «точке стыка» (0; 0) не существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производной.
А вот еще один пример. На рис. 121 изображен график кусочной функции у = f(х), где
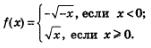
Функция непрерывна на всей числовой прямой, в том числе в точке х=0. И касательная к графику функции существует в любой точке, в том числе в точке х=0. Но в точке х=0 касательная совпадает с осью у, т.е. перпендикулярна оси абсцисс, ее уравнение имеет вид х=0. Углового коэффициента у такой прямой нет, значит, не существует и f'(0).
Итак, мы познакомились с новым свойством функции — дифференцируе-мостью. Формальные определения тех или иных свойств функции — дело, конечно, хорошее, но у нас всегда были приемы «считывания информации» о наличии того или иного свойства функции по ее графику. Например, если график был сплошным, мы говорили, что функция непрерывна. А как по графику сделать вывод о дифференцируемости функции?
Ответ фактически получен выше. Если в некоторой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция дифференцируема. Если в некоторой точке касательная к графику функции не существует или она перпендикулярна оси абсцисс, то в этой точке функция недифференцируема. Так, по графику функции, изображенному на рис. 122, можно сделать вывод: функция непрерывна всюду, кроме точки х =а; функция дифференцируема всюду, кроме точек х=а,х=b — здесь касательная не существует, х—с — здесь касательная параллельна оси у.
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|