|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Определение четырехугольника. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
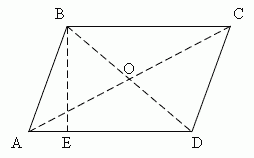
Неевклидова геометрияНеевклидова геометрия, геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов (1825) явилось значительным событием в истории мысли, ибо послужило первым шагом на пути ктеории относительности. Из этих пересмотренных постулатов следовало, что сумма углов треугольника, равная 180° в евклидовой геометрии, больше 180° в эллиптической геометрии и меньше 180° в гиперболической геометрии. ЧетырёхугольникЧетырёхугольник — это многоугольник, содержащий четыре вершины и четыре стороны. Четырёхугольник, геометрическая фигура — многоугольник с четырьмя углами, а также всякий предмет, устройство такой формы. Две несмежные стороны четырехугольника называются противоположными . Две вершины, не являющиеся соседними, называются также противоположными. Четырехугольники бывают выпуклые (как ABCD) и
Виды четырёхугольников
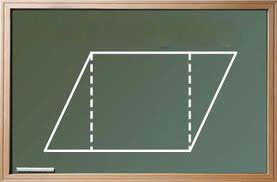
ПараллелограммПараллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны. Параллелогра́мм (от греч. parallelos — параллельный и gramme — линия) т. е. лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Свойства параллелограмма
Признаки параллелограмма Четырехугольник является параллелограммом, если:
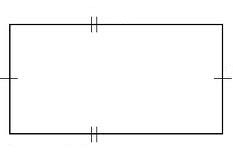
ПрямоугольникПрямоугольником называется параллелограмм, у которого все углы прямые. Свойства прямоугольника.
Параллелограмм является прямоугольником, если:
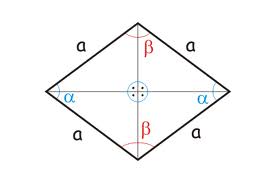
РомбРомбом называется параллелограмм, у которого все стороны равны.
Признаки ромба Параллелограмм является ромбом, если:
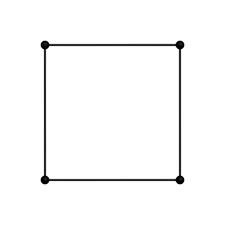
КвадратКвадратом называется прямоугольник, у которого все стороны равны. Свойства квадрата
Признаки квадрата
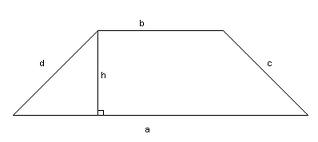
ТрапецияТрапецией называется четырехугольник, у которого две противолежащие стороны параллельны, а две другие непараллельны. Параллельные стороны трапеции называются ее основаниями, а непараллельные стороны — боковыми сторонами. Отрезок, соединяющий середины боковых сторон, называется средней линией. Трапеция называется равнобедренной (или равнобокой), если ее боковые стороны равны. Трапеция, один из углов которой прямой, называется прямоугольной.
Свойства трапеции
Признаки трапеции.
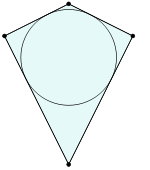
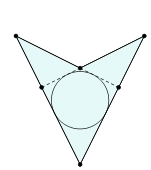
ДельтоидДельтоид — четырёхугольник, обладающий двумя парами сторон одинаковой длины. В отличие от параллелограмма, равными являются не противоположные, а две пары смежных сторон. Дельтоид имеет форму, похожую на воздушного змея. Дельтоид выпуклый Дельтоид невыпуклый Свойства
Частные случаи
Интересный фактВозникновение геометрии восходит к глубокой древности и было обусловлено практическими потребностями человеческой деятельности (необходимостью измерения земельных участков, измерения объемов различных тел и т. д.). Простейшие геометрические сведения и понятия были известны еще в Древнем Египте. В этот период геометрические утверждения формулировались в виде правил, даваемых без доказательств. С VII века до н. э. по I век н. э. геометрия как наука бурно развивалась в Древней Греции. В этот период происходило не только накопление различных геометрических сведений, но и отрабатывалась методика доказательств геометрических утверждений, а также делались первые попытки сформулировать основные первичные положения (аксиомы) геометрии, из которых чисто логическими рассуждениями выводится множество различных геометрических утверждений. Уровень развития геометрии в Древней Греции отражен в сочинении Евклида «Начала». В этой книге впервые была сделана попытка дать систематическое построение планиметрии на базе основных неопределяемых геометрических понятий и аксиом (постулатов). Особое место в истории математики занимает пятый постулат Евклида (аксиома о параллельных прямых). Долгое время математики безуспешно пытались вывести пятый постулат из остальных постулатов Евклида и лишь в середине XIX века благодаря исследованиям Н. И. Лобачевского, Б. Римана и Я. Бойяи стало ясно, что пятый постулат не может быть выведен из остальных, а система аксиом, предложенная Евклидом, не единственно возможная. «Начала» Евклида оказали огромное влияние на развитие математики. Эта книга на протяжении более чем двух тысяч лет была не только учебником по геометрии, но и служила отправным пунктом для очень многих математических исследований, в результате которых возникли новые самостоятельные разделы математики. Систематическое построение геометрии обычно производится по следующему плану:
Вопросы
Список использованных источников
Над уроком работали Марина Александровна. Потурнак С.А. Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: