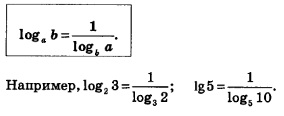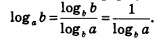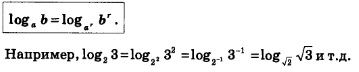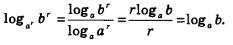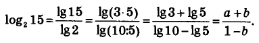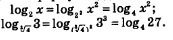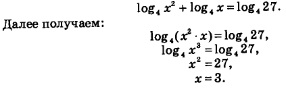|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Переход к новому основанию логарифма
§ 53. Переход к новому основанию логарифма
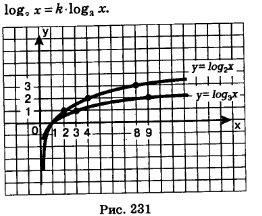
Логарифмических функций бесконечно много: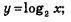 и т.д. Возникает вопрос, как они связаны между собой? Есть ли, например, какая-то связь между функциями у=log2 х и y=log3 x? На рис. 231 изображены графики функций у=log2 х и у=log3 х. Не кажется ли вам, что график первой функции получается из графика второй функции растяжением от оси х с некоторым коэффициентом к >1. Если наше геометрическое наблюдение верно, то должно выполняться равенство: и т.д. Возникает вопрос, как они связаны между собой? Есть ли, например, какая-то связь между функциями у=log2 х и y=log3 x? На рис. 231 изображены графики функций у=log2 х и у=log3 х. Не кажется ли вам, что график первой функции получается из графика второй функции растяжением от оси х с некоторым коэффициентом к >1. Если наше геометрическое наблюдение верно, то должно выполняться равенство:
Так ли это? На все поставленные вопросы мы ответим в этом параграфе. Теоретической основой для ответа является следующая теорема.

Теперь нетрудно ответить на поставленный выше вопрос: как связаны между собой различные логарифмические функции? Рассмотрим две логарифмические функции у =log2 х и у =log3 х, графики которых изображены на рис. 231. Имеем:
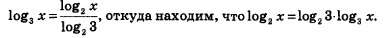
Таким образом, наша догадка подтвердилась: действительно, справедливо соотношение
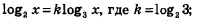 ; ;
подтвердилась и наша догадка о том, что в данном случае к > 1, поскольку log2 3 > 1.
Аналогичные формулы связывают и другие логарифмические функции. Например, справедливы соотношения:
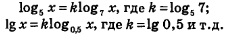
Рассмотрим два важных частных случая формулы перехода к новому основанию логарифма, два следствия из доказанной теоремы.
Следствие 1. Если а и b положительные и отличные от 1 числа, то справедливо равенство:
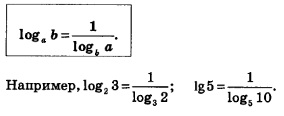
Доказательство. Положив в формуле (1) с =Ь, получим:
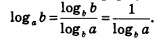
Следствие 2. Если а и b — положительные числа, причем 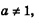 , то для любого числа , то для любого числа 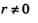 справедливо равенство: справедливо равенство:
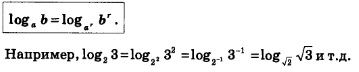
Доказательство. Перейдем в выражении 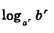 к логарифмам по основанию а: к логарифмам по основанию а: 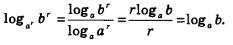
Пример 1. Дано:
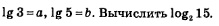
Решение.
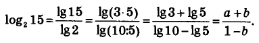
Пример 2. Решить уравнение:
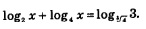
Решение. Перейдем во всех логарифмах к одному основанию 4. Для этого дважды воспользуемся формулой, доказанной в следствии 2:
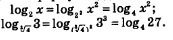
Теперь заданное уравнение можно переписать в более простой форме:
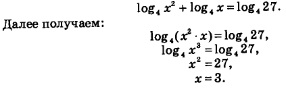
Ответ: х = 3.
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|