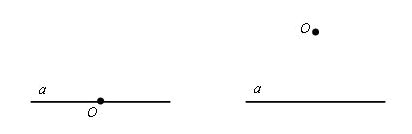|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Перпендикулярные прямые. Полные уроки
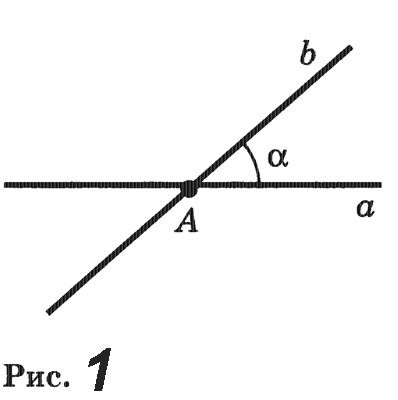
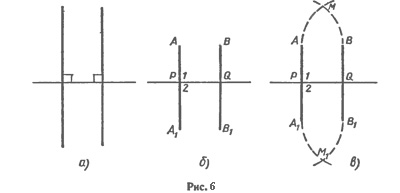
Определение перпендикулярных прямыхПерпендикулярные прямые. Пусть а и b — прямые, пересекающиеся в точке А (рис. 1). Каждая из этих прямых точкой А делится на две полупрямые. Полупрямые одной прямой образуют с полупрямыми другой прямой четыре угла. Пусть альфа — один из этих углов. Тогда любой из остальных трех углов будет либо смежным с углом альфа, либо вертикальным с углом альфа.
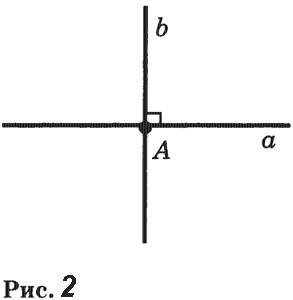
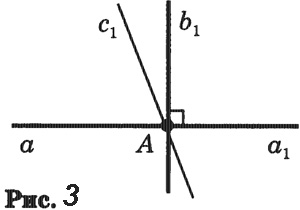
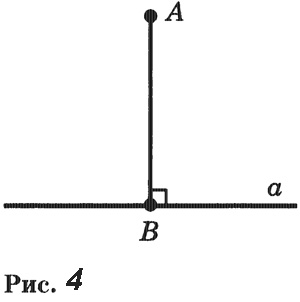
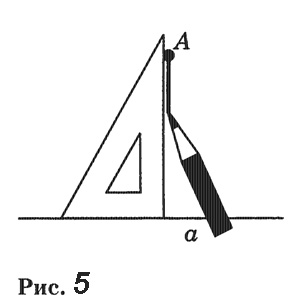
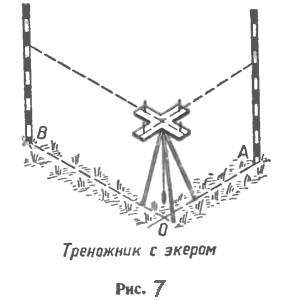
Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну. Доказательство. Допустим, что существует другая прямая, проходящая через точку А и перпендикулярная прямой а. Обозначим через с1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b2. Углы (a1b1) и (a1c1), равные каждый 90°, отложены в одну полуплоскость от полупрямой а1. Но от полупрямой а1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не может быть другой прямой, проходящей через точку А и перпендикулярной прямой а. Теорема доказана. Определение. Перпендикуляром к данной прямой называется отрезок прямой, перпендикулярной данной, который имеет одним из своих концов их точку пересечения. Этот конец отрезка называется основанием перпендикуляра. Для построения перпендикуляра пользуются чертежным угольником (рис. 5). Две пересекающиеся прямые называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла. Перпендикулярность прямых АС и ВD обозначается так: АС ⊥ ВD (читается: «Прямая АС перпендикулярна к прямой ВD»). Построение прямых углов на местностиДля построения прямых углов на местности применяют специальные приборы, простейшим из которых является экер. Экер представляет собой два бруска, расположенных под прямым углом и укрепленных на треножнике (рис. 7). На концах брусков вбиты гвозди так, что прямые, проходящие через них, взаимно перпендикулярны. Чтобы построить на местности прямой угол с заданной стороной ОА, устанавливают треножник с экером так, чтобы отвес находился точно над точкой О, а направление одного бруска совпало с направлением луча ОА. Совмещение этих направлений можно осуществить с помощью вехи, поставленной на луче. Затем провешивают прямую линию по направлению другого бруска (прямая ОВ на рисунке 7). Получается прямой угол АОВ.
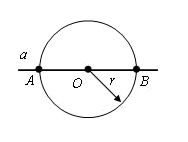
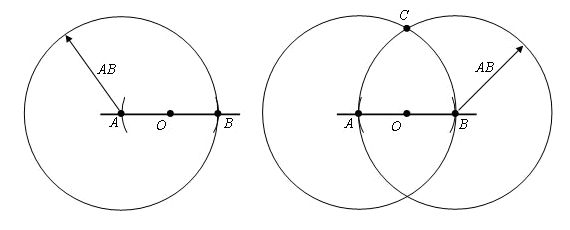
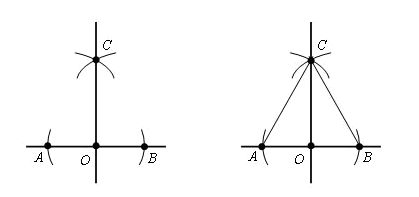
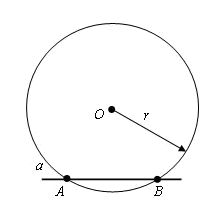
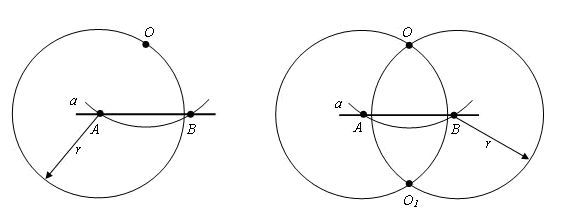
Задание. По горизонтали: Интересная задачаЕсть такая задача: Построение перпендикулярной прямойСейчас мы с вами с помощью циркуля попробуем построить перпендикулярную прямую. Для этого у нас есть точка О и прямая а. На первом рисунке изображена прямая на которой лежит точка О, а на втором данная точка не лежит на прямой а. Теперь давайте по отдельности рассмотрим эти оба варианта. 1-й вариантВначале мы берем циркуль, ставим его в центр точки О и чертим окружность с произвольным радиусом. Теперь мы видим, что данная окружность пересекает прямую а в двух точках. Пускай это будут точки А и В. Далее, мы берем и проводим окружности из точек А и В. Радиус этих окружностей будет АВ, а вот точка С будет точкой пересечения этих окружностей. Если вы помните, то в самом начале мы с вами получили точки А и В, когда чертили окружность и брали произвольный радиус. В итоге мы видим, что искомая перпендикулярная прямая проходит через точки С и О. Доказательство Для данного доказательства нас нужно провести отрезки AC и CB. И мы видим, что образовавшиеся треугольники равны: Δ ACO = Δ BCO, это следует из третьего признака равенства треугольников, то есть у нас выходит, что AO = OB, AC = CB, а СО общая по построению. Образовавшиеся углы ∠ COA и ∠ COB равны и оба имеют величину, равную 90 °. Из этого следует, что прямая CO перпендикулярна AB. Отсюда мы можем сделать вывод, что углы, образованные при пересечении двух прямых являются перпендикулярными в том случае, если хотя бы один из них перпендикулярен, а это значит, что такой угол равен 90 градусам и является прямым. 2-й вариантА сейчас давайте рассмотрим вариант построения перпендикулярной прямой, где данная точка не лежит на прямой а. В этом случае мы с помощью циркуля из точки О проводим окружность с таким радиусом, чтобы эта окружность пересекала прямую а. А точки А и В пускай будут точками пересечения этой окружности с данной прямой а. Далее, мы берем такой же радиус, но проводим окружности, центром которых будут точки A и B. Смотрим на рисунок и видим, что у нас появилась точка О1, которая также является точкой пересечения окружностей и лежит в полуплоскости, но отличной от той, в которой находится точка О. Следующее, что мы сделаем, так это через точки O и O1проведем прямую. Это и будет та перпендикулярная прямая, которую мы искали. Доказательство Припустим, что точкой пересечения прямых OO1 и AB является точка С. Тогда треугольники AOB и BO1A равны по третьему признаку равенства треугольников и AO = OB = AO1 = O1B, а АВ является общей по построению. Из этого следует, что углы OAС и O1AC равны. Треугольники OAC и O1AC, следуя из первого признака равенства треугольников AO равняется AO1, а по построению, углы OAС и O1AC равны при общей AС. Следовательно, что угол OСA равен углу O1CA, но а так как они смежные, то значит прямые. Поэтому, делаем вывод, что OC является перпендикуляром, который опущенный из точки O на прямую a. Вот так, только с помощью циркуля и линейки, можно легко построить перпендикулярные прямые. И не важно, где находится точка, через которую должен проходит перпендикуляр, на отрезке или вне этого отрезка, главное в этих случаях верно найти и обозначить первоначальные точки А и В. Вопросы:
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: