|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Перпендикуляр и наклонная. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
Вступительное словоНе для кого не секрет что вся элементарная геометрия пришла к нам в основном с Египта и Греции. В далекие и древние времена геометрия использовалась как наука для измерения земли, а также очень тесно при строительстве. Все теоремы, законы и аксиомы выводили и доказывали что бы облегчить измерительные или строительные работы. Сегодняшняя тема была очень важна для людей того времени так как перпендикуляр и наклонная основные ориентиры при работе такого типа.
Техника строительства Великих пирамид по ГеродотуНашим единственным письменным источником, в котором описывается процесс строительства пирамид, служит II книга «Истории» Геродота, посетившего Египет ок. 450 г. до н. э. Не говоря на языке египтян, Геродот должен был делать записи со слов греческих поселенцев, проживавших в стране, а также — через переводчиков — со слов представителей египетского жречества. О том, как строили Великие пирамиды две тысячи лет назад до него, ему определённо было трудно узнать, поскольку это вряд ли было известно и самим египтянам. Одни были обязаны перетаскивать к Нилу огромные глыбы камней из каменоломен в Аравийских горах (через реку камни перевозили на кораблях), а другим было приказано тащить их дальше до так называемых Ливийских гор. Сто тысяч людей выполняло эту работу непрерывно, сменяясь каждые три месяца. Десять лет пришлось измученному народу строить дорогу, по которой тащили эти каменные глыбы, — работа, по-моему, едва ли не столь же огромная, как и постройка самой пирамиды. Сооружение же самой пирамиды продолжалось двадцать лет.
Другие теории изготовления блоков и их установкиСуществует также теория о том, что сами блоки из которых состоит пирамида, были изготовлены при помощи опалубки. На предыдущем ярусе устанавливалась опалубка прямоугольной формы, в которую затем заливался растворообразный состав. Застывший блок сам служил опалубкой для следующих блоков растущего яруса. Составные части раствора относительно легко могли быть доставлены силами многочисленных рабов без применения сложной техники. Такая теория хорошо объясняет идеальную подгонку стен отдельных блоков.
Альтернативные гипотезыРяд авторов выдвигают гипотезы постройки пирамид другими развитыми цивилизациями, либо земными, которые потом исчезли, либо инопланетными. Также одним из обществ египтологов-любителей была выдвенута теория, согласно которой огромные каменные глыбы перемещались с помощью воздушных змеев. Египтологи не рассматривают такие гипотезы всерьёз.
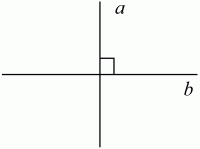
Перпендикуляр и наклоннаяИ так начнем с простейшего и давайте повторим что такое перпендикуляр и наклонная. Перпендикулярные прямыеОпределение. Две прямые называются перпендикулярными, если они пересекаются под прямым углом. Перпендикулярность прямых обозначается знаком ⊥ Запись а ⊥ b читается: Прямая а перпендикулярна прямой b.
Теорема. Через каждую точку прямой можно провести перпендикулярную ей прямую, и только одну.
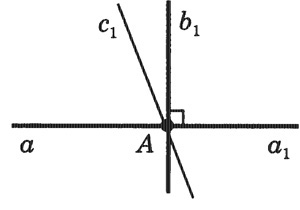
Допустим, что существует другая прямая, проходящая через точку А и перпендикулярная прямой а. Обозначим через с1 полупрямую этой прямой, лежащую в одной полуплоскости с лучом b2. Углы (a1b1) и (a1c1), равные каждый 90°, отложены в одну полуплоскость от полупрямой а1. Но от полупрямой а1 в данную полуплоскость можно отложить только один угол, равный 90°. Поэтому не может быть другой прямой, проходящей через точку А и перпендикулярной прямой а. Теорема доказана.
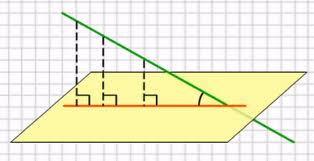
Наклонные прямыеНаклонная прямая — это плоская поверхность, установленная под углом, отличным от прямого или нулевого, к горизонтальной поверхности.
Наклонная плоскость — один из широко известных простых механизмов. Пандусы, или наклонные плоскости, широко использовались при строительстве ранних каменных сооружений, дорог и акведуков. Также они применялись при штурме военных укреплений. Эксперименты с наклонными плоскостями помогли средневековым физикам (таким, как Галилео Галилей) изучить законы природы, связанные с гравитацией, массой, ускорением и т. д. Простейшие механизмы — устройства, служащие для преобразования силы. Представляют собой элементы более сложных механизмов. Некоторые из простейших механизмов появились в глубокой древности. Простейшие механизмы какие работают с помощью наклонной плоскости:
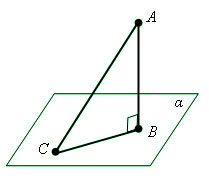
Перпендикуляр и наклоннаяПерпендикуляром, опущенным из данной точки данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра. Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной. AB – перпендикуляр к плоскости α.
Задача №1Условие: Опустим перпендикуляр. Можете ли Вы опустить из данной точки A вне прямой l опустить перпендикуляр на эту прямую, проводя не более трех линий? (Третьей прямой должен быть перпендикуляр). Решение: Выбираем любую точку на заданной прямой l, задаемся радиусом к точке А и проводим окружность. Повторяем те же действия для второй окружности, пересечение окружностей друг с другом дает нам перпендикуляр к заданной прямой. Действительно проведено три линии: две окружности и вертикальная прямая AA1.
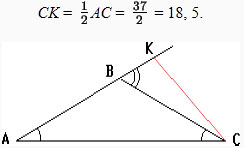
Задача №2Условие: В равнобедренном треугольнике ABC с основанием AC, равным 37, внешний угол при вершине B равен 60o. Найдите расстояние от вершины C до прямой AB. Подсказка: Катет, лежащий против угла в 30o, равен половине гипотенузы. Решение: Пусть K — основание перпендикуляра, опущенного из точки C на прямую AB. Поскольку ∠А + ∠С = 60о , ∠А = ∠С ∠А = 30о
Ответ: 18,5.
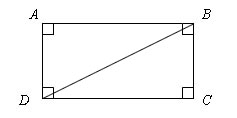
Задача №3Условие: Найдите диагональ прямоугольника со сторонами 5 и 12.
Интересный фактМашины и Механизмы. Машины и Механизмы, механические устройства, облегчающие труд и повышающие его производительность. Машины могут быть разной степени сложности – от простой одноколесной тачки до лифтов, автомобилей, печатных, текстильных, вычислительных машин. Энергетические машины преобразуют один вид энергии в другой. Например, генераторы гидроэлектростанции преобразуют механическую энергию падающей воды в электрическую энергию. Двигатель внутреннего сгорания преобразует химическую энергию бензина в тепловую, а затем в механическую энергию движения автомобиля. Зубчатая передача — это механизм или часть механизма, в состав которого входят зубчатые колёса..
При этом усилие от одного элемента к другому передаётся с помощью зубьев. Зубчатое колесо передачи с меньшим числом зубьев называется шестернёй, второе колесо с большим числом зубьев называется колесом. Пара зубчатых колёс имеющих одинаковое число зубьев в этом случае ведущее зубчатое колесо называется шестернёй, а ведомое — колесом.
Архимедов винт, винт Архимеда — механизм, исторически использовавшийся для передачи воды из низколежащих водоёмов в оросительные каналы. Он был одним из нескольких изобретений и открытий, традиционно приписываемых Архимеду, жившему в III веке до н. э. Архимедов винт стал прообразом шнека. Винт вращается обычно с помощью ветряного колеса либо вручную. В то время, как поворачивается нижний конец трубы, он собирает некоторый объём воды. Это количество воды будет скользить вверх по спиральной трубе во время вращения вала, пока наконец вода не выльется из вершины трубы, снабжая ирригационную систему.
Вопросы
Список использованных источников
Потурнак С.А. Кобычева Марина Викторовна
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: