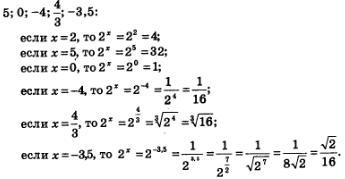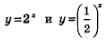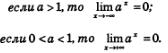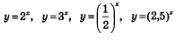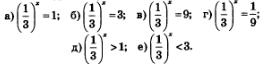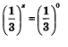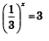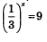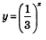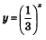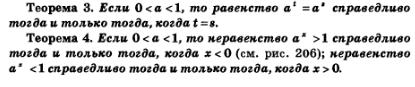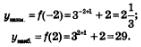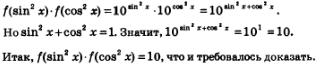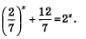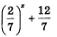|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Показательная функция, ее свойства и график
Показательная функция, ее свойства и график
Рассмотрим выражение 2х и найдем его значения при различных рациональных значениях переменной х, например, при х=2;
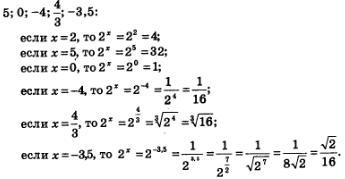
Вообще, какое бы рациональное значение мы ни придали переменной х, всегда можно вычислить соответствующее числовое значение выражения 2х. Таким образом, можно говорить о показательной функции у=2х, определенной на множестве Q рациональных чисел:
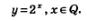
Рассмотрим некоторые свойства этой функции.
Свойство 1. 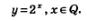 — возрастающая функция. Доказательство осуществим в два этапа. — возрастающая функция. Доказательство осуществим в два этапа.
Первый этап. Докажем, что если r — положительное рациональное число, то 2r >1.
Возможны два случая: 1) r — натуральное число, r = n; 2) 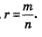 обыкновенная несократимая дробь, обыкновенная несократимая дробь, 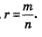

В левой части последнего неравенства имеем 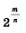 , а в правой 1. Значит, последнее неравенство можно переписать в виде , а в правой 1. Значит, последнее неравенство можно переписать в виде
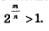
Итак, в любом случае выполняется неравенство 2г > 1, что и требовалось доказать.
Второй этап. Пусть x1 и x2 — рациональные числа, причем x1 и x2 < х2. Составим разность 2х2 -2х1 и выполним некоторые ее преобразования:
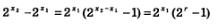
(мы обозначили разность х2 -х1 буквой r).
Так как r— положительное рациональное число, то по доказанному на первом этапе 2r > 1, т.е. 2r -1 >0. Число2х' также положительно, значит, положительным является и произведение 2x-1(2Г -1). Тем самым мы доказали, что справедливо неравенство 2Хг -2х' >0.
Итак, из неравенства х1< х2 следует, что 2х' <2x2, а это и означает, что функция у-2х — возрастающая.
Свойство 2. Функция 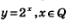 ограничена снизу и не ограничена сверху. ограничена снизу и не ограничена сверху.
Ограниченность функции снизу следует из неравенства 2х >0, справедливого для любых значений х из области определения функции. В то же время какое бы положительное число М ни взять, всегда можно подобрать такой показатель х, что будет выполняться неравенство 2х >М — что и характеризует неограниченность функции сверху. Приведем ряд примеров.

Свойство 3. Функция 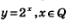 не имеет ни наименьшего, ни наибольшего значений. не имеет ни наименьшего, ни наибольшего значений.
То, что данная функция не имеет наибольшего значения, очевидно, поскольку она, как мы только что видели, не ограничена сверху. Но снизу она ограничена, почему же у нее нет наименьшего значения?
Предположим, что 2г — наименьшее значение функции (r — некоторый рациональный показатель). Возьмем рациональное число q <г. Тогда в силу возрастания функции у=2х будем иметь 2x <2г. А это значит, что 2r не может служить наименьшим значением функции.
Все это хорошо, скажете вы, но почему мы рассматриваем функцию у-2х только на множестве рациональных чисел, почему мы не рассматриваем ее, как другие известные функции на всей числовой прямой или на каком-либо сплошном промежутке числовой прямой? Что нам мешает? Обдумаем ситуацию.
Числовая прямая содержит не только рациональные, но и иррациональные числа. Для изученных ранее функций это нас не смущало. Например, значения функции у = х2 мы одинаково легко находили как при рациональных, так и при иррациональных значениях х: достаточно было заданное значение х возвести в квадрат.
А вот с функцией у=2x дело обстоит сложнее. Если аргументу х придать рациональное значение, то в принципе x вычислить можно (вернитесь еще раз к началу параграфа, где мы именно это и делали). А если аргументу х придать иррациональное значение? Как, например, вычислить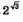 ? Этого мы пока не знаем. ? Этого мы пока не знаем.
Математики нашли выход из положения; вот как они рассуждали.
Известно, что 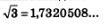 Рассмотрим последовательность рациональных чисел — десятичных приближений числа Рассмотрим последовательность рациональных чисел — десятичных приближений числа 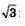 по недостатку: по недостатку:
1; 1,7; 1,73; 1,732; 1,7320; 1,73205; 1,732050; 1,7320508;... .
Ясно, что 1,732 = 1,7320, а 1,732050 = 1,73205. Во избежание подобных повторов отбросим те члены последовательности, которые заканчиваются цифрой 0.
Тогда получим возрастающую последовательность :
1; 1,7; 1,73; 1,732; 1,73205; 1,7320508;... .
Соответственно возрастает и последовательность
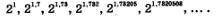
Все члены этой последовательности — положительные числа, меньшие, чем 22, т.е. эта последовательность — ограниченная. Апо теореме Вейерштрасса (см. § 30), если последовательность возрастает и ограничена, то она сходится. Кроме того, из § 30 нам известно, что если последовательность сходится, то только к одному пределу. Этот единственный предел договорились считать значением числового выражения 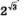 . И неважно, что найти даже приб-лиженное значение числового выражения 2 очень трудно; важно, что это — конкретное число (в конце концов, мы же не боялись говорить, что, например, . И неважно, что найти даже приб-лиженное значение числового выражения 2 очень трудно; важно, что это — конкретное число (в конце концов, мы же не боялись говорить, что, например, 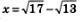 — корень рационального уравнения, — корень рационального уравнения, 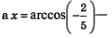 корень тригонометрического уравнения, не особенно задумываясь над тем, а что же это конкретно за числа: корень тригонометрического уравнения, не особенно задумываясь над тем, а что же это конкретно за числа: 
Итак, мы выяснили, какой смысл вкладывают математики в символ 2^. Аналогично можно определить, что такое 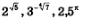 и вообще, что такое аa, где а — иррациональное число и а > 1. и вообще, что такое аa, где а — иррациональное число и а > 1.
А как быть в случае, когда 0 <а <1? Как вычислить, например, 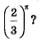 ? Самым естественным способом: считать, что ? Самым естественным способом: считать, что 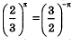 свести вычисления к случаю, когда основание степени больше 1. свести вычисления к случаю, когда основание степени больше 1.
Теперь мы можем говорить не только о степенях с произвольными рациональными показателями, но и о степенях с произвольными действительными показателями. Доказано, что степени с любыми действительными показателями обладают всеми привычными свойствами степеней: при умножении степеней с одинаковыми основаниями показатели складываются, при делении — вычитаются, при возведении степени в степень — перемножаются и т.д. Но самое главное, что теперь мы можем говорить о функции у-ах, определенной на множестве всех действительных чисел.
Вернемся к функции у = 2х, построим ее график. Для этого составим таблицу значений функции у=2x:

Отметим точки 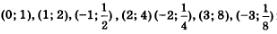 на координатной плоскости (рис. 194), они намечают некоторую линию, проведем ее (рис. 195). на координатной плоскости (рис. 194), они намечают некоторую линию, проведем ее (рис. 195).
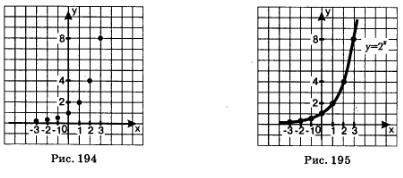
Свойства функции у - 2 х :
1) 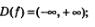
2) не является ни четной, ни нечетной; 248
3) возрастает;
4) не ограничена сверху, ограничена снизу;
5) не имеет ни наибольшего, ни наименьшего значений;
6) непрерывна;
7 ) 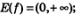
8) выпукла вниз.
Строгие доказательства перечисленных свойств функции у-2х приводят в курсе высшей математики. Часть этих свойств мы в той или иной мере обсудили ранее, часть из них наглядно демонстрирует построенный график (см. рис. 195). Например, отсутствие четности или нечетности функции геометрически связано с отсутствием симметрии графика соответственно относительно оси у или относительно начала координат.
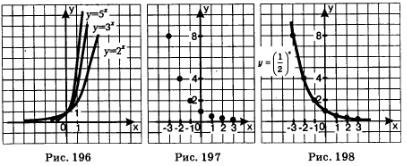
Аналогичными свойствами обладает любая функция вида у=ах, где а >1. На рис. 196 в одной системе координат построены, графики функций у=2х, у=3х, у=5х.
Рассмотрим теперь функцию 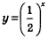 , составим для нее таблицу значений: , составим для нее таблицу значений:
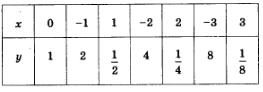
Отметим точки 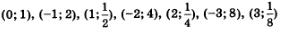 на координатной плоскости (рис. 197), они намечают некоторую линию, проведем ее (рис. 198). на координатной плоскости (рис. 197), они намечают некоторую линию, проведем ее (рис. 198).
Свойства функции 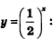
1 ) 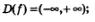
2) не является ни четной, ни нечетной;
3) убывает;
4) не ограничена сверху, ограничена снизу;
5) нет ни наибольшего, ни наименьшего значений;
6) непрерывна;
7) 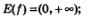
8) выпукла вниз.
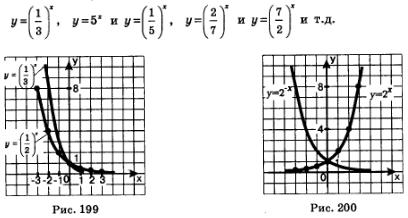
Аналогичными свойствами обладает любая функция вида у=ах, гдеО <а <1. На рис. 200 в одной системе координат построены графики функций 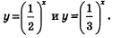
Обратите внимание: графики функций 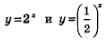 т.е. у=2х, симметричны относительно оси у (рис. 201). Это — следствие общего утверждения (см. § 13): графики функций у = f(х) и у = f(-х) симметричны относительно оси у. Аналогично будут симметричны относительно оси у графики функций у = 3х и т.е. у=2х, симметричны относительно оси у (рис. 201). Это — следствие общего утверждения (см. § 13): графики функций у = f(х) и у = f(-х) симметричны относительно оси у. Аналогично будут симметричны относительно оси у графики функций у = 3х и
Подводя итог сказанному, дадим определение показательной функции и выделим наиболее важные ее свойства.
Определение. Функцию вида 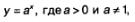 называют показательной функцией. называют показательной функцией.
Основные свойства показательной функции у =аx

График функции у=ах для а> 1 изображен на рис. 201, а для 0 <а < 1 — на рис. 202.
Кривую, изображенную на рис. 201 или 202, называют экспонентой. На самом деле математики экспонентой обычно .называют саму показательную функцию у=ах. Так что термин "экспонента" используется в двух смыслах: и для наименования показательной функции, и для названия графика показательной функции. Обычно по смыслу бывает ясно, идет речь о показательной функции или о ее графике.
Обратите внимание на геометрическую особенность графика показательной функции у=ах: ось х является горизонтальной асимптотой графика. Правда, обычно это утверждение уточняют следующим образом.
Ось х является горизонтальной асимптотой графика функции
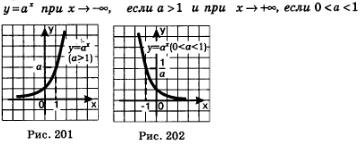
Иными словами
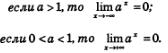
Первое важное замечание. Школьники часто путают термины: степенная функция, показательная функция. Сравните:
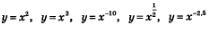
— это примеры степенных функций;
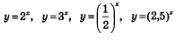
— это примеры показательных функций.
Вообще, у = хг, где г — конкретное число, — степенная функция (аргумент х содержится в основании степени);
у = а", где а — конкретное число (положительное и отличное от 1), — показательная функция (аргумент х содержится в показателе степени).
Атакую «экзотическую» функцию, как у = х", не считают ни показательной, ни степенной (ее иногда называют показательно-степенной).
Второе важное замечание. Обычно не рассматривают показательную функцию с основанием а = 1 или с основанием а, удовлетворяющим неравенству а <0 (вы, конечно, помните, что выше, в определении показательной функции, оговорены условия: а >0и а Дело в том, что если а = 1, то для любого значения х выполняется равенство Iх = 1. Таким образом, показательная функция у = а" при а = 1 «вырождается» в постоянную функцию у = 1 — это неинтересно. Если а = 0, то 0х = 0 для любого положительного значения х, т.е. мы получаем функцию у = 0, определенную при х >0, — это тоже неинтересно. Если, наконец, а <0, то выражение а" имеет смысл лишь при целых значениях х, а мы все-таки предпочитаем рассматривать функции, определенные на сплошных промежутках.
Прежде чем переходить к решению примеров, заметим, что показательная функция существенно отличается от всех функций, которые вы изучали до сих пор. Чтобы основательно изучить новый объект, надо рассмотреть его с разных сторон, в разных ситуациях, поэтому примеров будет много.
Пример 1. Решить уравнения и неравенства:
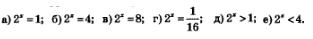
Решение, а) Построив в одной системе координат графики функций у = 2х и у = 1, замечаем (рис. 203), что они имеют одну общую точку (0; 1). Значит, уравнение 2х = 1 имеет единственный корень х =0.
Итак, из уравнения 2х =2° мы получили х=0.
б) Построив в одной системе координат графики функций у = 2х и у=4, замечаем (рис. 203), что они имеют одну общую точку (2; 4). Значит, уравнение 2х =4 имеет единственный корень х=2.
Итак, из уравнения 2х =22 мы получили х=2.
в) и г) Исходя из тех же соображений, делаем вывод, что уравнение 2х =8 имеет единственный корень, причем для его отыскания графики соответствующих функций можно и не строить;
ясно, что х=3, поскольку 23 =8. Аналогично находим единственный корень уравнения
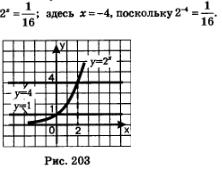
Итак, из уравнения 2х = 23 мы получили х = 3, а из уравнения 2х = 2x мы получили х = -4.
д) График функции у = 2х расположен выше графика функции у = 1 при x >0 — это хорошо читается по рис. 203. Значит, решением неравенства 2х > 1 служит промежуток 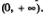
е) График функции у = 2x расположен ниже графика функции у = 4 при х<2 — это хорошо читается по рис. 203. Значит, решением неравенства 2х <4служит промежуток 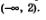
Вы заметили, наверное, что в основе всех выводов, сделанных при решении примера 1, лежало свойство монотонности (возрастания) функции у=2х. Аналогичные рассуждения позволяют убедиться в справедливости следующих двух теорем.
[[Image:M1047.jpg|480px|Теорема
Пример 2. Решить уравнения и неравенства:
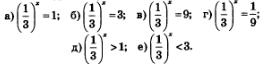
Решение, а) Построив в одной системе координат графики функций 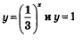 , замечаем (рис. 205), что они имеют одну общую точку (0; 1). , замечаем (рис. 205), что они имеют одну общую точку (0; 1).
Значит, уравнение 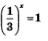 имеет единственный корень х = 0. имеет единственный корень х = 0.

Итак, из уравнения 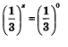 мы получили х = 0. мы получили х = 0.
б) Построив в одной системе координат графики функций 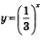 у = 3, замечаем (см. рис. 205), что они имеют одну общую точку (-1; 3). Значит, уравнение у = 3, замечаем (см. рис. 205), что они имеют одну общую точку (-1; 3). Значит, уравнение 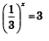 имеет единственный корень х = -1. имеет единственный корень х = -1.
Итак, из уравнения  мы получили х = -1. мы получили х = -1.
в) и г) Исходя из тех же соображений, делаем вывод, что уравнение 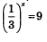 имеет единственный корень, причем для его отыскания графики соответствующих функций можно и не строить; ясно, что х = - 2, поскольку имеет единственный корень, причем для его отыскания графики соответствующих функций можно и не строить; ясно, что х = - 2, поскольку 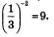 . Аналогично находим единственный корень уравнения . Аналогично находим единственный корень уравнения 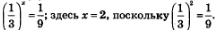
Итак, из уравнения 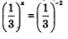 мы получили х =- 2, а из уравнения мы получили х =- 2, а из уравнения 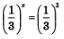 мы получили х = 2 мы получили х = 2
д) График функции 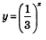 расположен выше графика функции у = 1 при x <0 — это хорошо читается по рис. 205. Значит, решением неравенства расположен выше графика функции у = 1 при x <0 — это хорошо читается по рис. 205. Значит, решением неравенства 
е) График функции 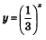 расположен ниже графика функции у = 3 при х > —1 — это хорошо читается по рис. 205. Значит, решением неравенства расположен ниже графика функции у = 3 при х > —1 — это хорошо читается по рис. 205. Значит, решением неравенства 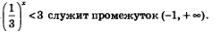
В основе всех выводов, сделанных при решении примера 2, лежало свойство монотонности (убывания) функции 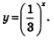 . Аналогичные рассуждения позволяют убедиться в справедливости следующих двух теорем. . Аналогичные рассуждения позволяют убедиться в справедливости следующих двух теорем.
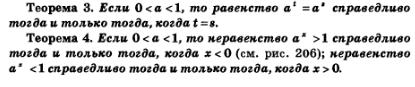
Пример 3. Построить график функции у = 3-3x +2 и найти наибольшее и наименьшее значения этой функции на отрезке [-2, 2].
Решение. Можно действовать так: построить график функции у-3х, затем осуществить его растяжение от оси х с коэффициентом 3, а затем полученный график поднять вверх на 2 единицы масштаба. Но удобнее воспользоваться тем, что 3- 3* =3*+1, и, следовательно, строить график функции у=Зх*1 + 2.
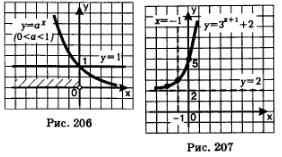
Перейдем, как неоднократно уже делали в таких случаях, к вспомогательной системе координат с началом в точке (-1; 2) — пунктирные прямые х = - 1 и 1x = 2 на рис. 207. «Привяжем» функцию у=3* к новой системе координат. Для этого выберем контрольные точки для функции 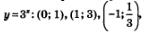 , но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 207). Затем по точкам построим экспоненту — это и будет требуемый график (см. рис. 207). , но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 207). Затем по точкам построим экспоненту — это и будет требуемый график (см. рис. 207).
Чтобы найти наибольшее и наименьшее значения заданной функции на отрезке [-2, 2], воспользуемся тем, что заданная функция возрастает, а потому свои наименьшее и наибольшее значения она принимает соответственно в левом и правом концах отрезка.
Итак:
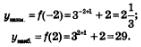
Пример 4. Решить уравнение и неравенства:
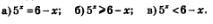
Решение, а) Построим в одной системе координат графики функций у=5* и у=6-х (рис. 208). Они пересекаются в одной точке; судя по чертежу, это — точка (1; 5). Проверка показывает, что на самом деле точка (1; 5) удовлетворяет и уравнению у = 5*, и уравнению у=6-х. Абсцисса этой точки служит единственным корнем заданного уравнения.
Итак, уравнение 5х = 6- х имеет единственный корень х = 1.
б) и в) Экспонента у- 5х лежит выше прямой у=6-х, если х>1, — это хорошо видно на рис. 208. Значит, решение неравенства5*>6-х можно записать так: х>1. А решение неравенства 5х <6 - х можно записать так: х < 1.
Ответ: а)х = 1; б)х>1; в)х<1.
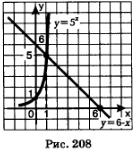
Пример 5. Дана функция 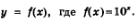 Доказать, что Доказать, что 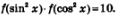
Решение. По условию 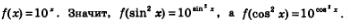 Имеем: Имеем:
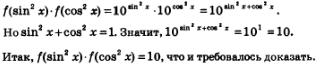
Пример 6. Решить уравнение: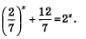
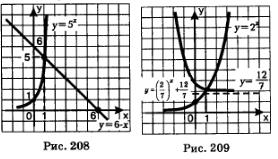
Решение. Положим 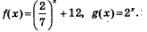 Заметим, что функция у = f(х)убывает, а функция у =g(х) возрастает. Воспользуемся известным фактом: если функция у = f(х)убывает, а функция у = g(х)возрастает, и если уравнение f()=g(x) имеет корень, то только один. Нетрудно догадаться, что заданное уравнение имеет корень х = 1: подставив значение х = 1 в заданное уравнение, получим Заметим, что функция у = f(х)убывает, а функция у =g(х) возрастает. Воспользуемся известным фактом: если функция у = f(х)убывает, а функция у = g(х)возрастает, и если уравнение f()=g(x) имеет корень, то только один. Нетрудно догадаться, что заданное уравнение имеет корень х = 1: подставив значение х = 1 в заданное уравнение, получим 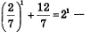 верное числовое равенство. верное числовое равенство.
Так как функция 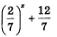 убывает, а функция у = 2x возрастает, то корень у заданного уравнения только один, и этим корнем является найденное выше значение х = 1 (рис. 209). убывает, а функция у = 2x возрастает, то корень у заданного уравнения только один, и этим корнем является найденное выше значение х = 1 (рис. 209).
Ответ: x = 1.
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|