|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Построение треугольника с данными сторонами. Полные уроки ТЕМА УРОКА: Построение треугольника с данными сторонами.
Цели урока:
|
| Файл:19022011 10.gif |
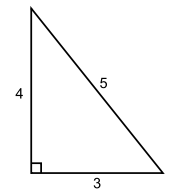
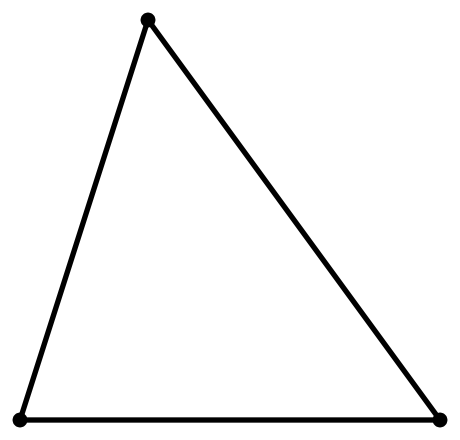
Дано: отрезки a,b,c. Построить: ΔABC, так чтобы AB=a, BC=b, CA=c |
| Файл:19022011 11.gif |
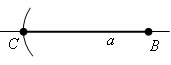
Построение: На луче откладываем отрезок AC=а. |
| Файл:19022011 12.gif |
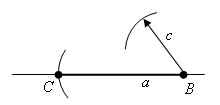
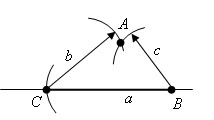
Строим окружность (А,а) и окружность (С,b), B = пересечение двух окружностей ΔABC - есть искомый треугольник. |
Хочу обратить ваше внимание на обозначение окружностей (А,а) и(С,b).
Что подразумевает собой данное обозначение?
Для большего удобства и краткости записи многие учебники, а также люди какие часто сталкиваются с построением фигур используют компактный вариант записи который в некотором смысле является даже более наглядным. В нашем же случаи это означает что мы строим окружность с центром в точке "А" и радиусом равным отрезку "а" и с центром в точке "С" и радиусом равным отрезку "b".
Так же обратите внимание на последний рисунок наши две окружности пересекаются в двух точка одну мы назвали "В", а вторая осталась не обозначенной, как Вы уже догадались если соединить эту точку с основанием, у нас получатся два треугольники, какие будут абсолютно идентичными но зеркально отражены по оси ОХ.
Интересный факт:
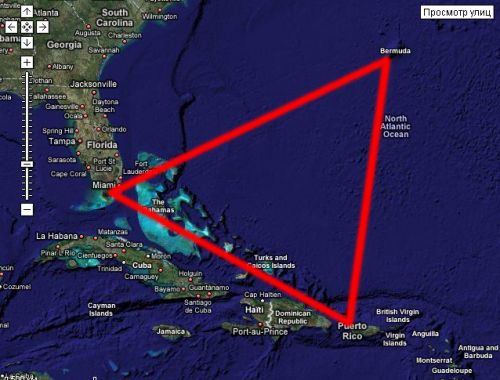
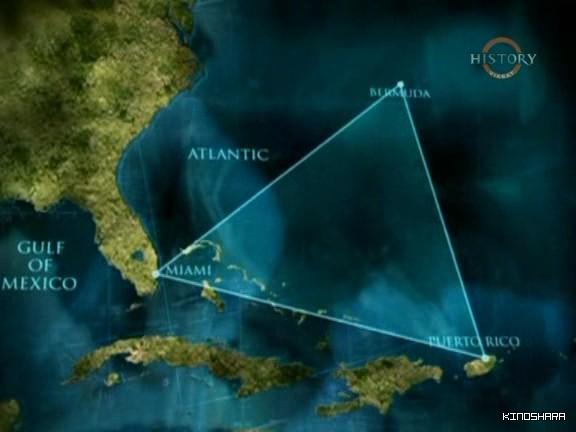
Бермудский треугольник.
Мистика или рутина?
Разумеется, вкупе с рядом других сообщений о гибели самолетов (например, ВВС США, в 1945 году потеряли пять машин) две катастрофы привели к появлению самых разнообразных версий. Вплоть до откровенной фантастики: космические корабли пришельцев, возникающие из-за особых погодных условий в атмосфере лазерные лучи и порталы в другие миры. Версия BBC скромнее и вместе с тем убедительнее.
По мнению привлеченных агентством авиационных экспертов, основной проблемой стала крайне ненадежная конструкция самолета. «Авро Тюдоры» могли подниматься на высоту свыше 9 тыс. метров, но на такой высоте требуется включать специальные обогреватели: мороз минус 40 градусов по Цельсию грозил не только неудобствами для пассажиров. Пилот «Звездного тигра», столкнувшись с отказом обогревателя, был вынужден снизить высоту полета вплоть до 600 м, что и повлекло за собой сразу две другие проблемы.
Во-первых, самолеты неспроста летают на большой высоте: там ниже сопротивление воздуха и, следовательно, расход топлива. Вблизи поверхности теплее, но расход топлива резко возрастает: «Тигр» мог попросту не дотянуть до аэродрома, особенно если учесть то, что он сбился с курса, столкнулся с неожиданно сильным встречным ветром и в итоге задерживался минимум на час.
Вторая проблема, связанная с низкой высотой, – это то, что если лайнер начнет неожиданно падать, то на выправление его курса времени у пилотов остается намного меньше. «С такой высоты вы можете за несколько секунд свалиться в море», – утверждает Эрик Ньютон, приглашенный специалист по расследованию авиакатастроф. Добавьте к малому запасу времени малый запас топлива – и для исчезновения самолета уже не потребуется ссылок на инопланетян или иные мистические причины.
Впрочем, низкой высотой полета и сопряженными с этим проблемами выводы BBC не ограничиваются. Авторам расследования удалось выяснить, что к Азорским островам «Тигр» уже прилетел не только с забарахлившим обогревателем, но и с одним отказавшим компасом. Голден Стор, бывший пилот и руководитель полетов той самой авиакомпании BSAA, поделился воспоминаниями о том, как были устроены «Авро Тюдоры» изнутри. По словам летчика, под полом кабины была жуткая путаница: трубопроводы гидравлической системы, при помощи которой осуществляется управление лайнером, соседствовали с системой кондиционирования воздуха и обогревателем.
Обогреватель – тот самый, вышедший из строя – работал на авиационном топливе и представлял собой раскаленную трубу в опасном соседстве с жизненно важной системой управления. Если бы гидравлическая система дала течь, то использовавшаяся в ней жидкость вкупе с парами топлива могла способствовать взрыву и пожару, который без системы автоматического тушения привел бы к быстрой гибели лайнера. «В этом отсеке даже не было сигнализации, – рассказал Стор. – Поэтому о пожаре бы так и не узнали».
Вопросы:
- Что такое треугольник?
- Чему равна сумма углов треугольника?
- Какие виды треугольников существуют?
- Без каких инструментов не не возможно построить треугольник с данными сторонами?
- Для чего нам нужна окружность при построении?
Список использованных источников:
- Дм. Ефремов, Новая геометрия треугольника
- Урок на тему "Построение геометрических фигур" Автор: Марина Александровна, г. Киев.
- Понарин Я.П. Элементарная геометрия
- Стадник Л.Г. Геометрия. 7 класс. Комплексная зачетная тетрадь.
- Уроки геометрии Кирилла и Мефодия. 7 класс (2005)
Над уроком работали:
Марина Александровна
Постурнак С.А.
Обух Г.Н.
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: