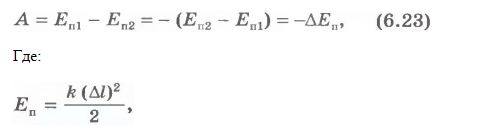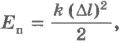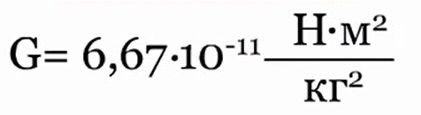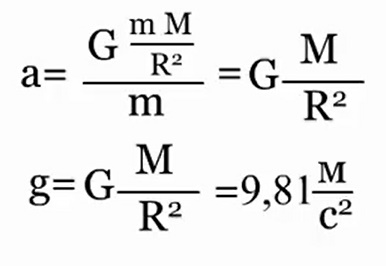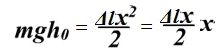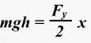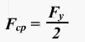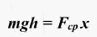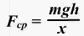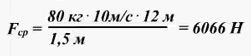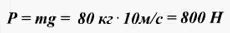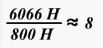|
Гипермаркет знаний>>Физика и астрономия>>Физика 10 класс>>Физика: Потенциальная энергия
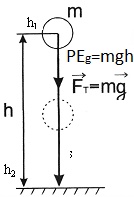
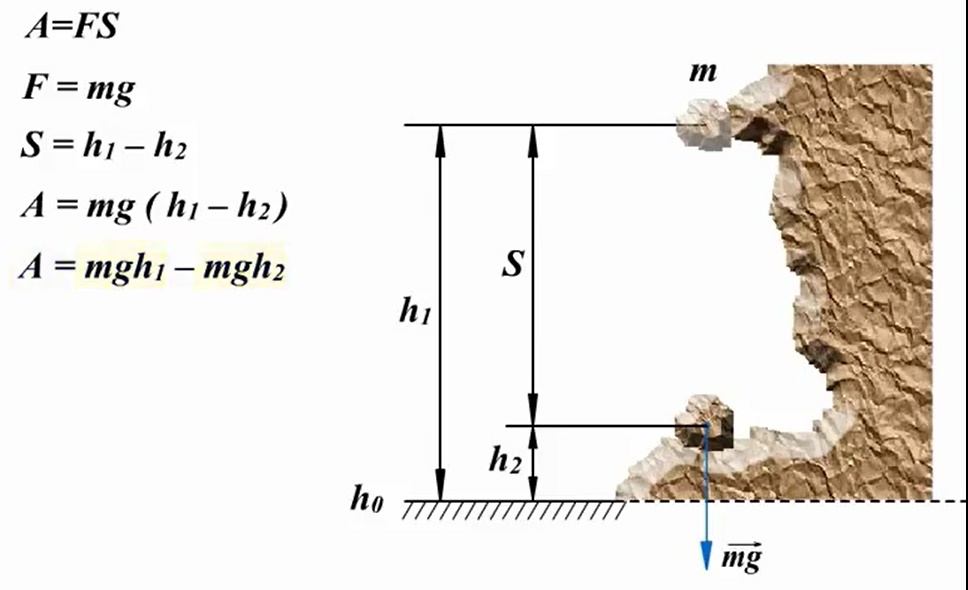
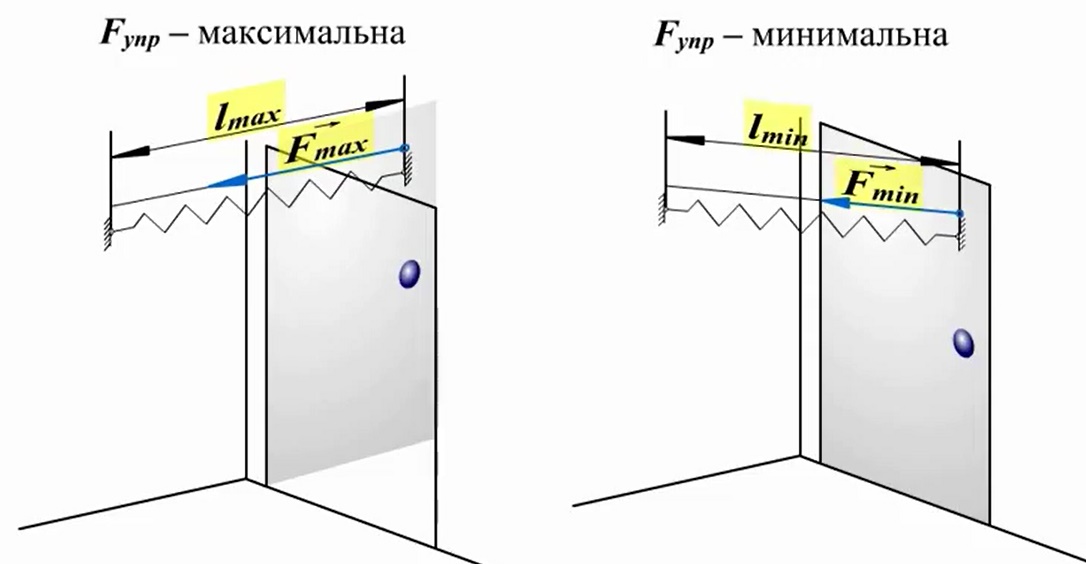
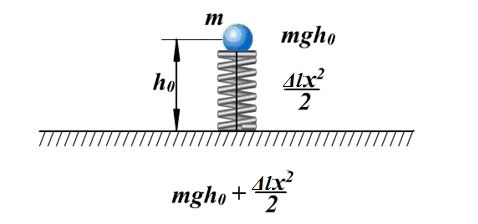
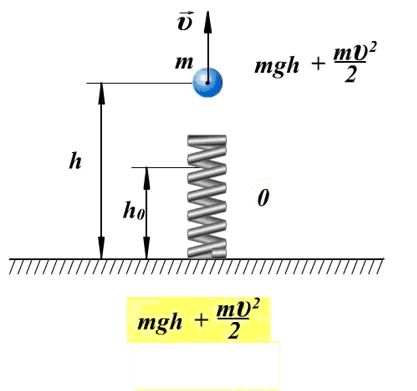
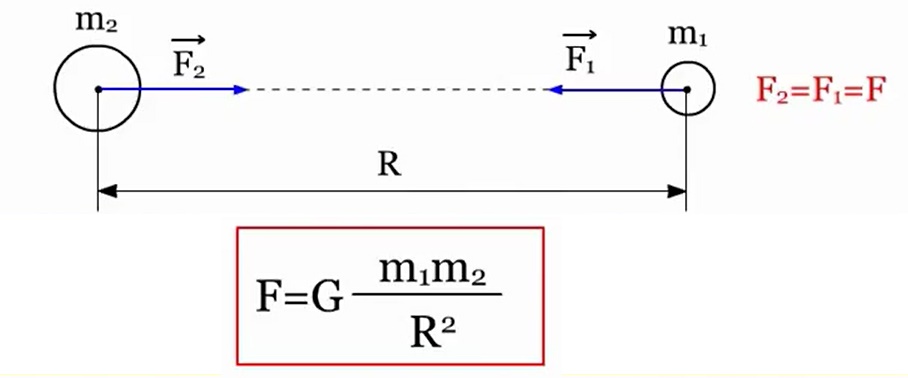
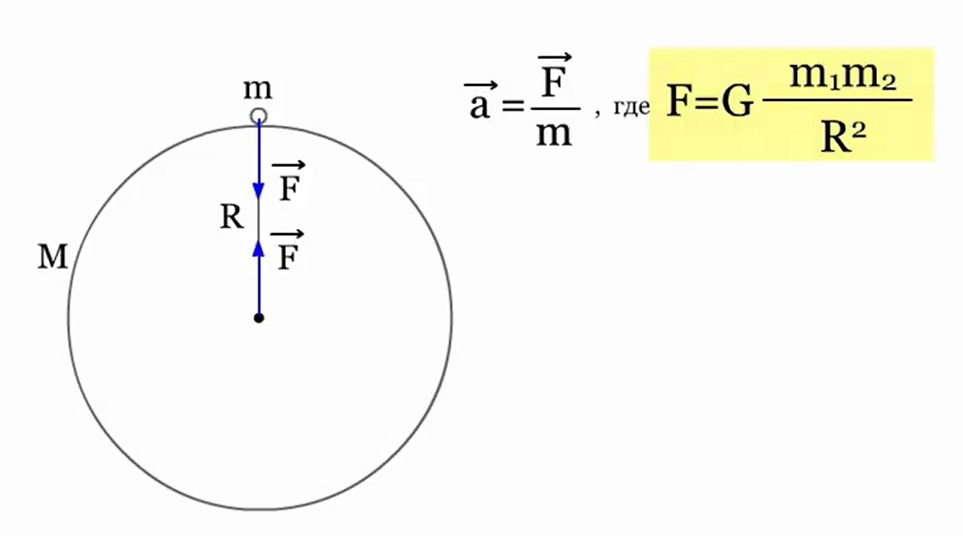
Потенциальная энергия Что нам известно о потенциальной энергии гравитации? Представим поверхность Земли. Мы можем быть, где угодно, где есть гравитация, тогда потенциальная энергия появится из гравитационного поля данной нам массы. Мы знаем, что если есть некоторое тело массой m, расположенное на высоте h в гравитационном поле с ускорением свободного падения g, или 9,8 м/с^2. То потенциальная энергия гравитации этого тела в этой точке равняется произведению массы, ускорения свободного падения и высоты. Данное определение можно рассматривать как величину силы гравитации. А чему же равна потенциальная энергия? Если объект обладает потенциальной энергией, и ничто не останавливает его движения, то он полетит вниз с ускорением и большая часть потенциальной энергии, а по сути, вся она, перейдет в кинетическую энергию. Так что другими словами, потенциальная энергия является энергией, которая «запасена» в объекте, или той энергией, которой объект обладает в соответствии с его нахождением. Затем чтоб тело или объект имели эту энергию, она должна откуда-то появиться, как в случае с потенциальной энергией гравитации. Можно рассматривать потенциальную энергию гравитации как работу, нужную для передвижения объекта в указанное положение. Исследуем движение тела под действием силы тяжести. Предположим, что обломок скалы массой m падает с высоты h1 относительно подножия горы и останавливается на уступе на высоте h2. При таких условиях работу выполняет сила тяжести: A=FS. Поскольку сила тяжести равна F=gm, а перемещение равно S=h1 – h2, то работа будет равняться A=mg(h1 – h2) или A=mgh1 – mgh2. Величина mgh характеризует состояние тела в поле земного тяготения и называется потенциальной энергией. С учетом этого формулу для работы силы тяжести можно представить так: Как видим, что работа силы тяжести - это изменение потенциальной энергии тела с противоположным знаком. В нашем примере сила тяжести совершила положительную работу, а изменение потенциальной энергии отрицательно, т.е. потенциальная энергия уменьшилась. Потенциальной энергией могут так же обладать упругодеформированные тела. Если открыть подпружиненную дверь, то возникшая наряду с этим сила упругости способна совершить работу, закрывая дверь следом. Однако этот случай является особым, поскольку работа будет совершена переменной по модулю силой. Но потому как в этой ситуации работа выполняется за счет запаса энергии, можно утверждать, работа силы упругости равняется разности потенциальных энергий: В этой формуле k – это жесткость; Δl – величина деформации. Подведя итог всему выше упомянутому, приходим к заключению, что во всех случаях работа силы обусловливает изменение энергии тела, от сюда следует, что работа есть мера изменения энергии. Формулы работы для силы тяжести и силы упругости выглядят так: Закон сохранения энергииОчевидно, что при взаимодействии тела могут обмениваться энергий, например движущийся бильярдный шаг при столкновении с подобным неподвижным шаром передает ему свою кинетическую энергию. Если при этом первый шар остановится, то он отдаст второму всю свою кинетическую энергию. Рассмотрим пример с потенциальной энергией. Шарик массой m расположен на сжатой пружине, пружина связана нитью. Шарик обладает потенциальной энергией касательно поверхности стола. Потенциальная энергия сжатой пружины - Если пережечь нить, шарик начнет двигаться вверх, и в некоторый момент будет иметь скорость ύ на высоте h, в тоже время энергия пружины равна 0, а полная энергия системы будет равна: Интересные факты:Исааку Ньютону принадлежит открытие закона всемирного тяготения. Вот его формулировка: какие-либо два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними: Коэффициентом пропорциональности в данном законе является одна из фундаментальных физических постоянных – гравитационная постоянная. Закон сформулирован для точечных тел, т.е. для материальных точек, однако он справедлив и для больших однородных шаров, например, планет. В этом случае полагают, что масса таких тел сосредоточена в центре и расстояние R берут между центрами. Сила тяжесть есть частный случай проявления закона всемирного тяготения. Тело массой m, притягивается Землей массой M, расстояние между их центрами равно Земному радиусу R. В соответствии со вторым законом Ньютона тело получает ускорение, где F – сила гравитационного притяжения. Следовательно, ускорение тела а и является ускорением свободного падения g, которое равное для всех тел и равное вблизи поверхности Земли. Сила, извещающая телу это ускорение и является силой тяжести: F=mg. Из формулы очевидно, что сила тяжести прямо пропорциональна массе тела. ЗадачаКаскадер, масса которого 80 кг прыгнул с высоты 12 м на растянутую страховочную сетку. В следствии она прогнулась на 1,5 м. Найдите среднюю силу, с которой каскадер давит на сетку? Решение: используя закон сохранения энергии можно сделать запись: То есть потенциальная энергия каскадера на высоте h равна потенциальной энергии упругодеформированной сетки. Сила давления на сетку по модулю равна возникающей в ней силе упругости: Fy= Δlx. Подставим в закон сохранения энергии: Поскольку сила упругости линейно зависит от деформации сетки, то средняя сила давления будет равна половине максимальной силы упругости Тогда закон сохранения энергии принимает вид: Выразим из формулы среднюю силу: Произведем расчеты: Соответственно, каскадер давит на сетку со средней силой равной примерно 6 кН.
Примечание: учитывая, что нормальный вес этого человека составляет Подумайте и ответьте на вопросы: 1. Подумайте, в чем же состоит сходство кинетической энергии тела и потенциальной? |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: