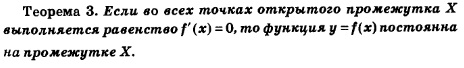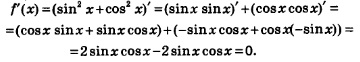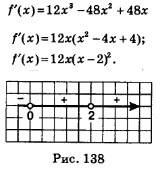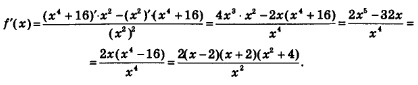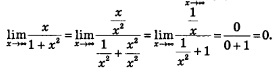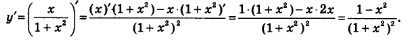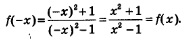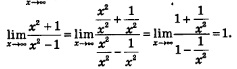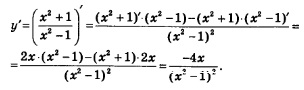|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Применение производной для исследования функций на монотонность и экстремумы
§ 35. Применение производной для исследования функций на монотонность и экстремумы
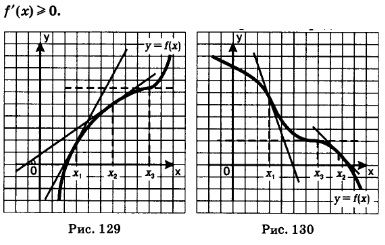
На рис. 130 представлен график некоторой убывающей дифференцируемой функции у = f(х). Проведем касательные к графику в точках х= х1 и х= х2. У построенных прямых? Общее то, что обе они составляют с осью х тупой угол, а значит, у обеих прямых отрицательный угловой коэффициент. Но угловой коэффициент касательной равен значению производной в абсциссе точки касания. Таким образом, если функция возрастает на промежутке и имеет на нем производную, то производная неотрицательна; если функция убывает на промежутке и имеет на нем производную, то производная неположительна. Доказательства этих теорем проводят обычно в курсе высшей математики. Мы ограничимся проведенными выше рассуждениями «на пальцах» и для вящей убедительности дадим еще физическое истолкование сформулированных теорем. Пусть по прямой движется материальная точка, s =s(t) — закон движения. Если скорость все время положительна, то точка постоянно удаляется от начала отсчета, т.е. функция s = s(t) возрастает. Если же скорость все время отрицательна, то точка постоянно приближается к началу отсчета, т.е. функция s = s(t) убывает. Если скорость движения была положительна, затем в какой-то отдельный момент времени обратилась в нуль, а потом снова стала положительной, то движущееся тело в указанный момент времени как бы притормаживает, но все равно продолжает удаляться от начальной точки. Так что и в этом случае функция s = s(t) возрастает. А что такое скорость? Это производная пути по времени. Значит, от знака производной (скорости) зависит характер монотонности функции — в данном случае функции s = s(t). Об этом как раз и говорят обе сформулированные теоремы. Пример 1. Доказать, что функция
Пример 2. а) Доказать, что функция у = 5соз х + зт4х - 10х убывает на всей числовой прямой; Решение, а) Найдем производную заданной функции:
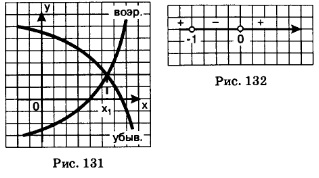
б) Рассмотрим уравнение 5соз х + sin4х - 10х = х3 + 5. Как было установлено только что, у = 5соsх + sin4х-10х — убывающая функция. В то же время у = х3 +5 — возрастающая функция. Имеет место следующее утверждение: если одна из функций у = f(х) или у = s(х) возрастает, а другая убывает и если уравнение f(х) = g(х) имеет корень, то только один (рис. 131 наглядно иллюстрирует это утверждение). Корень заданного уравнения подобрать нетрудно — это число х= 0 (при этом значении уравнение обращается в верное числовое равенство 5 = 5). Пример 3. а) Исследовать на монотонность функцию у = 2х3 + Зх2 -1; б) построить график этой функции. Решение, а) Исследовать функцию на монотонность — это значит выяснить, на каких промежутках области определения функция возрастает, а на каких убывает. Согласно теоремам 1 и 2 это связано со знаком производной. Найдем производную данной функции: f'(х)=6х2+6х и далее f'(х)=6x(х + 1). На рис. 132 схематически указаны знаки производной по промежуткам области определения: на луче (-оо,-1) производная положительна, на интервале (-1,0) — отрицательна, на луче (0,+ — положительна. Значит, на первом из указанных промежутков функция возрастает, на втором убывает, на третьем возрастает.
Таким образом, заданная функция возрастает на луче б) Графики функций строят «по точкам». Для этого надо составить таблицу значений функции у= 2х3 +3х2 -1, куда обязательно следует включить значения функции в концевых точках промежутков монотонности х = -1 и х = 0 и еще пару-тройку значений:
Завершая рассуждения по исследованию функций на монотонность, обратим внимание на одно обстоятельство. Мы видели, что если на промежутке X выполняется неравенство f'(x) >0, то функция у-f(х) возрастает на промежутке X; если же на промежутке X выполняется неравенство f'(x) < 0, то функция убывает на этом промежутке. А что будет, если на всем промежутке выполняется тождество (х) =0 ? Видимо, функция не должна ни возрастать, ни убывать. Что же это за функция? Ответ очевиден — это постоянная функция у = С (буква С — первая буква слова соп81ап1а, что означает «постоянная»). Справедлива следующая теорема, формальное доказательство которой мы не приводим, ограничиваясь приведенными выше правдоподобными рассуждениями. В дальнейшем эта теорема будет нами востребована, т.е. в ее пользе для математики мы сумеем убедиться. А сейчас приведем (для наиболее любознательных) пример использования теоремы 3 (из разряда математических развлечений). Мы приведем новый способ доказательства хорошо вам известного тождества sin2x + cos2 x= 1.
Таким образом, С = 1, т. е. sin2 х+соs2 х = 1
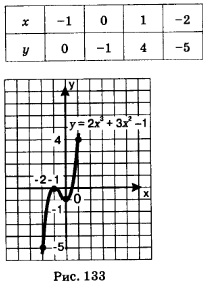
Вернемсяк графику функции у=2 х3 +3х2 -1(рис. 133). На графике есть две уникальные точки, определяющие его структуру, — это точки (-1; 0) и (0; -1). В этих точках: 1) происходит изменение характера монотонности функции (слева от точки х = -1 функция возрастает, справа от нее, но только до точки х =0, функция убывает; слева от точки х =0 функция убывает, справа от нее возрастает); 2) касательная к графику функции параллельна оси х, т.е. производная функции в каждой из указанных точек равна нулю; 3) f(-1) — наибольшее значение функции, но не во всей области определения, а в локальном смысле, т.е. по сравнению со значениями функции из некоторой окрестности точки х = -1. Точно так же f(0) — наименьшее значение функции, но не во всей области определения, а в локальном смысле, т.е. по сравнению со значениями функции из некоторой окрестности точки х = 0. А теперь взгляните на рис. 134, где изображен график другой функции. Не правда ли, он похож на предыдущий график? На нем те же две уникальные точки, но одна из указанных выше трех особенностей этих точек изменилась: теперь касательные к графику в этих точках не параллельны оси х. В точке х = -1 касательная вообще не существует, а в точке х = 0 она перпендикулярна оси х (точнее, она совпадает с осью у).
Определение 1. Точку х =х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой (кроме самой точки х =х0) выполняется неравенство: Так, функции, графики которых изображены на рис. 133 и 134, имеют точку минимума х=0. Почему? Потому что у этой точки существует окрестность, например,
Так, функции, графики которых изображены на рис. 133 и 134, имеют точку максимума х= — 1. Почему? Потому что у этой точки Точки минимума и максимума функции объединяют общим термином — точки экстремума (от латинского слова ехtremum — «крайний»). Как искать точки экстремума функции? Ответ на этот вопрос мы сможем найти, еще раз проанализировав графические модели, представленные на рис. 133 и 134. Обратите внимание: для функции, график которой изображен на рис. 133, в обеих точках экстремума производная обращается в нуль (касательные параллельны оси х). А для функции, график которой изображен на рис. 134, в обеих точках экстремума производная не существует. Это не случайно, поскольку, как доказано в курсе математического анализа, справедлива следующая теорема.
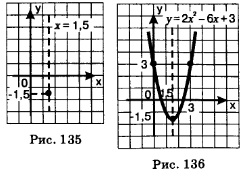
Приравняв производную нулю, получим: 4х-6=0; х = 1,5. Подставив найденное значение х в уравнение параболы, получим: у = 21,52 - 6-1,5 + 3 = -1,5. Итак, вершиной вдраболы служитточка(1,5; -1,5), а осью параболы — прямая х=1,5 (рис. 135). В качестве контрольных точек удобно взять точку (0; 3) и симметричную ей относительно оси параболы точку (3; 3). На рис. 136 по найденным трем точкам построена парабола — график заданной квадратичной функции.
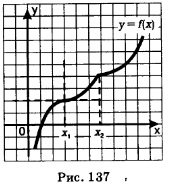
А теперь вернемся к теореме 4, которая говорит, что если в точке х = х0 функция у = f(х) имеет экстремум, то х = х0 — стационарная или критическая точка функции. Возникает естественный вопрос: верна ли обратная теорема, т.е. верно ли, что если х = х0 — стационарная или критическая точка, то в этой точке функция имеет экстремум? Отвечаем: нет, неверно. Посмотрите на рис. 137, где изображен график возрастающей функции, не имеющей точек экстремума. У этой функции есть стационарная точка х = х1,в которой производная обращается в нуль (в этой точке график функции имеет касательную, параллельную оси х), но это не точка экстремума, а точка перегиба, и есть критическая точка х =х2, в которой производная не существует, но это также не точка экстремума, а точка излома графика. Поэтому скажем так: теорема 4 дает только необходимое условие экстремума (справедлива прямая теорема), но оно не является достаточным условием (обратная теорема не выполняется).
Если же и слева, и справа от стационарной или критической точки производная имеет один и тот же знак, то в этой точке экстремума нет, именно так обстоит дело с функцией, график которой изображен на рис. 137.
Тогда: а) если у этой точки существует такая окрестность, что в ней при х<х0 выполняется неравенство f(x) < 0,а при x > x0 — неравенство f"x)>0, то x =x0 — точка минимума функции У=f(х); б) если у этой точки существует такая окрестность, что в ней при x < x0 выполняется неравенство f"(x) > О, а при x > x0 — неравенство f(х) < О, то x = x0 — точка максимума функции У=f(х); в) если у этой точки существует такая окрестность, что в ней и слева, и справа от точки x0 знаки производной одинаковы, то в точке x = x0 экстремума нет.
Решение, а) Найдем производную данной функции: Производная обращается в нуль в точках х = О и х = 2 — это две стационарные точки заданной функции. На рис. 138 схематически указаны знаки производной по промежуткам области определения: на промежутке В точке минимума х = 0 имеем f(0) = —11 (подставили значение х = 0 в аналитическое задание функции), значит, б) Чтобы построить график функции, нужно знать особо важные точки графика. К таковым относятся: — стационарная точка х = 2; в этой точке — точки пересечения с осями координат; в данном примере это уже найденная точка (0; -11) — точка пересечения графика с осью у. И еще: можно догадаться, что f(1)=0, значит, найдена точка пересечения графика с осью х — это точка (1; 0). Итак, мы имеем точку минимума (0; -11), точку пересечения графика с осью х — точку (1; 0) и стационарную точку (2; 5). В этой точке касательная к графику функции горизонтальна, но это не точка экстремума, а точка перегиба.
Завершая этот пункт, заметим, что мы фактически выработали
1. Найти производную f'(х).
4) Делаем выводы: на луче(-°°, -2] функция убывает, на полуинтервале [-2, 0) функция возрастает, на полуинтервале (0, 2] функция убывает, на луче [2, + функция возрастает. Далее, х = -2 — точка минимума, причем
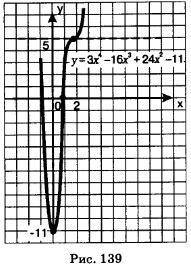
За годы изучения курса алгебры в школе вы накопили достаточно большой опыт построения графиков функций. В основном вы строили графики «по точкам», т.е. для заданной функции у = f(х) находили контрольные точки Графики любых функций строят по точкам. Но в тех случаях, когда вид графика заранее неизвестен, эти точки надо выбирать со смыслом — уметь выделять особо важные точки графика, которые определяют его структуру. Об этом мы уже говорили выше, когда строили графики функций у=2х3 +3х2 -1 (см. рис. 133) и у=Зх4 -16х3 +24х2 -11(см. рис. 139). К особо важным точкам графика функции у = f(х) относят: — стационарные и критические точки; В тех случаях, когда речь идет о построении графика незнакомой функции, когда заранее невозможно представить вид графика, полезно применять определенную схему исследования свойств функции, которая помогает составить представление о ее графике. Когда такое представление составится, можно приступить к построению графика по точкам. В курсе математического анализа разработана универсальная схема исследования свойств функции и построения графика функции, позволяющая строить весьма сложные графики. Для наших нужд будут достаточны упрощенные варианты указанной схемы. 1) Если функция у = f(х) непрерывна на всей числовой прямой, то достаточно найти стационарные и критические точки, точки экстремума, промежутки монотонности, точки пересечения графика с осями координат и при необходимости выбрать еще несколько контрольных точек. Именно так мы действовали в этом параграфе, когда строили графики следующих функций:
3) Полезно исследовать функцию на четность, поскольку графики четной или нечетной функции обладают симметрией (соответственно относительно оси у или относительно начала координат), и, следовательно, можно сначала построить только ветвь графика при х>0, а затем достроить симметричную ветвь. 4) Если 5) Горизонтальная асимптота характеризуется условием: если
Самый распространенный признак существования вертикальной асимптоты заключается в следующем: если 3. Найдем асимптоты. Вертикальной асимптоты нет. Для отыскания горизонтальной асимптоты надо вычислить lim f(х). Имеем:
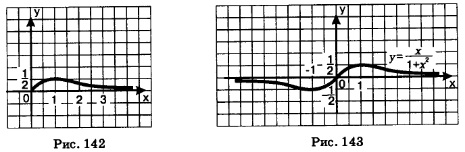
5. Составим таблицу значений функции: 6. Отметив найденные точки на координатной плоскости, соединив их плавной кривои и учтя при этом, что
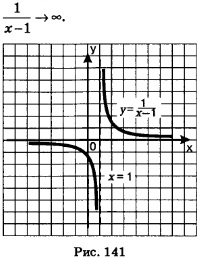
Решение. 1. Найдем область определения функции. Она задается условиями: (при значениях х = 1, х = -1 знаменатель дроби обещается в нуль). Итак,
3. Найдем асимптоты. Вертикальной асимптотой является прямая х = 1, поскольку при этом значении х знаменатель дроби обращается в нуль, а числитель отличен от нуля. Для отыскания горизонтальной асимптоты надо вычислить lim f(x). Имеем:
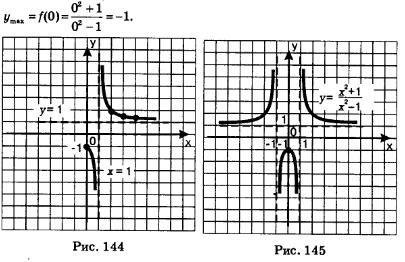
6. Отметив найденные точки на координатной плоскости, соединив их плавными кривыми, учтя при этом, что (0; -1) — точка максимума, что у = 1 — горизонтальная асимптота, что х = 1 — вертикальная асимптота, построим ветви искомого графика при х>0 (рис. 144). Добавив ветви, симметричные построенным относительно оси ординат, получим весь график (рис. 145).
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: