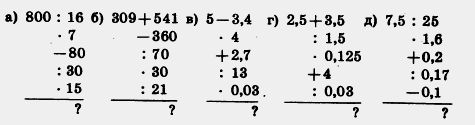|
Гипермаркет знаний>>Математика>>Математика 6 класс>>Математика: Прямая и обратная пропорциональные зависимости
22. Прямая и обратная пропорциональные зависимости
Следовательно, верна пропорция 4:2 = 56:28. Такие величины, как время работы станка и число изготовленных деталей, называют прямо пропорциональными величинами. Две величины называют прямо пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая увеличивается (уменьшается) во столько же раз. Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны. Пусть путь из города А в город В поезд со скоростью 40 км/ч проходит за 12 ч. Если скорость движения увеличить вдвое, .т. е. сделать ее равной 80 км/ч, то на этот же путь поезд затратит вдвое меньше времени, т. е. 6 ч. Во сколько раз увеличится скорость движения, во столько же раз уменьшится время движения. В этом случае отношение 80:40 будет равно не отношению 6:12, а обратному отношению 12:6. Следовательно, верна пропорция 80:40=12:6. Такие величины, как скорость и время, называют обратно пропорциональными величинами. Две величины называют обратно пропорциональными, если при увеличении (уменьшении) одной из них в несколько раз другая уменьшается (увеличивается) во столько же раз. Если величины обратно пропорциональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины. Задачи на пропорциональные величины можно решить с помощью пропорции. Задача 1. За 3,2 кг товара заплатили 11,52 р. Сколько следует заплатить за 1,5 кг этого товара? Решение. Запишем кратко условие задачи в виде таблицы, обозначив буквой х стоимость (в рублях) 1,5 кг этого товара. Запись будет иметь следующий вид:
Запишем пропорцию:
Решение. Обозначив буквой х ширину (в метрах) второго прямоугольника, запишем кратко условие задачи:
К 766. Определите, является ли прямой пропорциональной, обратной пропорциональной, или не является пропорциональной зависимость между величинами: а) путем, пройденным автомашиной с постоянной скоростью, и временем ее движения; б) стоимостью товара, купленного по одной цене, и его количеством; в) площадью квадрата и длиной его стороны; г) массой стального бруска и его объемом; д) числом рабочих, выполняющих с одинаковой производительностью труда некоторую работу, и временем выполнения этой работы; е) стоимостью товара и его количеством, купленным на определенную сумму денег; ж) возрастом человека и размером его обуви; з) объемом куба и длиной его ребра; и) периметром квадрата и длиной его стороны; к) дробью и ее знаменателем, если числитель не изменяется; л) дробью и ее числителем, если знаменатель не изменяется. Задачи 767—778 решите, составив пропорцию. 767. Стальной шарик объемом 6 см3 имеет массу 46,8 г. Какова масса шарика из той же стали, если его объем 2,5 см3? 768. Из 21 кг хлопкового семени получили 5,1 кг масла. Сколько масла получится из 7 кг хлопкового семени? 769. Для строительства стадиона 5 бульдозеров расчистили площадку за 210 мин. За какое время 7 бульдозеров расчистят эту площадку? 770. Для перевозки груза потребовалось 24 машины 1рузо- подъемностыо 7,5 т. Сколько нужно машин грузоподъемностью 4,5 т, чтобы перевезти тот же груз? 771. Для определения всхожести семян посеяли горох. Из 200 посеянных горошин взошло 170. Какой процент горошин дали всходы (процент всхожести)? 772. Во время воскресника по озеленению города на улице посадили липы. Принялось 95% всех посаженных лип. Сколько посадили лип, если принялось 57 лип? 773. В лыжной секции занимаются 80 учащихся. Среди них 32 девочки. Какой процент участников секции составляют девочки и какой мальчики? 774. Колхоз по плану должен засеять 980 га кукурузой. Но план выполнили на 115%. Сколько гектаров кукурузы посеял колхоз? 775. За 8 месяцев рабочий выполнил 96% годового плана. Сколько процентов годового плана выполнит рабочий за 12 месяцев, если будет работать с той же производительностью? 776. За три дня было убрано 16,5% всей свеклы. Сколько потребуется дней, чтобы убрать 60,5% всей свеклы, если работать с той же производительностью? 777. В железной руде на 7 частей железа приходится 3 части примесей. Сколько тонн примесей в руде, которая содержит 73,5 т железа? 778. Для приготовления борща на каждые 100 г мяса надо взять 60 г свеклы. Сколько свеклы надо взять на 650 г мяса? П 779. Вычислите устно:
782. Средние члены пропорции 6 и 10. Какими могут быть крайние члены? Приведите примеры. 783. При каком значении х верна пропорция:
785. Где на координатном луче должно быть расположено число с, чтобы была верна пропорция
790. Длина отрезка АВ равна 8 дм, а длина отрезка CD равна 2 см. Найдите отношение длин отрезков АВ и CD. Какую часть длины отрезка А В составляет длина отрезка CD? 791. Путевка в санаторий стоит 460 р. Профсоюз оплачивает 70% стоимости путевки. Сколько за путевку заплатит отдыхающий? 792. Найдите значение выражения: 1) При обработке детали из отливки массой 40 кг в отходы ушло 3,2 кг. Какой процент составляет масса детали от массы отливки? 2) При сортировке зерна из 1750 кг в отходы ушло 105 кг. Какой процент зерна остался? 794. Найдите значение выражения: 1) 6,0008:2,6 + 4,23 • 0,4; 2) 2,91 • 1,2 + 12,6288:3,6. Д 795. Из 20 кг яблок получается 16 кг яблочного пюре. ^^ Сколько яблочного пюре получится из 45 кг яблок? 796. Трое маляров могут закончить работу за 5 дней. Для ускорения работы добавили еще двух маляров. За какое время они закончат работу, считая, что все маляры будут работать с одинаковой производительностью? 797. За 2,5 кг баранины заплатили 4,75 р. Сколько баранины можно купить по той же цене на 6,65 р.? 798. В сахарной свекле содержится 18,5% сахара. Сколько сахара содержится в 38,5 т сахарной свеклы? Ответ округлите до десятых долей тонны. 799. В семенах подсолнечника нового сорта содержится 49,5% масла. Сколько килограммов таких семян надо взять, чтобы в них содержалось 29,7 кг масла? 800. В 80 кг картофеля содержится 14 кг крахмала. Найдите процентное содержание крахмала в таком картофеле. 801. В семенах льна содержится 47% масла. Сколько масла содержится в 80 кг семян льна? 802. Рис содержит 75% крахмала, а ячмень 60%. Сколько надо взять ячменя, чтобы в нем содержалось столько же крахмала, сколько его содержится в 5 кг риса? 803. Найдите значение выражения: а) 203,81 :(141 -136,42) + 38,4:0,7 5;
Школьная библиотека онлайн, учебники и книги по всему предметам, Математика 6 класс скачать Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: