|
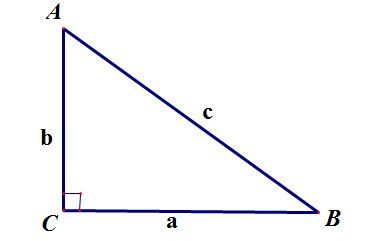
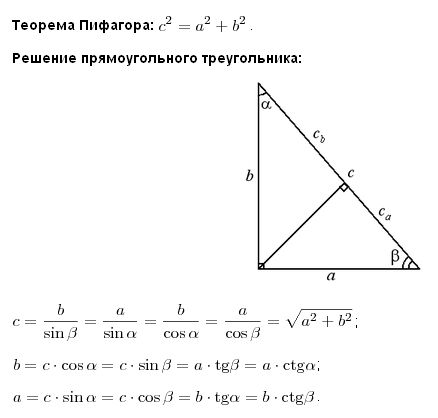
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Прямоугольный треугольник. Полные уроки Тема урокаПрямоугольный треугольник Цель урока• Проверить у школьников методом опроса знания об усвоенной теме «Треугольник»; Задачи урока• Закрепить знания учеников о треугольниках и их свойствах; План урока1. Прямоугольный треугольник. Прямоугольный треугольникУ любого прямоугольного треугольника имеется один угол, который равен 90 градусов. Сторона, которая противоположна прямому углу, имеет название гипотенузы. Гипотенуза является самой большой стороной этого треугольника. Катетами прямоугольного треугольника называются две другие его стороны. Теорема Пифагора: Для прямоугольных треугольников справедлива теорема Пифагора, согласно которой сумма квадратов катетов равна квадрату гипотенузы. ТреугольникТреугольник в геометрии представляет одну из основных фигур. Из предыдущих уроков вы знаете, что треугольник – это многоугольная фигура, которая имеет три угла и три стороны.
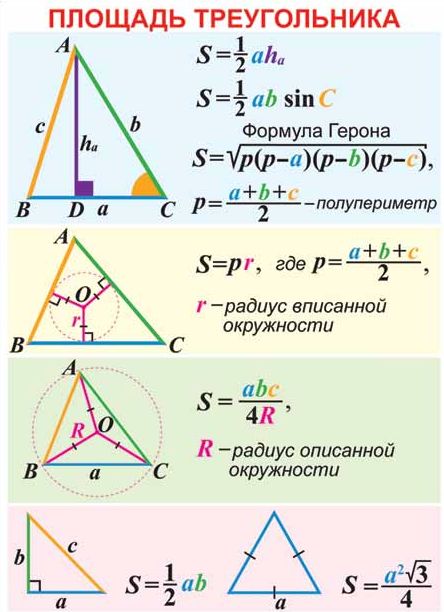
Задание • Вспомните и ответьте, что является вершинами треугольника? Основные обозначения и формулы треугольникаСвойства и особенности прямоугольных треугольниковI – е свойство. В прямоугольном треугольнике сумма его острых углов равна 90°. Против большей стороны треугольника лежит больший угол, а против большего угла лежит большая сторона. В прямоугольном треугольнике наибольшим углом, является прямоугольный угол. Если же в треугольнике самый большой угол имеет более 90°, то такой треугольник перестает быть прямоугольным, так как сумма всех углов превысить 180 градусов. Со всего этого следует, что гипотенуза является наибольшей стороной треугольника. II – е свойство. Катет прямоугольного треугольника, который лежит против угла в 30 градусов, равен половине гипотенузе. III – е свойство. Если же в прямоугольном треугольнике катет равняется половине гипотенузы, то и угол, который лежит напротив данного катета будет равен 30 градусам.
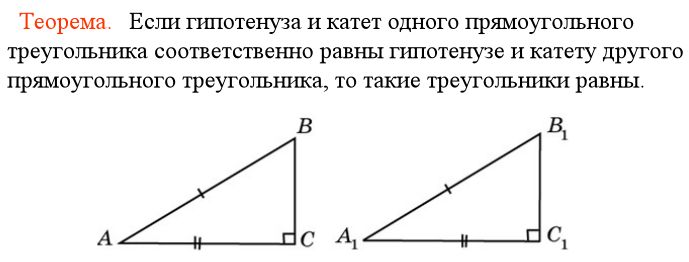
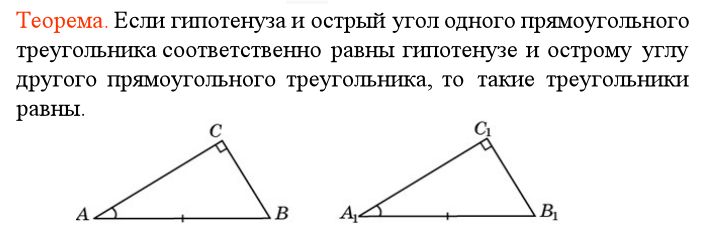
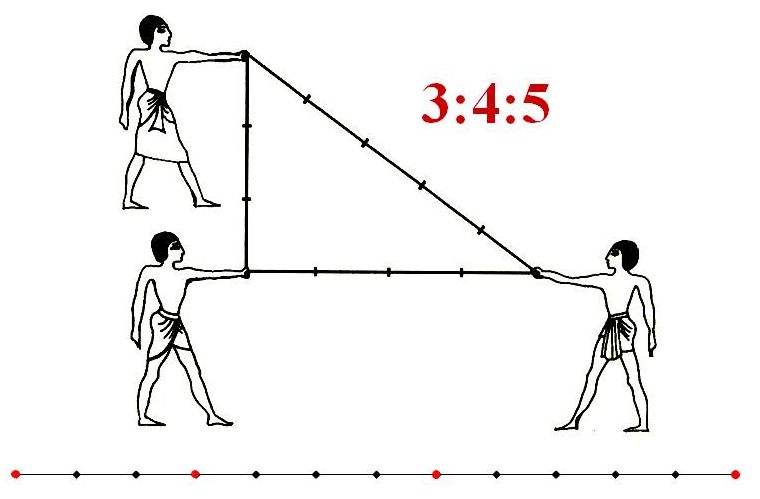
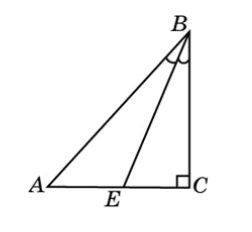
Признаки прямоугольного треугольникаПризнак 1 Признак 2 Интересные факты о теореме Пифагора• А известно ли вам, что по книге рекордов Гиннеса теорема Пифагора имеет наибольшее число доказательств теоремы и насчитывает их более трех сот. • А знаете ли вы, что среди всех доказательств теоремы Пифагора существует одно неизвестное доказательство и это доказательство самого автора теоремы, так как оно принадлежит не Пифагору, а Евклиду. • А представляете ли вы, что оказывается теорема Пифагора, была известна во многих странах еще задолго до древнегреческого философа. • Один голландский математик пришел к выводу, что заслугой Пифагора не является открытие математики, а ее обоснование и систематизация. • Происхождение «пифагоровых штанов», вроде как понятно, так как построенные на сторонах треугольника квадраты, которые расходятся в разные стороны, напоминают покрой мужских штанов. Но загадка в другом, оказывается, что в древние греки не знали что такое «штаны», да и сам Пифагор их никогда не носил. Из истории математикиИзображения треугольников и задачи с их применением можно найти на папирусах, найденных в Древней Греции и Египте. Древние мудрецы для облегчения задач стали применять определенные знаки, обозначая ими геометрические фигуры. Так еще в первом веке Герон вместо слов стал использовать треугольник. Немного позже эта геометрическая фигура одной из первых появилась в изображении орнаментов древних цивилизаций. Даже в Вавилонской геометрии, такая фигура, как прямоугольный треугольник занимала очень важное и почетное место. Впервые о нем упоминается в папирусе Ахмеса. Среди этих прямоугольных треугольников широкое значение имеет египетский треугольник. Что же это за такой египетский треугольник? Оказывается, в египетской архитектуре для построения прямых углов применялось такое соотношение сторон, как 3:4:5. Само название «египетский треугольник» появилось очень давно, вероятно еще в V веке до н.э. Это название произошло именно из Древнего Египта, так местное население широко применяло такой тип треугольника в повседневной жизни и различных сферах деятельности. Архитекторы и землемеры того времени, чтобы построить прямой угол использовали веревку, которую делили узлами или отметками на двенадцать частей, то есть три плюс четыре и плюс пять. Такой своеобразный треугольник образовывался благодаря натяжению шнура и показывал весьма точную прямоугольную форму, в котором катеты играли роль направляющих для использования в кладке прямого угла нужного сооружения. Благодаря такому изобретению, египетские строители теперь могли более точно делать расчеты для разметки земли под хозяйственные работы и применять их при строительстве пирамид. Египетский треугольник так же имеет некоторые отличительный особенности. Например, все его стороны и площадь представляю собой целый числа, из-за его прямоугольности он активно применяется в строительстве для отмерения прямых углов. К тому этот уникальный треугольник легко строиться с помощью обыкновенной веревки, как изображено на рисунке. Но самым важным в феномене египетского треугольника было то, что именно его необычные свойства подтолкнули Пифагора к попытке обобщить каким-то образом все другие прямоугольные треугольники, что и стало в итоге известно под названием теоремы Пифагора! Задание: Где еще в повседневной жизни можно встретить треугольник? Домашнее заданиеПродолжите предложение вместо точек: 1. Треугольник называется прямоугольным, если …. Дайте ответы на поставленные вопросы: 1. Какие стороны называются катетами? Может ли прямоугольный треугольник иметь: 1. стороны, равные 8, 10, 10? Задачи: 1. Чему будет равна гипотенуза прямоугольного треугольника, если его стороны равны: 6 см, 8 см, 10 см. 2. Мы имеем прямоугольный треугольник АВС, где угол С прямой. В треугольнике проведена биссектриса ВЕ. Найдите и докажите какой из отрезков больше АЕ или СЕ?
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: