Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Равновеликие тела

Равновеликие тела

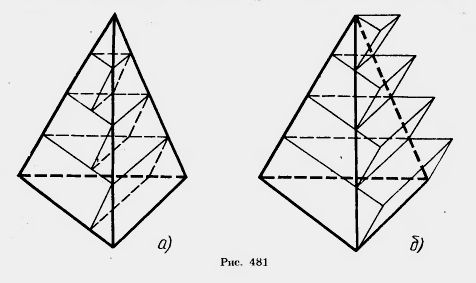
Два тела называются равновеликими, если они имеют равные объемы.

Две треугольные пирамиды с равными площадями оснований и равными высотами равновелики.

Действительно, пусть треугольные пирамиды имеют равные площади оснований и равные высоты. Докажем, что они равновелики, т. е. имеют равные объемы.

Разделим высоту каждой пирамиды на n равных частей и проведем через точки деления плоскости, параллельные основаниям. Эти плоскости разбивают пирамиду на n слоев. Для каждого слоя первой пирамиды построим содержащуюся в нем призму, как показано на рисунке 481, а. Для каждого слоя второй пирамиды построим призму, содержащую слой (рис. 481, б). Призма в k-м (считая от вершины) слое первой пирамиды и призма, содержащая (k —1)-й слой второй пирами-
 


 
ды, имеют равные площади оснований, так как эти основания подобны основаниям пирамид и коэффициент подобия один и тот же Так как у этих призм и высоты одинаковы , то они имеют равные объемы.

Пусть V₁ и V₂ — объемы пирамид, а V'₁ и V'₂ — суммы объемов построенных для них призм. Так как объем призмы в k-м слое первой пирамиды равен объему призмы (k — 1)-го слоя второй пирамиды, то сумма объемов всех призм для первой пирамиды равна сумме объемов призм всех слоев второй пирамиды, кроме   последнего.   Объем   призмы   последнего   слоя  равен S—, где S — площадь основания пирамиды, а H — высота.

Отсюда следует, что . Так как, кроме того, . Это неравенство выполняется при любом сколь угодно большом n.

А это возможно только при V₂—V₁O, т. е. при V₂V₁ Поменяв ролями пирамиды, получим противоположное неравенство V₂V₁,. А отсюда следует, что V₁=V₂. Утверждение доказано.

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений

_{Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать}

Содержание урока
 конспект урока                       
 опорный каркас  
 презентация урока
 акселеративные методы 
 интерактивные технологии 

Практика
 задачи и упражнения 
 самопроверка
 практикумы, тренинги, кейсы, квесты
 домашние задания
 дискуссионные вопросы
 риторические вопросы от учеников

Иллюстрации
 аудио-, видеоклипы и мультимедиа 
 фотографии, картинки 
 графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты

Дополнения
 рефераты
 статьи 
 фишки для любознательных 
 шпаргалки 
 учебники основные и дополнительные
 словарь терминов                          
 прочие 

Совершенствование учебников и уроков
 исправление ошибок в учебнике
 обновление фрагмента в учебнике 
 элементы новаторства на уроке 
 замена устаревших знаний новыми 

Только для учителей
 идеальные уроки 
 календарный план на год  
 методические рекомендации  
 программы
 обсуждения


Интегрированные уроки

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.