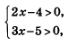|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Равносильность уравнений
Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Например, уравнения равносильны, оба они имеют по два корня: 2 и -2. Равносильны и уравнения поскольку оба они не имеют корней.
f(х) = g(х) (1) является в то же время корнем уравнения р(x) = h(х), (2) то уравнение (2) называют следствием уравнения (1). Например, уравнение x-2 =3 имеет корень х = 5, а уравнение (х-2)2 =9 имеет два корня: х1 =5, х2 = -1. Корень уравнения х~2=3 является одним из корней уравнения (х-2)2 =9. Значит, уравнение (х-2)2 =9 — следствие уравнения х-2 =3. Достаточно очевидным является следующее утверждение: Два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого. (1) -(2) -(3) -(4) -»... В конце концов получают достаточно простое уравнение и находят его корни. В этот момент и возникает главный вопрос: совпадает ли множество найденных корней последнего уравнения с множеством корней исходного уравнения (1)? Если все преобразования были равносильными, т.е. если были равносильны уравнения (1) и (2), (2) и (3), (3) и (4) и т.д., то ответ на поставленный вопрос положителен: да, совпадает. Это значит, что, решив последнее уравнение цепочки, мы тем самым решим и первое (исходное) уравнение цепочки. Если же некоторые преобразования были равносильными, а в некоторых мы не^уверены, но точно знаем, что переходили с их помощью к уравнениям-следствиям, то однозначного ответа на поставленный вопрос мы не получим. Чтобы ответ на вопрос был более определенным, нужно все найденные корни последнего уравнения цепочки проверить, подставив их поочередно в исходное уравнение (1). Если проверка показывает, что найденный корень последнего уравнения цепочки не удовлетворяет исходному уравнению, его называют посторонним корнем', естественно, что посторонние корни в ответ не включают. Вы, конечно, понимаете, что термин «более простое уравнение» вообще говоря, не поддается, точному описанию. Обычно считают одно уравнение более простым, чем другое, по чисто внешним признакам. Например, решая уравнение Первый этап— технический. На этом этапе осуществляют преобразования по схеме (1) —»(2) —»(3) —>(4) —»... и находят корни последнего (самого простого) уравнения указанной цепочки. Второй этап— анализ решения. На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными. Третий этап— проверка. Если анализ, проведенный на втором этапе, показывает, что некоторые преобразования могли привести к уравнению-следствию, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.
1. Как узнать, является ли переход от одного уравнения к другому равносильным преобразованием?
1. Теоремы о равносильности уравнений. Решение уравнений, встречающихся в школьном курсе алгебры, основано на шести теоремах о равносильности (все они в той или иной мере вам известны). Первые три теоремы — «спокойные», они гарантируют равносильность преобразований без каких-либо дополнительных условий, их использование не причиняет решающему никаких неприятностей.
а) имеет смысл всюду в области определения (в области допустимых значений) уравнения f(х) = g(х); Замечание 1. Следствием теоремы 4 является еще одно «спокойное» утверждение: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
равносильно уравнению f(х) = g(x). 2. Преобразование данного уравнения в уравнение-следствие. В этом пункте мы ответим на второй вопрос: какие преобразования переводят данное уравнение в уравнение-следствие? Частично ответ на этот вопрос связан с тремя последними теоремами. Можно сказать так: если в процессе решения уравнения мы применили заключение одной из теорем 4, 5, 6, не проверив выполнения ограничительных условий, заложенных в формулировках теорем, то получится уравнение-следствие. Приведем примеры. 1) Уравнение х-1=3 имеет один корень х = 4. Умножив обе части уравнения на х-2, получим уравнение(g;-1)(g; -2) = 3(х-2), имеющее два корня: (x) =4 и х2 =2. Второй корень является посторонним для заданного уравнения. Причина его появления состоит в том, что мы умножили обе части уравнения на одно и то же выражение, нарушив при этом условия теоремы 4. В этой теореме содержится требование: выражение, на которое мы умножаем обе части уравнения, нигде не должно обращаться в 0. Мы же умножили обе части уравнения на выражение х-2, которое обращается в 0 при х=2; именно это значение оказалось посторонним корнем. 2) Возьмем то же самое уравнение х-1=3 и возведем обе его части в квадрат. Получим уравнение (х-1)2 =9, имеющее два корня: хг =4, хг =-2. Второй корень является посторонним для уравнения х-1 = 3 Причина его появления состоит в том, что мы возвели обе части уравнения в одну и ту же четную степень, нарушив при этом условие теоремы 5. В этой теореме содержится требование: обе части уравнения должны быть неотрицательны. Про выражение х-1 этого утверждать мы не можем. 3) Рассмотрим уравнение ln(2х-4) =ln(Зх-5). Потенцируя, получим уравнение 2х-4 = Зх-5 с единственным корнем х = 1. Но этот корень является посторонним для заданного логарифмического уравнения, поскольку оба выражения под знаками логарифмов при х = 1 принимают отрицательные значения. Причина появления постороннего корня состоит в том, что мы, потенцируя (т.е. «освобождаясь» от знаков логарифмов), нарушили условия теоремы 6. В этой теореме содержится требование: выражения под знаками логарифмов должны быть положительными; о выражениях 2х-4и Зх-5этого утверждать мы не можем, так как они при одних значениях х положительны, при других — отрицательны. В последнем примере переход от логарифмического уравнения к уравнению 2х-4=3х-5 привел к расширению области определения уравнения. Область определения логарифмического уравнения задается системой неравенств: решив которую находим: х > 2. Область же определения уравнения 2х-4 = Зх-5 есть множество всех действительных чисел. По сравнению с логарифмическим уравнением ощ расширилась: добавился луч Перечислим возможные причины расширения области определения уравнения:
1) произошло расширение области определения уравнения; А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: