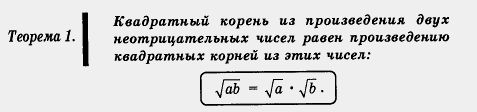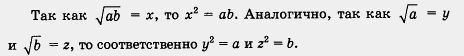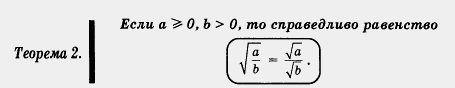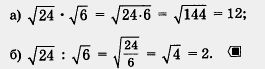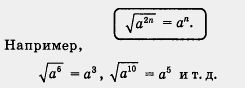|
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Свойства квадратных корней
Свойства квадратных корней
До сих пор мы осуществляли над числами пять арифметических операций: сложение, вычитание, умножение, деление и возведение в степень, причем при вычислениях активно использовали различные свойства этих операций, например а + b = b + а, аn-bn = (аb)n и т.д.
В этой главе введена новая операция — извлечение квадратного корня из неотрицательного числа. Чтобы успешно ее использовать, нужно познакомиться со свойствами этой операции, что мы и сделаем в настоящем параграфе.
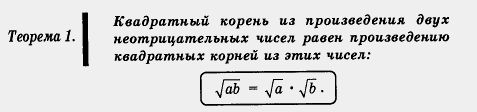
Доказательство. Введем следующие обозначения: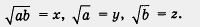
Нам надо доказать, что для неотрицательных чисел х, у, z выполняется равенство х = yz.
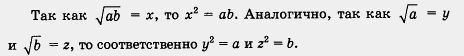
Итак, х2 = ab, у2 = а, z2 = b. Тогда х2 = y2z2, т. е. х2 = (yz)2.
Если квадраты двух неотрицательных чисел равны, то и сами числа равны, значит, из равенства х2 = (yz)2 следует, что х = yz, а это и требовалось доказать.
Приведем краткую запись доказательства теоремы:

Замечание 1. Теорема остается справедливой и для случая, когда подкоренное выражение представляет собой произведение более чем двух не отрицательных множителей.
Замечание 2. Теорему 1 можно оформить, используя конструкцию «если... , то» (как это принято для теорем в математике). Приведем соответствующую формулировку: если а и b — неотрицательные числа, то справедливо равенство 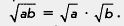 . .
Следующую теорему мы именно так и оформим.
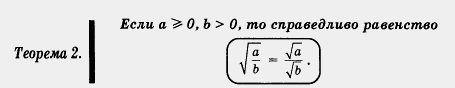
(Краткая формулировка, которую удобнее использовать на практике: корень из дроби равен дроби от корней или корень из частного равен частному от корней.)
Доказательство.
На этот раз мы приведем только краткую запись доказательства, а вы попробуйте сделать соответствующие комментарии, аналогичные тем, что составили суть доказательства теоремы 1.

Пример 1. Вычислить  . .
Решение. Воспользовавшись первым свойством квадратных корней (теорема 1), получаем
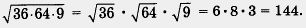
Замечание 3. Конечно, этот пример можно решить по-другому, особенно если у вас под рукой микрокалькулятор: перемножить числа 36, 64, 9, а затем извлечь квадратный корень из полученного произведения. Однако, согласитесь, предложенное выше решение выглядит более культурно.
Пример 2.


Замечание 4. При первом способе мы проводили вычисления «в лоб». Второй способ изящнее:
мы применили формулу а2 — b2 = (а — b) (а + b) и воспользовались свойством квадратных корней.
Замечание 5. Некоторые «горячие головы» предлагают иногда такое «решение» примера 3:
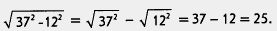
Это, конечно, неверно: вы видите — результат получился не такой, как у нас в примере 3. Дело в том, что нет свойства 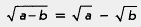 , как нет и свойства , как нет и свойства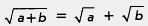 Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное. Имеются только свойства, касающиеся умножения и деления квадратных корней. Будьте внимательны и осторожны, не принимайте желаемое за действительное.
Пример 4. Вычислить: а) 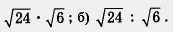
Решение. Любая формула в алгебре используется не только «справа налево», но и «слева направо». Так, первое свойство квадратных корней означает, что 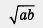 в случае необходимости можно представить в виде в случае необходимости можно представить в виде 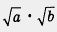 , и обратно, что , и обратно, что 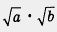 можно заменить выражением можно заменить выражением 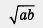 То же относится и ко второму свойству квадратных корней. Учитывая это, решим предложенный пример. То же относится и ко второму свойству квадратных корней. Учитывая это, решим предложенный пример.
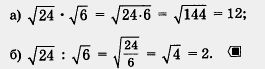
Завершая параграф, отметим еще одно достаточно простое и в то же время важное свойство:
если a > 0 и n — натуральное число, то
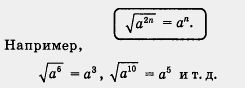
Пример 5. Вычислить 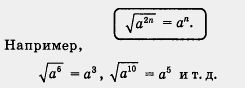 , не используя таблицу квадратов чисел и микрокалькулятор. , не используя таблицу квадратов чисел и микрокалькулятор.
Решение. Разложим подкоренное число на простые множители:

Замечание 6. Этот пример можно было решить так же, как и аналогичный пример в § 15. Нетрудно догадаться, что в ответе получится «80 с хвостиком», поскольку 802 < 7056 < 902. Найдем «хвостик», т. е. последнюю цифру искомого числа. Пока мы знаем, что если корень извлекается, то в ответе может получиться 81, 82, 83, 84, 85, 86, 87, 88 или 89. Проверить надо только два числа: 84 и 86, поскольку только они при возведении в квадрат дадут в результате четырехзначное число, оканчивающееся цифрой 6, т.е. той же цифрой, которой оканчивается число 7056. Имеем 842 = 7056 — это то, что нужно. Значит, 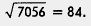
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Книги, учебники математике скачать, конспект на помощь учителю и ученикам, учиться онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|