|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Свойство диагоналей параллелограмма. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
Введение«Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия». Венгерский математик Дьердье Пойа.
Геродота от Фукидида, родившегося около 460 г. до н. э.
Московскому папирусу несколько уступает по возрасту папирус Ахмета. Он называется так по имени его египетского составителя и относится примерно к 1700 г. до н.э. Этот папирус хранится в Лондоне в Британском музее. В папирусе рассмотрены 84 прикладные задачи, в том числе 20 геометрических. Из них видно, что египтяне умели вычислять площадь квадрата, прямоугольника и трапеции, что ими была установлена формула, которая дает хорошее приближение к истинному значению площади круга. Развитие зачатков геометрии было связано и с потребностями строительства. У жителей Египта был развит культ мертвых. Египтяне верили, что душа когда-нибудь вернется к умершему, поэтому его тело необходимо сохранить, забальзамировав и поместив в надежную гробницу. А так как человеку в загробном царстве понадобятся вещи, которыми он пользовался при жизни, в гробницу ставили мебель с посудой, укладывали одежду, оружие, украшения и даже музыкальные инструменты. Самые величественные гробницы для правителей Египта — фараонов — строились в виде гигантских пирамид из каменных блоков. Они считались символом вечности, поэтому египтяне с гордостью говорили: «Все подвластно времени, но само время боится пирамид». Ко времени строительства пирамид и относят зарождение практической геометрии, которая с течением времени постепенно развилась в науку. Слово «геометрия» пришло к нам из Греции. Оно составлено из двух слов: «гео», что в переводе на русский язык означает «земля», и «метрио» — «мерю». Само слово «геометрия» указывает на практическое происхождение науки. Но однажды им пришлось устыдиться, потому что пришелец из далекой Греции оказался намного искуснее их. Египтяне задали ему трудную задачу: определить высоту пирамиды. Он нашел простое и красивое решение- воткнул длинную палку вертикально в землю и сказал: «Когда тень от палки будет равна ее длине, тогда тень от пирамиды будет иметь, ту же длину, что и высота пирамиды». Фараон и его приближенные были изумлены,- как точно и быстро, без специальных приборов северный пришелец решил трудную задачу. Это был Фалес Милетский.
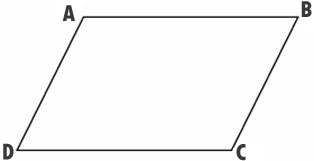
Основные понятияИзвестны некоторые виды параллелограмма:
Прямоугольник
Ромб Слово «ромб» тоже греческого происхождения, оно означало в древности вращающееся тело, веретено, юлу. Ромб связывали первоначально с сечением, проведенным в обмотанном веретене. Квадрат Термин «квадрата» происходит от латинского quadratum (quadrare - сделать четырехугольным), перевод с греческого “тетрагонон” - четырехугольник.
Свойства параллелограммаСвойство противолежащих сторон параллелограммаУ параллелограмма противолежащие стороны равны. Доказательство. Свойство противолежащих углов параллелограммаУ параллелограмма противолежащие углы равны. Доказательство. Свойство диагоналей параллелограммаДиагонали параллелограмма пересекаются и точкой пересечения делятся пополам. Доказательство. В учебниках для обычных школ (например, в Погорелове) доказывается она так: диагонали делят параллелограмм на 4 треугольника. Рассмотрим одну пару и выясним - они равны: основания у них - противоположные стороны, прилежащие к нему соответствующие углы равны как вертикальные при параллельных прямых. То есть отрезки диагоналей попарно равны. Всё. Всё ли? Забавно, что доказать эту часть намного сложнее. Следует это, кстати, из более общего результата: у любого выпуклого четырёхугольника диагонали будут пересекаться, у любого невыпуклого - не будут. Диагонали параллелограмма - одно из очень красивых мест школьной математики. Вроде бы всё совершенно очевидно на первый взгляд - но попробуй доказать.
Примеры решения задачЗадача №1В параллелограмме АВСD на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.
Решение. Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
Задача №2В параллелограмме ABCD диагональ BD = 6 см и образует со сторонами AD и DC углы по 60 градусов. Определите углы и периметр параллелограмма ABCD. Поскольку нам дана величина угла ADB (диагональ параллелограмма образует со сторонами AD и DC углы по 60 градусов), то величина угла DBC также равна 60 градусов, поскольку противоположные стороны параллелограмма параллельны, соответственно диагональ является секущей для двух параллельных прямых AD и BC, а для любой секущей внутренние накрест лежащие углы равны. Таким образом, в треугольнике BCD нам известны два угла из трех, и они оба равны 60 градусов. Соответственно, поскольку сумма углов треугольника равна 180 градусов, то угол BCD также равен 60 градусам, из чего следует, что треугольник BCD - равносторонний. Поскольку треугольник BCD - равносторонний, то BC = CD = BD = 6 см. Таким образом, поскольку противолежащие стороны параллелограмма равны, периметр его равен 24 см. Параллелограмм является ромбом. Задача №3На диагонали МР прямоугольника МNРQ отложены равные отрезки МА и РВ. Докажите, что АNBQ параллелограмм. Четырехугольник является параллелограммом, если его противоположные стороны попарно равны. Докажем это. Исходя из условия задачи треугольники MAN и PBQ равны. Так как PB = AM по условию задачи, PQ = NM как противоположные стороны прямоугольника, а углы BPQ и NMA равны, как внутренние накрест лежащие для параллельных прямых NP и MQ и секущей MP. Аналогично доказывается равенство треугольников NBP и QAM. Поскольку описанные треугольники равны, то NA = BQ, NB = BQ. Таким образом, поскольку противолежащие стороны равны, то АNBQ параллелограмм.
Задача №4Попробуйте составить квадрат из набора палочек: 6 шт. по 1 см, 3 шт. по 2 см, 6 шт. по 3 см и 5 шт. по 4 см. Ломать палочки и накладывать одну на другую нельзя. Решение. Такой квадрат составить нельзя, поскольку его периметр должен быть 50 см, т.е. стороны не являются целыми числами. Ответ: Этого сделать нельзя.
Самостоятельная проверка
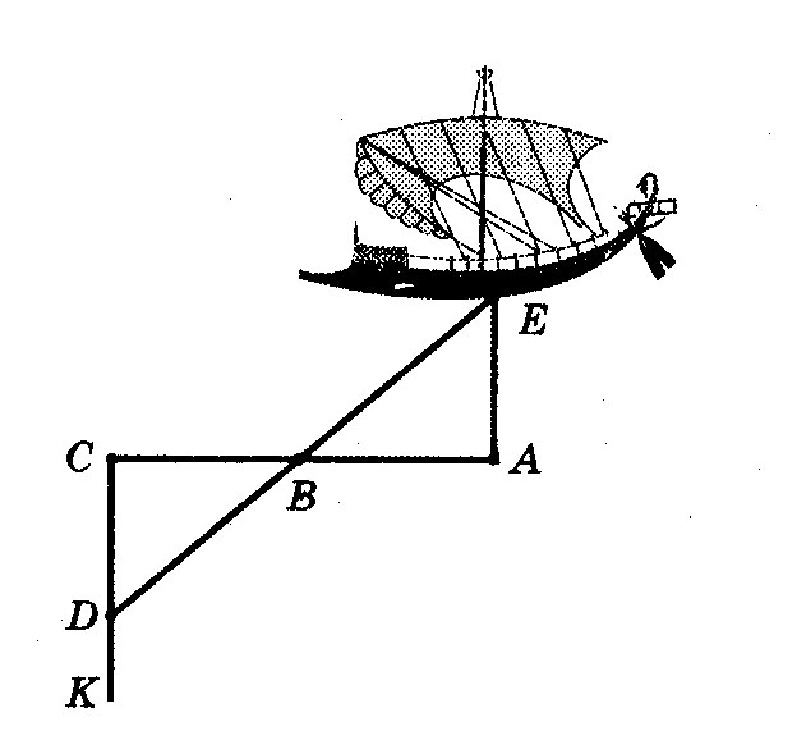
Интересный фактФалеса из города Милета. Фалеса из города Милета в Малой Азии, родившегося в VI в. до н.э., считают отцом греческой математики. Фалес прожил долгую и, несомненно, яркую жизнь. Его родители принадлежали к торговой аристократии. В молодости Фалес был купцом и путешественником, а в старости считался одним из семи величайших греческих мудрецов. Отправившись по торговым делам в Египет, он пробыл там несколько лет и настолько глубоко изучил достижения египетских жрецов, что вскоре превзошел их в знаниях. Будучи философом, он стремился разумно, логически объяснять все явления. Применяя этот подход к математике, он требовал не только ограничиваться формулировкой тех или иных утверждений, но и находить их доказательства. С именем Фалеса Милетского связывается появление доказательств некоторых теорем геометрии. К их числу относятся: — теорема о равенстве вертикальных углов; — о равенстве углов при основании равнобедренного треугольника; — о равенстве треугольников по стороне и двум прилежащим к ней углам (второй признак равенства треугольников) и другие. Теореме о равенстве двух треугольников по стороне и двум прилежащим к ней углам Фалес нашел важное практическое применение. В гавани Милета был построен дальномер, определяющий расстояние до корабля в море. Он представлял собой три вбитых колышка А, В и С (АВ = ВС) и размеченную прямую СК, перпендикулярную .СА. При появлении корабля на прямой СК находили точку D такую, чтобы точки D, .В и Е оказывались на одной прямой. Как ясно из чертежа, расстояние CD на земле является искомым расстоянием до корабля.
Вопросы
Список использованных источников
Над уроком работали Кузнецов А. В. Потурнак С.А. Евгений Петров Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: