|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Свойство медианы равнобедренного треугольника. Полные уроки ТЕМА УРОКА: Свойство медианы равнобедренного треугольника . Цели урока:
План урока:
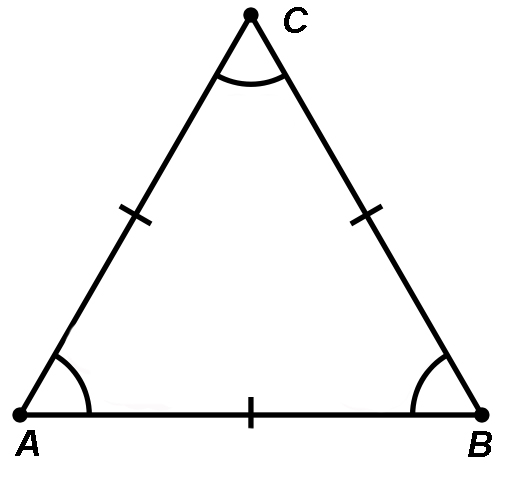
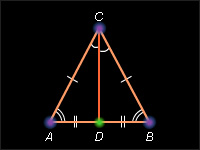
Файл:O.gif Треугольник называетсяравнобедренным, если у него две стороны равны. Эти стороны называются боковыми, а третья сторона – основанием. Файл:T.gif В равнобедренном треугольнике углы при основании равны. Пусть Δ ABC – равнобедренный с основанием AB. Рассмотрим Δ BAC . По первому признаку эти треугольники равны. Действительно, AC = BC; BC = AC; Файл:16122010 13.gifC = Файл:16122010 13.gifC. Отсюда следует Файл:16122010 13.gifA = Файл:16122010 13.gifB как соответствующие углы равных треугольников. Теорема доказана. Пусть Δ ABC – треугольник, в котором A = B. Δ ABC равен Δ BAC по второму признаку равенства треугольников. Действительно: AB = BA; B = A; A = B. Из равенства треугольников следует равенство соответствующих его сторон: AC = BC. Тогда, по определению, Δ ABC – равнобедренный. Теорема доказана. Пусть Δ ABC– равнобедренный с основанием AB, и CD – медиана, проведенная к основанию. В треугольниках CAD и CBD углы CAD и CBD равны, как углы при основании равнобедренного треугольника (по теореме 4.3), стороны AC и BC равны по определению равнобедренного треугольника, стороны AD и BD равны, потому что D – середина отрезка AB. Отсюда получаем, что Δ ACD = Δ BCD. Из равенства треугольников следует равенство соответствующих углов: Файл:16122010 13.gifACD = Файл:16122010 13.gifBCD, Файл:16122010 13.gifADC = Файл:16122010 13.gifBDC. Из первого равенства следует, что CD – биссектриса. Углы Файл:16122010 13.gifADC и Файл:16122010 13.gifBDC смежные, и в силу второго равенства они прямые, поэтому CD – высота треугольника. Теорема доказана.
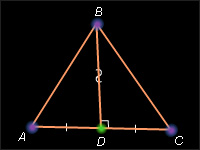
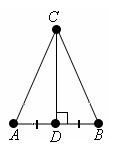
В треугольнике ABC проведем медиану BD, которая по условию также является высотой. Прямоугольные треугольники ABD и CBD равны, т. к. катет BD общий, AD = CD по построению. Следовательно, гипотенузы этих треугольников равны как соответственные элементы равных треугольников, т. е. AB = BC. Теорема доказана. Пусть в треугольнике ABC CD медиана и высота.
Свойство медианы равнобедренного треугольника. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой. Дано: А АВС — равнобедренный треугольник, АВ — основание, CD — медиана Доказать: CD — биссектриса и высота. Доказательство. Треугольники CAD и CBD равны но второму признаку равенства треугольников (стороны АС и ВС равны, так как АВС — равнобедренный. Углы CAD и CBD равны как углы при основании равнобедренного треугольника. Стороны AD и BD равны, поскольку D — середина отрезка АВ). Из равенства треугольников CBD и CAD следует равенство углов: Так как углы ACD и BCD равны, то CD — биссектриса. Поскольку углы ADC и BDC смежные и равны друг другу, они прямые. Следовательно, отрезок CD является также высотой треугольника АВС. Теорема доказана. Таким образом, установлено, что биссектриса, медиана и высота равнобедренного треугольника, проведенные к основанию, совпадают. Поэтому справедливы также следующие утверждения: 1. Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой. 2. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
Интересный факт: Геометрия Вселенной, Большой взрыв и расширение Вселенной
Вопросы:
Список использованных источников:
Отредактировано и выслано Потурнаком С. А. Над уроком работали Потурнак С. А.
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: