|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Свойство углов, образованных при пересечении параллельных прямых секущей. Полные уроки
Цели урока:
Задачи урока
План урока:
Повторение:Вспомнить взаимное расположение прямых на плоскости. Две прямые могут пересекаться (в одной точке) или на пересекаться (параллельны).
Файл:01022011 0.gifФайл:01022011 1.gif Файл:O.gif Две прямые на плоскости называются параллельными, если они не пересекаются. В евклидовой геометрии. Параллельными (иногда — равнобежными) прямыми называются прямые, которые лежат в одной плоскости и либо совпадают, либо не пересекаются. (В некоторых школьных определениях совпадающие прямые не считаются параллельными, здесь такое определение не рассматривается). Через любую точку можно провести ровно одну прямую, параллельную данной. Это отличительное свойство евклидовой геометрии, в других геометриях число 1 заменено другими (в геометрии Лобачевского таких прямых минимум две). Используя аксиоматику Вейля и векторный подход для построения Евклидовой геометрии, параллельность прямых можно определить так: Две прямые называются параллельными, если направляющие их векторы коллинеарны. Основные теоремы о параллельных прямых
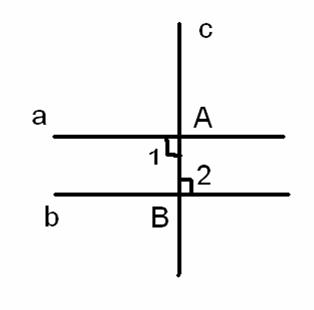
1) она пересекает и другую прямую. Вспомним, что две прямые, перпендикулярные третьей, не пересекаются. Признаки параллельности двух прямыхПрямая с называется секущей ми отношению к прямым а и b, если она пересекает их в двух точках. При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 3 обозначены цифрами. Некоторые пары этих углов имеют специальные названия: накрест лежащие углы: 3 и 5, 4 и 6; односторонние углы: 4 и 5, 3 и 6; соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.
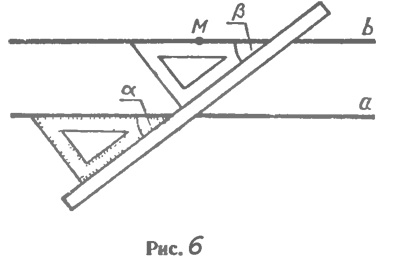
Практические способы построения параллельных прямыхПризнаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертежного угольника и линейки. Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертежный угольник к прямой а, а к нему линейку так, как показано на рисунке 103. Затем, передвигая угольник вдоль линейки, добьемся того, чтобы точ ка М оказалась на стороне угольника, и проведем прямую b. Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами альфа и
бета, равны. Еще есть способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертежной практике. Аналогичный способ применяется при выполнении столярных работ, где для разметки параллельных прямых используется малка (две деревянные планки, скрепленные шарниром).
Свойство угловI. Если при пересечении двух прямых третьей, накрест лежащие углы равны, то такие прямые параллельны. Рассмотрим случай, когда ∠1=∠2=90° Тогда аФайл:01022011 8.gifАВ и вФайл:01022011 8.gifАВ. (Две прямые, перпендикулярные третьей, не пересекаются) Значит, а || в.II. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны 1)∠2=∠3 (вертикальные). 2) ∠1=∠2 (по условию). следует что ∠1=∠3, они накрест лежащие при пересечении прямых а и в секущей с, по первому признаку параллельности а || в. III. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны. Рисунок используем тот же что и для II свойства. 1) ∠1+∠4= 180° (по условию). 2) ∠3+∠4=180°(смежные). следует что ∠1=<3 , они накрест лежащие при пересечении прямых а и в и секущей с, по первому признаку параллельности а || в.
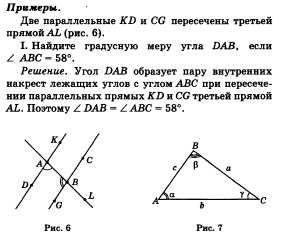
II. Найдите градусную меру угла КАВ, если ABC = 58°. Решение. Угол КАВ образует пару внутренних односторонних углов с углом ABC при пересечении параллельных прямых KD и CG третьей прямой AL. Поэтому KAB + ABC = 180°, откуда KAB = 180° - 58° = 122°. III. Найдите градусную меру угла LBC, если KAB = 122°. Решение. Угол LBC образует пару соответственных углов с углом КАВ при пересечении параллельных прямых KD и CG третьей прямой AL. Поэтому КАВ=LBC = 122°. Решение заданий на закрепление.
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: