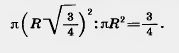|
Гипермаркет знаний>>Математика>>Математика 11 класс>>Математика:Сечение шара плоскостью
Сечение шара плоскостью
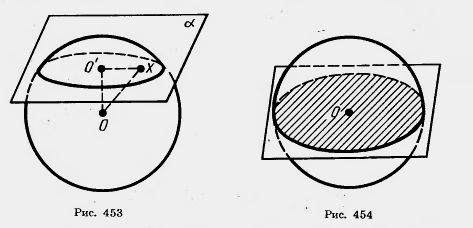
Доказательство. Пусть
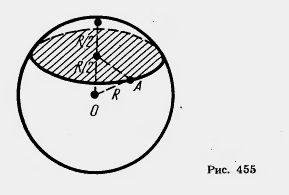
Обратно: любая точка X этого круга принадлежит шару. А это значит, что сечение шара плоскостью Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом (рис. 454), а сечение сферы — большой окружностью.
Решение. Если радиус шара R (рис. 455), то радиус круга в сечении будет Отношение площади этого круга к площади большого круга равно
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: