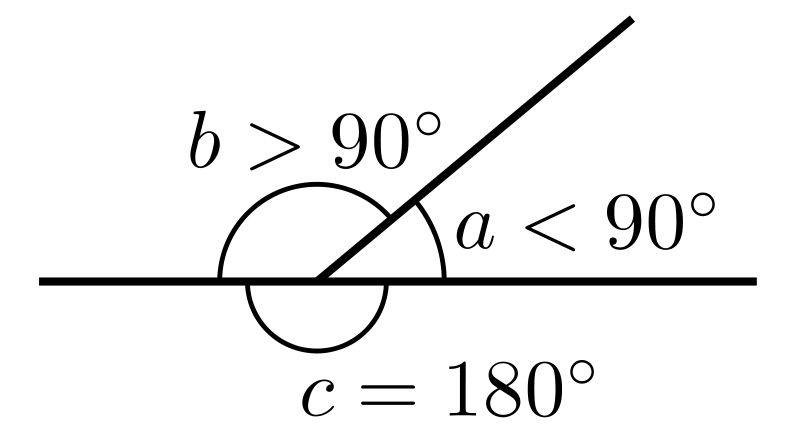|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Смежные углы. Полные уроки Смежные углы.
Что такое смежный уголУгол – это геометрическая фигура ( рис.1 ), образованная двумя лучами OA и OB ( стороны угла ), исходящими из одной точки O ( вершина угла ).
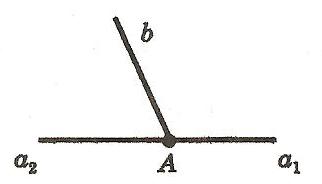
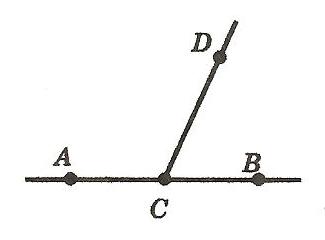
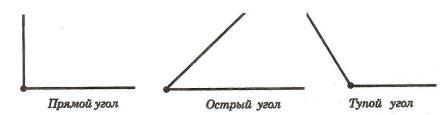
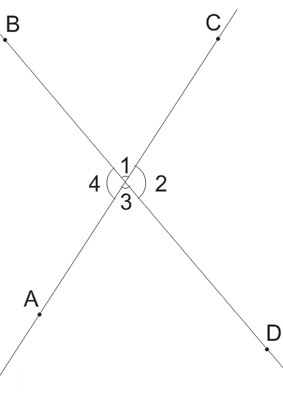
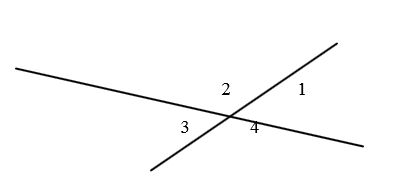
Смежные углы — (Agles adjacets) такие, которые имеют общую вершину и общую сторону. Преимущественно под этим именем подразумеваются такие углы, которых остальные две стороны лежат по противоположным направлениям одной прямой, проведенной через. На рисунке 2 углы a1b и a2b смежные. У них общая сторона b, а стороны a1, a2 — дополнительные полупрямые. На рисунке 3 изображена прямая AB, точка C расположена между точками A и B. Точка D — точка не лежащая на прямой AB. Получается, что углы BCD и ACD смежные. У них общая сторона CD, а стороны CA и CB дополнительные полупрямые прямой AB, так как точки A, B разделены начальной точкой C. Теорема о смежных углахТеорема: сумма смежных углов равна 180° Угол, равный 90° называется прямым. Из теоремы о сумме смежных углов следует, что угол, смежный с прямым углом также прямой угол. Угол, меньший 90° называется острым, а угол больше 90° — тупым. Так как сумма смежных углов равна 180°, значит угол, смежный с острым углом — тупой угол. А угол смежный с тупым углом — острый угол. Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°. Определение 1.1. Углом называют фигуру, состоящую из точки - вершины угла - и двух различных полупрямых, исходящих из этой точки, - сторон угла. Определение 2. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развернутым. Определение 3. Прямой угол - это угол величиной в 90 градусов. Определение 4. Угол, меньший 90 градусов, называется острым углом. Определение 5. Угол, больший 90 градусов и меньший 180 градусов, называется тупым углом. Определение 6. Два угла, одна сторона которых общая, а другие стороны лежат на одной прямой, называются смежными. Определение 7. Углы, стороны которых продолжают друг друга, называются вертикальными углами.
Интересный фактСвязь математики с музыкой Так же предложу вашему внимаю забавную пародию про спор двух математиков =)
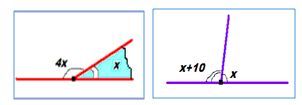
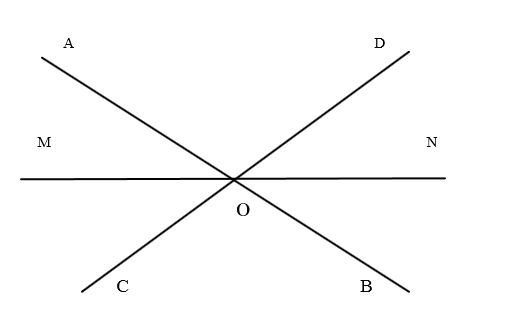
Геометрия вокруг насГеометрия в нашей жизни имеет немаловажное значение. Ввиду того, что когда оглядеться вокруг, то не сложно будет заметить, что нас окружают различные геометрические фигуры. Мы с ними сталкиваемся повсюду: на улице, в классе, дома, в парке, в спортивном зале, в школьной столовой, в принципе везде, где бы мы с вами не находились. Но темой сегодняшнего урока являются смежные угли. Поэтому давайте оглянемся вокруг и попытаемся в этом окружении найти углы. Если вы внимательно посмотрите в окно, то можете увидеть, что некоторые ветки дерева образуют смежные углы, а в перегородках на воротах можно заметить множество вертикальных углов. Приведите свои примеры смежных углов, которые вы наблюдаете в окружающей обстановке. Задание 1. 1. Вот на столе на книжной подставке стоит книга. Какой угол она образует? Задание 2. Перед вами изображена геометрическая фигура. Что это за фигура, назовите ее? А теперь назовите все смежные углы, которые вы можете увидеть на этой геометрической фигуре. Задание 3. Перед вами изображение рисунка и картины. Рассмотрите их внимательно и скажите, какие виды улов вы видите на картине, а какие углы на рисунке. Решение задач1) Даны два угла, относящиеся друг к другу как 1 : 2, а смежные с ними - как 7 : 5. Нужно найти эти углы. Математический диктант на повторение ранее выученного материала1) Выполните рисунок: прямые a I b пересекаются в точке А. Отметьте меньший из образованных углов цифрой 1, а остальные углы – последовательно цифрами 2,3,4; дополняющие лучи прямой а - через а1 и а2, а прямой b - через b1 i b2. а) угол 1 и угол …. смежные, поскольку ... Решите задачи: 1. Может ли сумма 3-х углов, образованных при пересечении 2-х прямых, равняться 100°? 370°? 3. Нужно найти угол, когда он втрое больше, чем смежный с ним. а) сумма 2-х углов из четырех 84°; Итог урока1. назовите углы, которые образуются при пересечении 2-х прямых? Домашнее задание: 1. Найдите отношение градусных мер смежных углов, когда один из них на 54° больше второго. Вопросы:
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: