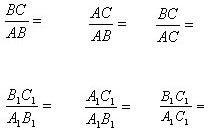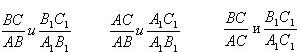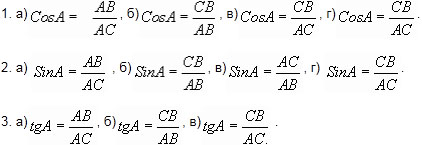|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Соотношения между сторонами и углами в прямоугольном треугольнике. Полные уроки
Тема урока
Цели урока
Задачи урока
План урока
Вступительное словоТригонометрия– математическая дисциплина, изучающая зависимость между сторонами и углами треугольника. Тригонометрия возникла из практических нужд человека. С ее помощью можно определить расстояние до недоступных предметов и вообще, существенно упростить процесс геодезической съемки местности для составления географических карт. Зачатки тригонометрических познаний зародились в древности. Важный шаг в развитии тригонометрии был сделан индийскими учеными. Окончательный вид тригонометрия приобрела в 17 веке в трудах Л.Эйлера. Индийские ученые Леонард Эйлер
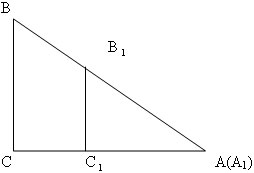
Начиная с XVII в., тригонометрические функции начали применять к решению уравнений, задач механики, оптики, электричества, радиотехники, для описания колебательных процессов, распространения волн, движения различных механизмов, для изучения переменного электрического тока и т. д. Поэтому тригонометрические функции всесторонне и глубоко исследовались, и приобрели важное значение для всей математики. В начале 9 класса на уроках физики Вы будете рассматривать некоторые вопросы: «Движение тела под углом к горизонту», «Движение тела по параболе», где необходимы умения решения прямоугольного треугольника. Какие зависимости между элементами прямоугольного треугольника вам известны? (теорема Пифагора, свойства катета, лежащего против угла в 30о) Сегодня мы познакомимся с элементами тригонометрии, необходимыми для решения прямоугольных треугольников. Изучение нового материалаЕсли в двух прямоугольниках треугольниках острые углы равныВо многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Для работы нам нужны чертежи двух прямоугольных треугольников, имеющих равные острые углы. Для облегчения этой работы воспользуемся небольшой хитростью: мы как бы «наложим» эти треугольники друг на друга. Вот так, например:
Сравните следующие отношения:
Приходим к выводу, что полученные результаты зависят от величины острого угла, но не зависят от размеров треугольника.
Если в двух прямоугольниках треугольниках острые углы равны, то отношения
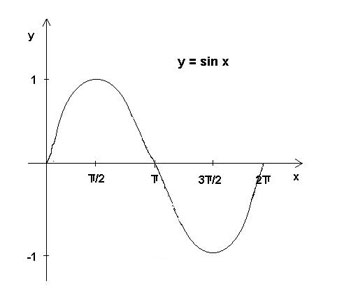
Итак, в прямоугольном треугольнике отношение длин двух сторон не зависит от их длины ,а зависит лишь от величины острого угла. Было бы непростительно оставить этот факт без внимания, поэтому указанным отношениям дали названия синус, косинус, тангенс. Историческая справкаВ IV-V веках появился уже специальный термин в трудах по астрономии великого индийского учёного Ариабхаты, именем которого назван первый индийский спутник Земли. Дугу он назвал ардхаджива (ардха – половина, джива – тетива лука, которую напоминает хорда). Позднее появилось более краткое название джива. Арабскими математиками в IX веке это слово было заменено на арабское слово джайб (выпуклость). При переводе арабских математических текстов в веке оно было заменено латинским синус (sinus – изгиб, кривизна). Вид функции синус
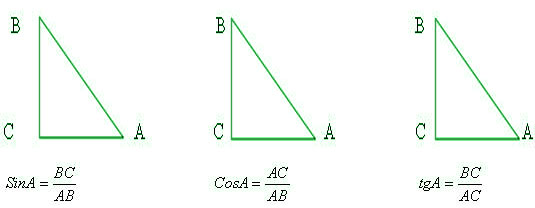
Понятия «противоположный катет» и «прилежащий катет»Для угла А катет ВС-противолежащий, а АС-прилежащий. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами. Катет — одна из двух сторон прямоугольного треугольника, образующих прямой угол. Противоположная прямому углу сторона называется гипотенузой. Для непрямоугольного треугольника катеты не существуют. Название «катет» происходит от греческого kathetos — перпендикуляр, опущенный, отвесный. Название также встречается в архитектуре и означает отвес через средину задка ионической капители. a, b - катеты
Синус острого угла прямоугольного треугольника равен отношению противолежащего к данному острому углу катета и гипотенузы. Косинус острого угла прямоугольного треугольника равен отношению прилежащего к данному острому углу катета и гипотенузы. Тангенс острого угла прямоугольного треугольника равен отношению противолежащего к данному острому углу катета к прилежащему. Котангенс острого угла прямоугольного треугольника равен отношению прилежащего к данному острому углу катета к противолежащему.
Рассмотрим функцию тангенс подробнее. Рассмотрим соотношения выплывающие с основных. Катет прямоугольного треугольника равен: Катет прямоугольного треугольника равен произведению: гипотенузы и синуса противолежащего угла; гипотенузы и косинуса прилежащего угла; другого катета и тангенса противолежащего угла; другого катета и котангенса прилежащего угла. Гипотенуза прямоугольного треугольника равна: Гипотенуза прямоугольного треугольника равна отношению: катета и синуса, противолежащего этому катету угла; катета и косинуса, прилежащего этому катету угла (не зависимо от того, какой катет известен).
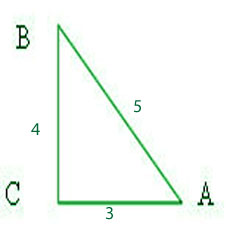
Практическая частьЗадание №1Какое отношение верно?
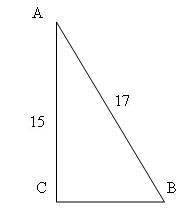
Задание №2В прямоугольном треугольнике гипотенуза равна 15 см, а синус одного из острых углов равен 0,6. Чему равен катет, противолежащий данному острому углу?
Задание №3Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то эта сторона лежит против:
Интересный фактРазвитие тригонометрии. Долгое время тригонометрия носила чисто геометрический характер, т. е. Факты, которые мы сейчас формулируем в терминах тригонометрических функций, формулировались и доказывались с помощью геометрических понятий и утверждений. Такою она была еще в средние века, хотя иногда в ней использовались и аналитические методы, особенно после появления логарифмов. Пожалуй, наибольшие стимулы к развитию тригонометрии возникали в связи с решением задач астрономии, что представляло большой практический интерес (например, для решения задач определения местонахождения судна, предсказания затемнения и т. д.). Астрономов интересовали соотношения между сторонами и углами сферических треугольников. И надо заметить, что математики древности удачно справлялись с поставленными задачами.
Вопросы
Список использованных источников
Потурнак С.А. Жизнякова Зоя Стапановна Шишкова Елена Николаевна Парфенова Елена Витальевна
|
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: