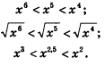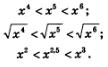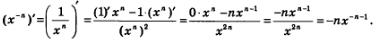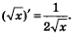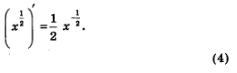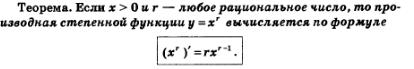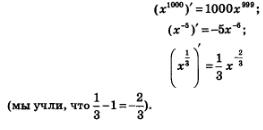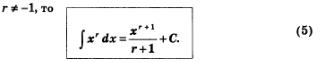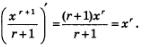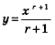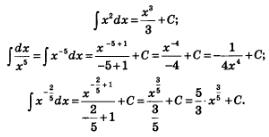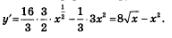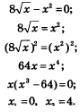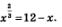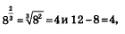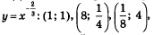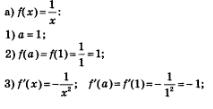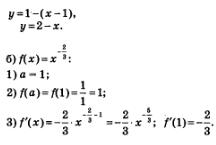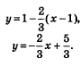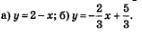|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Степенные функции, их свойства и графики
§ 44. Степенные функции, их свойства и графики
Обычно степенными функциями называют функции вида у = хr, где r-любое действительное число. В этом параграфе мы ограничимся случаями рационального показателя r.
Целый ряд таких функций мы с вами уже изучили. Так, если r— натуральное число (r = п), то получаем функцию у = хп; графики и свойства таких функций вам известны из курса алгебры 7—9-го классов. На рис. 180 изображен график функции у =х1 (прямая), на рис. 181 изображен график функции у =хг (парабола), на рис. 182 изображен график функции у =х3 (кубическая парабола). График
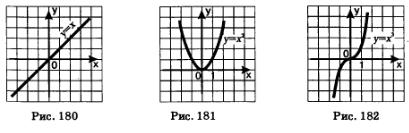
степенной функции у = хп в случае четного п (п =4, 6, 8, ...) похож на параболу, а график степенной функции у = х" в случае нечетного п(п= 5, 7, 9,...) похож на кубическую параболу.
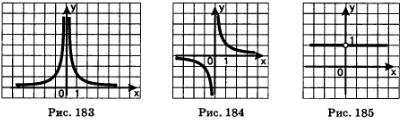
Если г = -п, то получаем функцию 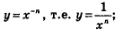 о таких функциях мы говорили в курсе алгебры 9-го класса. В случае четного п график имеет вид, изображенный на рис. 183; в случае нечетного п график имеет вид, изображенный на рис. 184. о таких функциях мы говорили в курсе алгебры 9-го класса. В случае четного п график имеет вид, изображенный на рис. 183; в случае нечетного п график имеет вид, изображенный на рис. 184.
Наконец, если г=0, т.е. речь идет о функции у=х°, то о ней и говорить неинтересно, поскольку это — функция у = 1, где 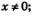 ; график этой функции изображен на рис. 185. ; график этой функции изображен на рис. 185.
Теперь познакомимся с функциями у = хг, где г положительное или отрицательное дробное число.
Рассмотрим в качестве примера функцию y=x2,5. Область ее определения — луч 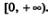 Построим на этом луче графики функций у = х2 (ветвь параболы) и у=х3 (ветвь кубической параболы) — эти графики изображены на рис. 186. Обратите внимание: на интервале (0, 1) кубическая парабола располагается ниже, а на открытом луче Построим на этом луче графики функций у = х2 (ветвь параболы) и у=х3 (ветвь кубической параболы) — эти графики изображены на рис. 186. Обратите внимание: на интервале (0, 1) кубическая парабола располагается ниже, а на открытом луче 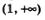 выше параболы. выше параболы.
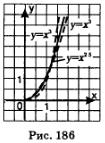
Нетрудно убедиться в том, что график функции у =х2,5, проходит через точки (0; 0) и (1; 1), как и графики функций у = х2, у = х3. При остальных значениях аргумента х график функции у=х2,5 находится между графиками функций у=х2 и у=х3 (рис. 186). Почему? Смотрите:
1) Если О<х< 1, то:
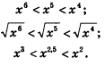
2) Если х> 1, то:
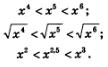
Примерно так же обстоит дело для любой степенной функции вида 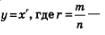 неправильная дробь (числитель больше знаменателя). Ее графиком является кривая, похожая на ветвь параболы. Чем больше показатель г, тем «круче» устремлена эта кривая вверх. неправильная дробь (числитель больше знаменателя). Ее графиком является кривая, похожая на ветвь параболы. Чем больше показатель г, тем «круче» устремлена эта кривая вверх.
Свойства функции 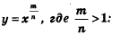
1) 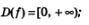
2) не является ни четной, ни нечетной;
3) возрастает на 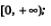
4) не ограничена сверху, ограничена снизу;
5) не имеет наибольшего значения; 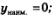
6) непрерывна;
7) 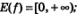
8) выпукла вниз.
Рассмотрим степенную функцию 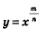 для случая, когда для случая, когда 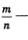 правильная дробь правильная дробь 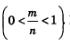
Все рассмотренное в § 40 в отношении функции 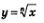 или, что то же самое, или, что то же самое, 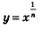 (ее график изображен на рис. 169) имеет место и по отношению к любой степенной функции вида (ее график изображен на рис. 169) имеет место и по отношению к любой степенной функции вида 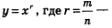 правильная дробь (числитель меньше знаменателя). График функции у = хг изображен на рис. 187. правильная дробь (числитель меньше знаменателя). График функции у = хг изображен на рис. 187.
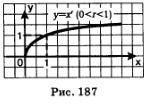
Свойства функции 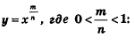
1) 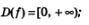
2) не является ни четной, ни нечетной;
3) возрастает на 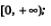
4) не ограничена сверху, ограничена снизу;
5) не имеет наибольшего значения; 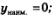
6) непрерывна;
7) 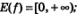
8) выпукла вверх.
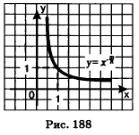
Нам осталось рассмотреть степенную функцию вида 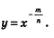 Область ее определения — открытый луч (0, + оо). Выше мы построили график степенной функции у = х-n, где п — натуральное число. При х > 0 график функции у =х-п пoхож на ветвь гиперболы (рис. 184). Точно так же обстоит дело для любой степенной функции вида Область ее определения — открытый луч (0, + оо). Выше мы построили график степенной функции у = х-n, где п — натуральное число. При х > 0 график функции у =х-п пoхож на ветвь гиперболы (рис. 184). Точно так же обстоит дело для любой степенной функции вида 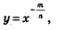 , график которой изображен на рис. 188. Отметим, что график данной функции имеет горизонтальную асимптоту у = 0 и вертикальную асимптоту х = 0. , график которой изображен на рис. 188. Отметим, что график данной функции имеет горизонтальную асимптоту у = 0 и вертикальную асимптоту х = 0.
Свойства функции 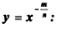
1) 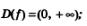
2) не является ни четной, ни нечетной;
3) убывает на (0, + оо);
4) не ограничена сверху, ограничена снизу;
5) не имеет ни наибольшего, ни наименьшего значения;
6) непрерывна;
7) 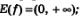
8) выпукла вниз.
Вы заметили, наверное, что мы пока ничего не сказали о свойстве дифференцируемости степенной функции. Начнем издалека.
Мы знаем, чему равна производная функции у =хn, где п — натуральное число:

Нетрудно найти производную степенной функции у = х-n, где n — натуральное число. Для этого надо переписать выражение х-n в виде 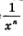 и воспользоваться правилом дифференцирования дроби: и воспользоваться правилом дифференцирования дроби:
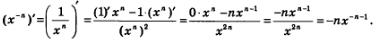
Итак, для любого 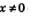 справедлива формула справедлива формула

Формулы (1) и (2) можно объединить в одну:

где m — любое целое число.
Идем дальше. Мы знаем, что 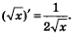 Эту формулу можно записать следующим образом: Эту формулу можно записать следующим образом:
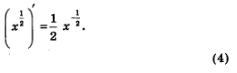
И формула (3), и формула (4) являются частными случаями общего утверждения (которое мы приводим без доказательства).
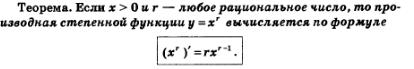
Например,
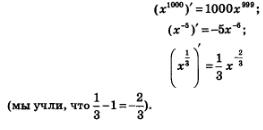
Нетрудно получить и соответствующую формулу для интегрирования степенной функции: если
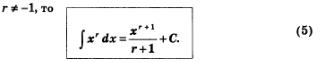
В самом деле, 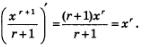
Значит, функция 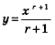 является первообразной для функции у = хг, а потому справедлива формула (5). Например, является первообразной для функции у = хг, а потому справедлива формула (5). Например,
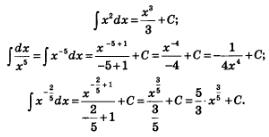
Рассмотрим ряд примеров.
Пример 1. Найти наибольшее и наименьшее значения функции 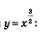 на отрезке [1, 9]; б) на интервале (0, 4); в) на луче на отрезке [1, 9]; б) на интервале (0, 4); в) на луче 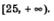
Решение. Нам нет необходимости строить график функции, можно воспользоваться тем, что она возрастает и, следовательно, свое наименьшее и наибольшее значения достигает соответственно в левом и правом концах заданного промежутка, если, разумеется, концы промежутка принадлежат самому промежутку.
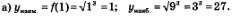
б) Здесь нет ни наименьшего, ни наибольшего значения функции, поскольку концы промежутка — точки 0 и 4 — интервалу (0, 4) не принадлежат.
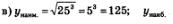 не существует. не существует.
Пример 2. Найти наибольшее и наименьшее значения функции
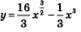 на отрезке [1, 9]. на отрезке [1, 9].
Решение. Воспользуемся алгоритмом отыскания наибольшего и наименьшего значений непрерывной функции на отрезке (см. § 36).
1) Имеем 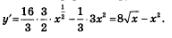
2) Производная существует при всех х, значит, критических точек у функции нет, а стационарные найдем из условия у'=0. Имеем:
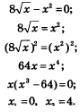
Отрезку [1,9] принадлежит лишь точка х = 4.
3) Составим таблицу значений функции 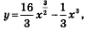 включив в нее концы отрезка — точки x = 1 и x = 9 — и найденную стационарную точку х = 4: включив в нее концы отрезка — точки x = 1 и x = 9 — и найденную стационарную точку х = 4:

Таким образом,

Пример 3. Решить уравнение 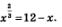
Решение. Нетрудно подобрать один корень этого уравнения: х = 8. В самом деле,
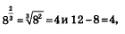
значит, при х=4 уравнение обращается в верное числовое равенство 4=4.
Так как степенная функция 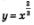 возрастает, а линейная функция у = 12 - х убывает, то других корней у уравнения нет. возрастает, а линейная функция у = 12 - х убывает, то других корней у уравнения нет.
Ответ: х = 8.
Пример 4. Построить график функции
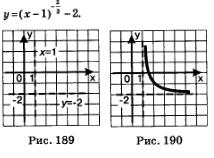
Решение. 1) Перейдем к вспомогательной системе координат с началом в точке (1; -2) — пунктирные прямые x = 1 и у = -2на рис. 189.
2) «Привяжем» функцию 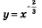 к новой системе координат. Для этого выберем контрольные точки для функций к новой системе координат. Для этого выберем контрольные точки для функций 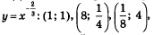
но строить их будем не в старой, а в новой системе координат. Затем по этим точкам построим кривую того вида, какой представлен на рис. 188. Это и будет требуемый график (рис. 190).
Пример 5. Составить уравнение касательной к 1 -графику функции: 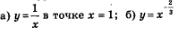 в точке х = 1. в точке х = 1.
Решение. Напомним общий вид уравнения касательной:
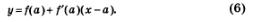
Воспользуемся алгоритмом составления уравнения касательной (см. § 34).
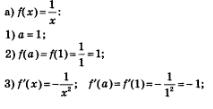
4) Подставим найденные три числа: 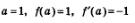 в формулу (6). Получим: в формулу (6). Получим:
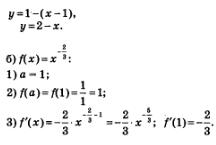
4) Подставим найденные три числа: 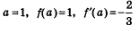 вформулу (6). Получим: вформулу (6). Получим:
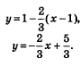
Ответ: 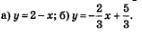
Замечание. График функции 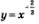 похож на ветвь гиперболы похож на ветвь гиперболы 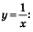 оба графика имеют своими асимптотами оси координат, оба графика проходят через точку (1; 1). Но их поведение в точке (1; 1) различное, у них, как мы увидели при решении примера 5, разные касательные в этой точке (см. рис. 191,192). оба графика имеют своими асимптотами оси координат, оба графика проходят через точку (1; 1). Но их поведение в точке (1; 1) различное, у них, как мы увидели при решении примера 5, разные касательные в этой точке (см. рис. 191,192).
Пример 6. Найти площадь фигуры, ограниченной линиями
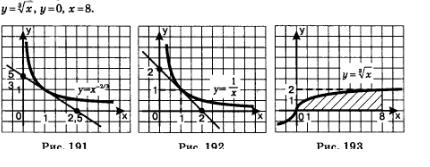
Решение. Фигура, площадь которой требуется вычислить, изображена на рис. 193. Имеем (см. § 38):

Ответ: S = 12.
А.Г. Мордкович Алгебра 10 класс
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|