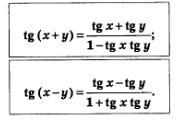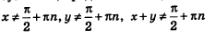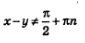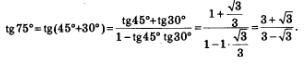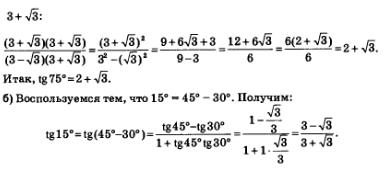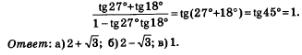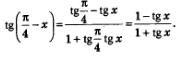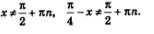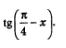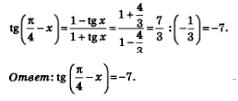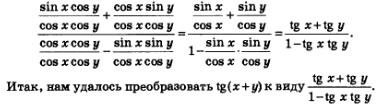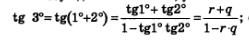|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Тангенс суммы и разности аргументов
§ 23. Тангенс суммы и разности аргументов
В § 21 и 22 мы получили формулы, выражающие синус и косинус суммы и разности аргументов через синусы и косинусы аргументов. В этом параграфе речь пойдет о том, как тангенс суммы или разности аргументов выражается через тангенсы аргументов. Соответствующие формулы выглядят следующим образом:
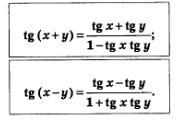
При этом, разумеется, предполагается, что все тангенсы имеют смысл, т.е. что 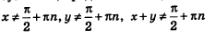 (для первой формулы), (для первой формулы), 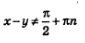 (для второй формулы). (для второй формулы).
Доказательства этих формул достаточно сложны, мы приведем одно из них в конце параграфа. Но сначала рассмотрим ряд примеров, показывающих, как используются эти формулы на практике.
Пример 1. Вычислить: 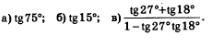
Решение, а) Воспользуемся тем, что 75° = 45° + 30°. Получим:
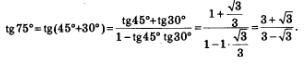
Есть смысл избавиться от иррациональности в знаменателе, домножив и числитель, и знаменатель полученной дроби на
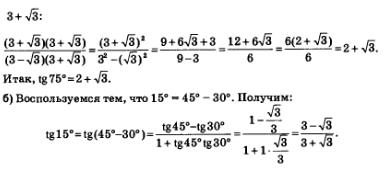
Есть смысл избавиться от иррациональности в знаменателе, домножив и числитель, и знаменатель полученной дроби на
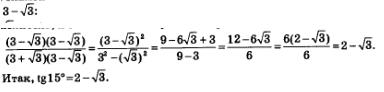
в) Заметим, что заданное выражение представляет собой правую часть формулы «тангенс суммы» для аргументов 27° и 18°. Значит,
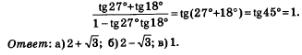
Пример 2. Доказать тождество: 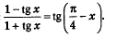
Решение. Применим к правой части проверяемого тождества формулу «тангенс разности». Имеем:
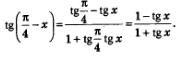
Замечание. Когда речь идет о доказательстве тригонометрического тождества или о преобразовании тригонометрического выражения, всегда предполагается, что аргументы принимают только допустимые значения. Так, в рассмотренном примере доказанное тождество справедливо при условии, что 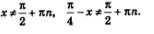
Пример 3. Вычислить 
Решение. Воспользуемся тождеством, полученным в предыдущем примере:

Если мы вычислим tg х, то вычислим и 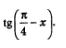
Значение соs x; задано, значение tg х найдем с помощью соотношения

По условию аргумент x принадлежит второй четверти, а в ней тангенс отрицателен. Поэтому из равенства 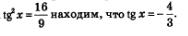
Подставим найденное значение в правую часть формулы (1):
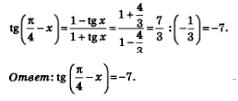
В заключение докажем, как было обещано, формулу тангенса суммы. Кроме того, приведем довольно любопытный пример, показывающий неожиданное применение формулы тангенса суммы.
Имеем:
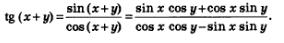
Разделим в полученной дроби и числитель, и знаменатель почленно на соs х соз у. Получим:
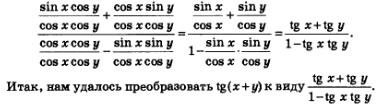
Пример 4. Доказать, что 1° — иррациональное число.
Решение. Предположим противное, что tg 1°— рациональное число :tg 1 °=r, где г — рациональное число. Имеем:
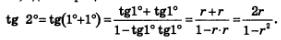
Получилось рациональное число, обозначим его q; итак tg 2°=q.
Рассуждая аналогично, устанавливаем, что: 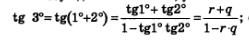 снова получили рациональное число. Продолжая процесс, получим, что 4°, 5°, 60° — рациональные числа. Но снова получили рациональное число. Продолжая процесс, получим, что 4°, 5°, 60° — рациональные числа. Но 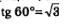 а это — иррациональное число. Получили противоречие, значит, сделанное предположение неверно, т.е. tg 1° — иррациональное число. а это — иррациональное число. Получили противоречие, значит, сделанное предположение неверно, т.е. tg 1° — иррациональное число.
А.Г. Мордкович Алгебра 10 класс
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|