|
Гипермаркет знаний>>Математика>>Математика 8 класс. Полные уроки>>Геометрия: Теорема Пифагора. Полные уроки
Тема урокаТеорема Пифагора Цели урока• Познакомиться школьников с теоремой Пифагора; Задачи урока• Научиться использовать свойства фигур при выполнении заданий. План урока• Краткие биографические сведения. Краткие биографические сведения о ПифагореНа жаль, Пифагор не оставил никаких сочинений о своей биографии, поэтому все сведения об этом великом философе и знаменитом математике мы можем узнать только благодаря воспоминаниям его последователей, да и то не всегда справедливых. Поэтому об этом человеке ходит много легенд. Но правда заключается в том, что Пифагор был великим эллинским мудрецом, философом и талантливым математиком. По недостоверным сведениям, великий мудрец и гениальный ученый Пифагор родился в далеко не бедной семье, на острове Самосее, приблизительно в 570 году до н.э. Появление на свет гениального ребенка предрекла Пафия. Поэтому будущий светила получил свое имя Пифагор, которое обозначает, что это именно тот, о ком объявила Пафия. Она предсказала, что рожденный младенец в будущем принесет немало пользы и добра людям. Новорожденный был безумно красив, а современем порадовал окружающих своими выдающимися способностями. А так как юное дарование коротало свои дни среди мудрых старцев, то в будущем это принесло свои плоды. Вот так благодаря Гермодаманту Пифагор полюбил музыку, а Ферекид направил ум ребенка к логосу. После жизни в Самосее Пифагор отпправился в Милеет, где произошло знакомство еще с одним ученым - Фалесом. Пифагор познакомился со знаниями всех известных по тем временам мудрецов, так как был допущен к обучению и познанию всех таинств, которые были другим запрещены. Он старался докопаться до истины и впитать все накопленные человечеством знания. После двадцати двух лет пребывания в Египте, Пифагор перебрался в Вавилон, где продолжил свое общение с различными мудрецами и магами. Вернувшись в конце своей жизни в Самиос, он был признан одним из мудрейших людей того времени. Теорема ПифагораДаже человек, которому пока не довелось изучать эту теорему, наверняка слышал высказывание о «пифагоровых штанах». Особенность этой теоремы в том, что она стала одной из ключевых теорем евклидовой геометрии. Она позволяет легко найти и установить соответствие между сторонами прямоугольного треугольника. Теорема Пифагора запомнилась каждому школьнику не только высказыванием: «пифагоровы штаны на все стороны равны», а своей простотой и значимостью. И на первый взгляд эта теорема хотя и кажется простой, но имеет большое значение, так как в геометрии она применяется фактически на каждом шагу.
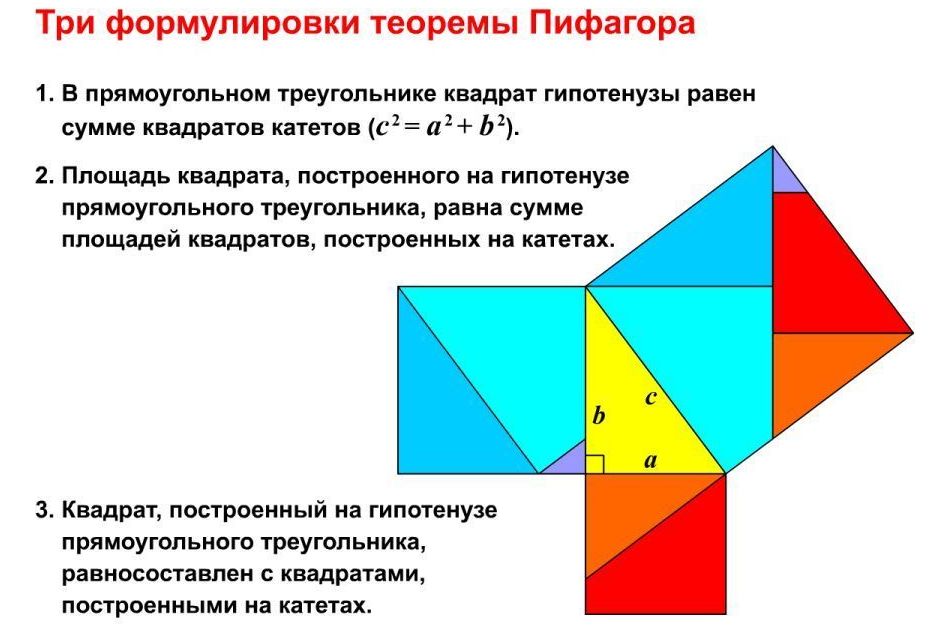
Теорема Пифагора насчитывает большое количество разных доказательств и, наверное, является единственной теоремой, которая имеет такое огромное число доказательств. Такое разнообразие подчеркивает безграничную значимость этой теоремы В теореме Пифагора присутствуют геометрические, алгебраические, механические и другие доказательства. Об открытии теоремы Пифагором сложено много разных легенд. Но, несмотря на все это, имя Пифагора навеки вошло в историю геометрии и прочно слилось с теоремой Пифагора. Ведь этот гениальный математик первым представит доказательство теоремы, которая носит его имя. Формулировки теоремыСуществуют несколько формулировок теоремы Пифагора. Евклидова теорема говорит нам, что квадрат стороны прямоугольного треугольника, проведенный над его прямым углом, равняется квадратам на сторонах, заключающих прямой угол.
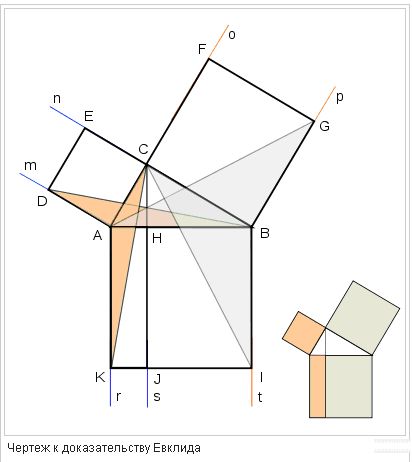
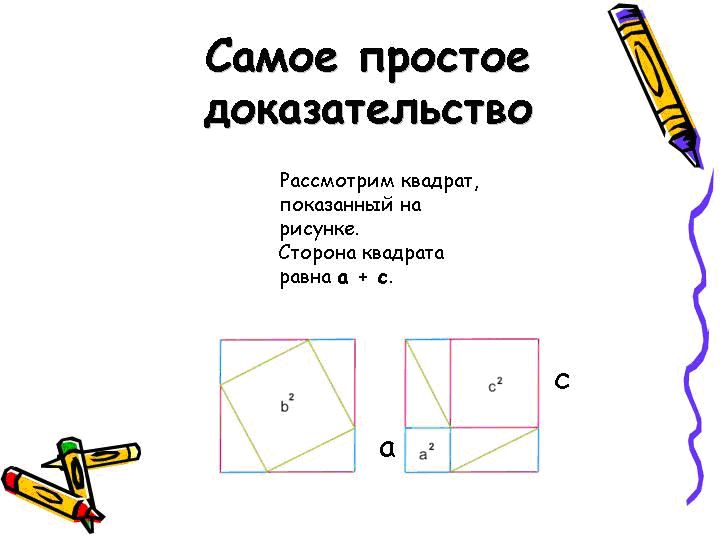
Задание: Найдите различные формулировки теоремы Пифагора. Находите ли вы в них какое-то различие? Упрощенное доказательство ЕвклидаНезависимо от того, мы берем метод разложения или доказательство Евклида, можно использовать любое расположение квадратов. В некоторых случаях при этом можно достичь небольших упрощений. Возьмем квадрат, который построен на одном из катетов и имеет тоже расположение, что и треугольник. Мы видим, что продолжение стороны, противоположной катету этого квадрата проходит через вершину квадрата, который построен на гипотенузе. Доказательство теоремы выглядит довольно просто, так как будет достаточно просто сравнить площади фигур с площадью треугольника. И мы видим, что S треугольника равна ½ площади квадрата, а также ½ S прямоугольника. Самое простое доказательствоАлгебраическое доказательствоК алгебраическому доказательству теоремы Пифагора относятся элементарные методы, которые присутствуют в алгебре. Это способы решения уравнений в сочетании со способом замены переменных. Давайте рассмотрим это доказательство более детально. И так, у нас есть прямоугольник АВС, у которого прямой угол – С. Проведите с этого угла высоту CD. Согласно определения косинуса угла мы получим: соsА=AD/AC=AC/AB. Отсюда AB*AD=AC2. И соответственно: соsВ = BD/BC=BC/AB. Отсюда AB*BD=ВС2. Теперь сложим эти равенства почленно и увидим, что: AD+DB=AB, В итоге: АС2+ВС2=АВ(AD + DB)=АВ2. Вот и все, теорема доказана. Интересный фактТеорему Пифагора ученые «доказали» с помощью мультиков. Группа единомышленников из института им. Стеклова получила премию за оригинальный математический проект, который они разработали для школьников и учителей. Они создали мини уроки по математике, которые этот скучный предмет превратили в очень интересный и познавательный. Свои необычные этюды молодые ученые выпустили на дисках и выложили в Интернете на всеобщее обозрение.
Вопросы 1. Кто такой Пифагор? Задачи с применением теоремы ПифагораИспользуя знания теоремы Пифагора, попробуйте решить следующие задачи: • Из туристической базы, одновременно, вышли две группы туристов. Первая группа пошла на юг и прошла семь километров, а вторая свернула на запад и прошла девять километров. Используя знания теоремы, найдите расстояние между группами туристов. • Если в прямоугольном треугольнике его катет равен 15 см, а гипотенуза равняется 16 см, то чему будет равен второй катет? • Чему будет равна площадь трапеции, когда ее большое основание равно 24 см, меньшее – 16, а большая диагональ прямоугольной трапеции равна 26 см? Домашнее заданиеОформите в виде небольшого доклада несколько доказательств теоремы Пифагора, которые вам понятны и решите задачи. 1. Найдите диагональ прямоугольного треугольника, при условии, что стороны его равны 8 см и 32 см. 2. Найдите медиану треугольника, которая проведена к основанию, если в равнобедренном треугольнике периметр равен 38 см, а его боковая сторона равняется 15 см. 3. У треугольника стороны равны 10см, 6 см и 9 см. Попробуйте определить, является ли этот треугольник прямоугольным? |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: