|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Третий признак равенства треугольников. Полные уроки ТЕМА УРОКА: Третий признак равенства треугольников. Цели урока:
План урока:
Из истории математики. Термин катет происходит от греческого слова «катетос », которое означало отвес , перпендикуляр. В средние века словом катет означали высоту прямоугольного треугольника, в то время, как другие его стороны называли гипотенузой, соответственно основанием. В XVII веке слово катет начинает применяться в современном смысле и широко распространяется, начиная с XVIII века. Евклид употребляет выражения: «стороны, заключающие прямой угол», - для катетов; «сторона, стягивающая прямой угол», - для гипотенузы. Для начала нам необходимо освежить в памяти предыдущие признаки равенства треугольников. И так начнем с первого. 1-ый признак равенства треугольников. Файл:T.gifТеорема. Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Доказательство: Так как ∠А=∠А1 ( по условию), то треугольник АВС можно наложить на треугольник А1В1С1, так что вершина А совместится с вершиной А 1 , а стороны АВ и АС наложатся соответственно на лучи А1В1 и А1С1. Поскольку АВ = А1В1, АС = А1С1, то сторона АВ совместится со стороной А1В1, а сторона - АС состороной А1С1; в частности совместятся точки В и В1, С и С1. Следовательно, совместятся стороны ВС и В1С1. Итак, ∆АВС и ∆А1В1С1 полностью совместятся, значит они равны.
2-ой признак равенства треугольников. Файл:T.gifТеорема. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство: Пусть A1B1C1 – треугольник, равный треугольнику ABC. Так как AB = A1B1, то вершина B совпадает с вершиной B1. Так как ∠ A = ∠ A1 и ∠ B = ∠ B1, то луч A1C1 совпадает с лучом AC, а луч B1C1 совпадает с лучом BC. Отсюда следует, что вершина С совпадает с вершиной С1. Треугольник A1B1C1 совпадает с треугольником ABC, а значит, равен треугольнику ABC. Теорема доказана.
3-ий признак равенства треугольников. Файл:T.gifТеорема.
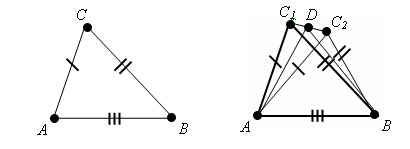
Доказательство: Пусть треугольники ABC и A1B1C1 такие, что AB=A1B1, AC=A1C1, BC=B1C1. Требуется доказать, что треугольники равны. Допустим, что треугольники не равны. Тогда ∠ A ≠ ∠ A1, ∠ B ≠ ∠ B1, ∠ C ≠ ∠ C1 одновременно. Иначе треугольники были бы равны по первому признаку. Пусть треугольник A1B1C2 – треугольник, равный треугольнику ABC, у которого вершина С2 лежит в одной полуплоскости с вершиной С1 относительно прямой A1B1. Пусть D – середина отрезка С1С2. треугольники A1C1C2 и B1C1C2 равнобедренные с общим основанием С1С2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой С1С2. Прямые A1D и B1D не совпадают, так как точки A1, B1, D не лежат на одной прямой. Но через точку D прямой С1С2 можно провести только одну перпендикулярную ей прямую. Мы пришли к противоречию. Теорема доказана.
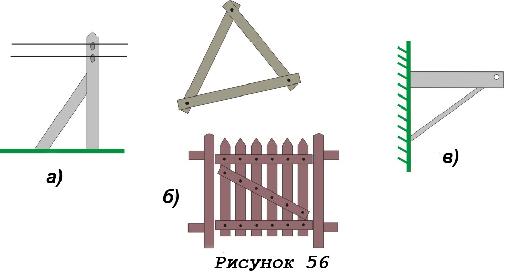
Из третьего признака равенства треугольников следует, что треугольник – жесткая фигура. Это свойство – жесткость треугольника широко используется на практике. Так, чтобы закрепить столб в вертикальном положении, к нему ставят подпорку (Рис. 56, а); такой принцип используется на заборах во дворе (Рис. 56, б), при установке кронштейна (Рис. 56, в).
Актуализация опорных знаний. На секунду отвлечемся от признаков равенства треугольников и проведем маленький тест. Проверим правильность написания геометрических терминов.
(Острый)
(Продлить одну из сторон).
(Смежными, потому что у них одна сторона общая, а две другие являются продолжением одна другой.)
( Сумма смежных углов равна 180°.)
(Продолжить обе стороны).
( Если стороны одного угла являются продолжением сторон другого).
(Вертикальные углы равны).
(Две геометрические фигуры называются равными, если их можно совместить наложением).
Оказывается, что такая возможность есть и для этого необязательно накладывать одну фигуру на другую. Для этого достаточно сравнить некоторые элементы треугольников.
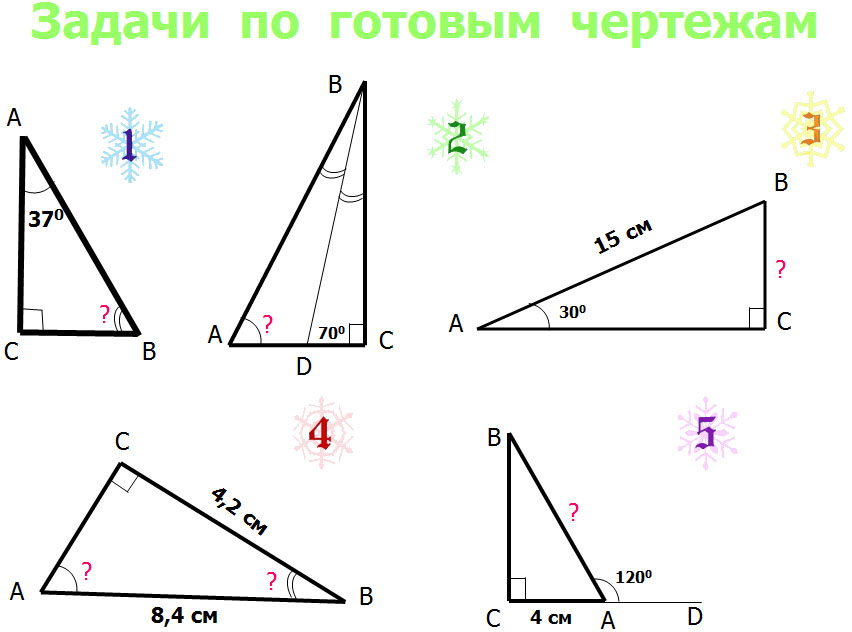
В признаках о равенстве треугольников присутствуют отдельно признаки равенства прямоугольных треугольников. Признаки равенства прямоугольных треугольников. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Интересный факт: О пирамидах По мнению учёных, слово "Пирамида" произошло от названия пирога пирамидальной формы. Доктор Карл Бенедикс был первым из известных нам ученых, кто провел эксперимент с пирамидами. Хорошо известно применение пирамид в целительстве и медитации. По числу углов основания различают пирамиды треугольные, четырёхугольные и т.д. Слово «пирамида» — греческое. Пирамиды представляют собой огромные каменные сооружения пирамидальной формы. ЭHЕРГИЯ ПИРАМИД Величайшим и самым загадочным из семи чудес древнего мира является комплекс пирамид Гизы в Египте, наиболее впечатляющей из которых является пирамида Хеопса. Ученые и теологи уже многие столетия изучают Великую Пирамиду, поражаясь величию совершенного гигантского труда по ее созданию, удивляясь той острейшей и глубинной необходимости, которая подвигнула на такой геркулесов труд. О пирамиде Хеопса говорят как о наиболее совершенном сооружении в мире, эталоне мер и весов, о том, что в ее геометрической форме закодирована информация о строении Вселенной, Солнечной системы и человека. Hо утверждениям известного ясновидца Э.Кейси в Великой Пирамиде хранятся летописи и предметы атлантов, доказываю щие существование высокоразвитой науки и технологии в далеком прошлом, а сама Пирамида была построена между 10490 и 10390 годами до нашей эры. Египтологи, впрочем, считают, что большие гизские пирамиды Хеопса, Хефрена и Микерина, имеющие классическую пирамидальную форму, возведены в период Древнего царства при 1V династии фараонов, то есть примерно 2800-2250 гг. до н.э. Отправным пунктом большинства существующих гипотез о функциональном назначении Великой Пирамиды - быть усыпальницей фараона, противостоит мнение об ином, скрытом от непосвященных предназначении. ЭЗОТЕРИКА ПИРАМИД Слово пирамида происходит от греческого "пирамис", эти-мологически связанного с "пир" - "огонь", обозначая символическое представление Единого Божественного Пламени, жизни всех созданий. Посвященные прошлого считали пирамиду идеальным символом Тайной Доктрины - символом иерархии, существующей во Вселенной. Квадратное основание пирамиды обозначает землю, четыре его стороны - четыре элемента материи или субстанции, из комбинации которых создана материальная природа. Треугольные стороны ориентированы в направлении четырех сторон света, что символизирует противоположности тепла и холода (юг и север), света и тьмы (восток и запад). Поднимающиеся от каждой стороны основания треугольники вершиной вверх, служат символом Божественного существа, Духа, заключенного в четырехмерную материальную природу. Сумма сторон основания равна четырем, что соответствует материи, треугольников - трем, что соотносится с Духом. Сумма сторон основания и треугольника составляет семь, символизируя совершенного человека, выражающего свою Истинную Природу, заключающуюся в объединении духа и плоти. Голова человека символизируется тройкой, треугольником, а четыре конечности - четверкой, причем расположение тройки над четверкой означает доминирование духа над материей. Сумма сторон четырех поверхностей пирамиды составляет двенадцать, что соответствует двенадцати знакам зодиака. Три главных камеры пирамиды соотносятся с мозгом, сердцем и воспроизводящей системой человека, а также с тремя главными его энергетическими центрами. Основное назначение Великой Пирамиды тщательно скрывалось. Она не была ни гробницей фараона, ни обсерваторией, а являлась гигантским, мощнейшим генератором особой энергии, используемой фараоном и жрецами для различных целей. Согласно эзотерической доктрине Великая Пирамида была первым храмом Мистерий, Хранилищем секретных истин, лежащих в основе всех искусств и наук, всего мироздания. Техника и ритуал Мистерий были созданы мифическим Мастером Скрытого Дома, обитавшем в Великой Пирамиде невидимо для всех, кроме обладавших вторым зрением. Мистерии учат, что Божественная энергия нисходит на вер шину пирамиды, из которой она распространяется по наклонным сторонам, растекаясь по миру. Венчающий пирамиду камень, отсутствующий в настоящее время, представлял, вероятно, миниатюрную пирамиду, повторяющую всю структуру основной. Таким образом Великая Пирамида уподоблялась Вселенной, а венчающий камень - человеку. Вопросы:
Список использованных источников:
Отредактировано и выслано Потурнаком С. А. Над уроком работали Потурнак С. А. Кулешовая Г. Н. Марина Александровна Самылина М. В.
Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, но и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: