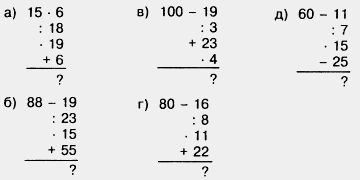|
Гипермаркет знаний>>Математика>>Математика 5 класс>>Математика:Уравнение
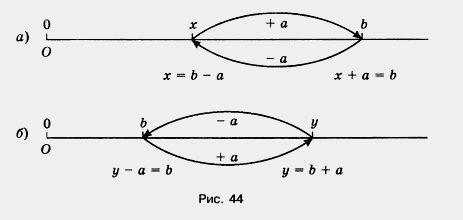
Задача. На левой чашке весов лежат арбуз и гиря в 2 кг, а на правой чашке — гиря в 5 кг. Весы находятся в равновесии. Чему равна масса арбуза? Решение. Обозначим неизвестную массу арбуза буквой х. Так как весы находятся в равновесии, должно выполняться равенство х + 2 = 5. Нам надо найти такое значение х, при котором выполняется это равенство. По смыслу вычитания, таким значением будет разность чисел 5 и 2, то есть 3. Значит, масса арбуза равна 3 кг. Пишут: х = 3. Если в равенство входит буква, то равенство может быть верным при « одних значениях этой буквы и неверным при других ее значениях. Например, равенство х + 2 = 5 верно при х = 3 и неверно при х = 4. Уравнением называют равенство, содержащее букву, значение которой надо найти. Значение буквы, при котором из уравнения получается верное числовое равенство, называют корнем уравнения. Решить уравнение — значит найти все его корни (или убедиться, что это уравнение не имеет ни одного корня). Пример 1. Решим уравнение х + 12 = 78. Решение. По смыслу вычитания, неизвестное слагаемое равно разности суммы и другого слагаемого.
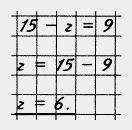
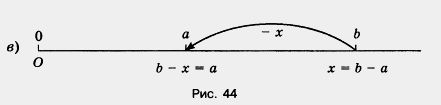
Число 6 является корнем уравнения 15 - z = 9, так как верно равенство 15-6 = 9. Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность (рис. 44, в).
а) x + 37 = 85;
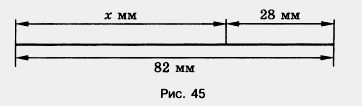
а) В корзине было несколько грибов. После того как в нее положили еще 27 грибов, их стало 75. Сколько грибов было в корзине? 374. Составьте уравнение по рисунку 45 и решите его.
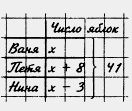
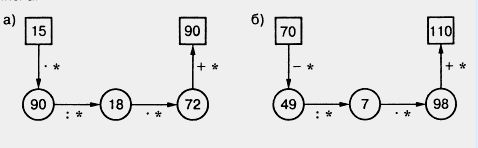
1) сначала найти неизвестное уменьшаемое y + 64= 48 + 38, у + 64 = 86, а потом найти неизвестное слагаемое у: у = 86 - 64, у = 22, или 2) сначала упростить выражение, стоящее в левой части уравнения, использовав свойства вычитания: Подобным образом решите двумя способами уравнение: а) (х + 98) + 14 = 169; б) (35 + у) - 15 = 31. 376. Решите уравнение и выполните проверку: а) (х + 15) - 8 - 17; г) (у - 35) + 12 = 32; 377. Решите с помощью уравнения задачу: а) Витя задумал число. Если к этому числу прибавить 23 и к полученной сумме прибавить 18, то получится 52. Какое число задумал Витя? 378. Запишите в виде равенства: а) У Вани было х яблок, у Пети — на 8 яблок больше, а у Нины — на 3 яблока меньше, чем у Вани. Вместе у них было 41 яблоко. 379. Сумма 3986 + 5718 равна 9704. Пользуясь этим, найдите без вычислений значение выражения или корень уравнения: а) 9704 - 3986; г) 3986 + у = 9704; 380. Разность 6877 - 2984 равна 3893. Пользуясь этим, найдите без вычислений значение выражения или решите уравнение: а) 2984 + 3893; в) х - 3893 = 2984; 381. Вместо звездочек в записи вычислений цепочкой поставьте необходимые числа.
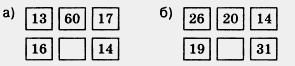
а) левее точки Е и на сколько единичных отрезков; 384. Что больше и во сколько раз: а) два часа или сорок минут; 385. В бидоне 24 л молока. Для приготовления завтраков израсходовали четвертую часть молока, а для приготовления обедов — половину оставшегося молока. Сколько литров молока осталось в бидоне? 386. Найдите пропущенное число:
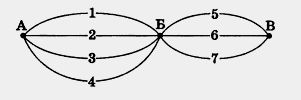
388. Из села Аникеево в село Большово ведут четыре дороги, а из села Большово в село Виноградово — три дороги. Сколькими способами можно добраться из Аникеева в Виноградово через село Большово?
Точно так же рассуждая, получаем по три способа продолжить путь, начав добираться и по 2-й, и по 3-й, и по 4-й дороге. Значит, всего получается4 • 3 = 12 способов добраться из Аникеева в Виноградово. Немецкого ученого Кaрла Гaусса называли королем математиков. Его математическое дарование проявилось уже в детстве. Рассказывают, что в трехлетнем возрасте он удивил окружающих, поправив расчеты своего отца с каменщиками. Однажды в школе (Гауссу в то время было 10 лет) учитель предложил классу сложить все числа от 1 до 100. Пока он диктовал задание, у Гаусса уже был готов ответ, на его грифельной доске было написано: 101 • 50 = 5050. 389. Попробуйте догадаться, как Карл Гаусс складывал числа от 1 до 100. 390. Из проволоки длиной 15 м делают обручи длиной 2 м. На сколько обручей хватит проволоки? Можно ли изготовить 4 обруча? 8 обручей? 391. Вычислите, выбирая удобный порядок выполнения действий: а) 937 - (137 + 793); г) (747 + 896) - 236; 392. На одной грядке посадили 30 кустов клубники, а на другой k кустов. Погибло 6 кустов. Сколько кустов клубники осталось на грядках? Составьте выражение для решения задачи и найдите его значение при k - 26; 35. 393. Найдите значение выражения, предварительно упростив его: а) (Ь + 179) - 89 при b = 56; 75; 394. Найдите значение выражения: 1) 34 • 27 + 1638 : 39; 3) (321 - 267) • (361 - 215) : 219; 395. Решите уравнение: а) 395 + х = 864; в) 300 - у = 206; д) 166 = m- 34; 396. Решите уравнение и выполните проверку: а) (х - 87) - 27 = 36; б) 87 - (41 + у) = 22. 397. Решите с помощью уравнения задачу: а) Продолжительность дня с 7 октября до 19 ноября уменьшилась на 3 ч и стала равной 8 ч. Какой была продолжительность дня 7 октября? На второй остановке вошли 10 человек, а на третьей — вышли 12 человек, после чего в автобусе осталось 17 человек. Сколько человек вошли в автобус на первой остановке? 398. Мотоциклист едет из города в село, расстояние до которого 120 км. Сколько километров ему осталось проехать, если он уже проехал а км? 399. Купили дюжину (дюжина — 12) бутылок фруктовой воды, а в обмен сдали 8 пустых бутылок. Сколько денег доплатили? Узнайте, сколько стоит бутылка фруктовой воды и сколько пустая бутылка, и решите задачу. 400. Имелось 65 л фруктового сока. Из них 20 л дали детям во время завтрака, а остальной сок разлили в трехлитровые банки. Сколько банок для этого потребовалось? 401. Запишите все трехзначные числа, которые можно записать только с помощью цифр 5, 3 и 0. 402. Масса 11 ящиков яблок 4 ц 62 кг, а масса 18 ящиков груш 6 ц 12 кг. На сколько килограммов масса одного ящика яблок больше масры одного ящика груш? 403. Найдите значение выражения: а) (37 296 : 37 - 17 780 : 35) : 250; В наше время почты все народы пользуются счетом десятками, сотнями, тысячами, то есть десятичной системой счисления. В ней, как вы уже знаете, значение цифры зависит от места (позиции), которое она занимает в записи числа. Поэтому такую систему счисления называют позиционной. Раньше некоторые народы применяли другие системы счета. В теплых странах Африки и Америки, где люди ходили босыми, для счета применялись не только пальцы рук, но и пальцы ног. Получался счет двадцатками. А пять тысяч лет назад в некоторых странах Востока пользовались шестидесятеричной системой счисления, то есть системой счисления с основанием Эта система была первой позиционной системой. На рисунке показано, как в этой системе выглядела запись некоторых чисел.
Использование числа 10 как основания системы счисления связано с тем, что у людей на руках 10 пальцев, которые удобнее всего было использовать при счете. Но основание системы счисления, конечно, может быть любым числом. Например, современные ЭВМ (электронные вычислительные машины) считают в двоичной системе (основание 2), так как при этом используются только два состояния: «есть сигнал» и «нет сигнала».
Видео по математике скачать, домашнее задание, учителям и школьникам на помощь онлайн Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: