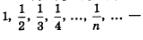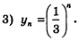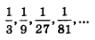|
Гипермаркет знаний>>Математика>>Математика 10 класс>> Числовые последовательности
§ 29. Числовые последовательности
Что такое числовая последовательность и как она задается, вам известно из курса алгебры 9-го класса. Напомним соответствующее определение. Определение 1. Функцию вида Иногда для обозначения последовательности используется запись (уn). Последовательности можно задавать различными способами, например словесно, когда правило задания последовательности описано словами, без указания каких-то формул. Так, словесно задается последовательность простых чисел:
Говорят, что последовательность задана аналитически, если указана формула ее п-го члена. Приведем три примера. 1) уп =п2. Это — аналитическое задание последовательности Указав конкретное значение п, нетрудно найти член последовательности с соответствующим номером. Если, например, п =9, 2) уп =С. Здесь речь идет о последовательности Такую последовательность называют постоянной (или стационарной). 3) уп =2n. Это — аналитическое задание последовательности Рекуррентный способ задания последовательности состоит в том, что указывают правило, позволяющее вычислить п-й член последовательности, если известны ее предыдущие члены. Например, арифметическая прогрессия — это числовая последовательность (а„), заданная рекуррентно соотношениями: Геометрическая прогрессия — это числовая последовательность , заданная рекуррентно соотношениями:
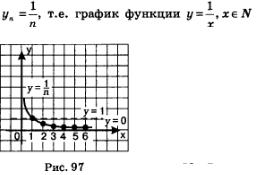
2. Свойства числовых последовательностей Числовая последовательность — частный случай числовой функции, а потому некоторые свойства функций (ограниченность, монотонность) рассматривают и для последовательностей. Определение 2. Последовательность (у„) называют ограниченной сверху, если все ее члены не больше некоторого числа. Иными словами, последовательность (у„) ограничена сверху, если существует числом такое, что для любого л выполняется неравенство уn<М. Число М называют верхней границей последовательности. Например, последовательность -1, -4, -9, -16, ...,-п2, ... ограничена сверху. В качестве верхней границы можно взятьчисло -1 или любое число, которое больше, чем -1, например 0. Определение 3. Последовательность (у„) называют ограниченной снизу, если все ее члены не меньше некоторого числа. Иными словами, последовательность (уn) ограничена снизу, если существует число т такое, что для любого л выполняется неравенство у„>M. Число m называют нижней границей последовательности. Например, последовательность 1, 4, 9, 16, ..., п2, ... ограничена снизу. В качестве нижней границы можно взять число 1 или любое число меньше 1. Если последовательность ограничена и сверху, и снизу, то ее называют ограниченной. Например, Если построить график последовательности
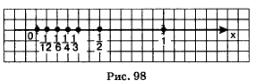
Особенно наглядным становится свойство ограниченности последовательности, если члены последовательности отметить точками на числовой прямой. Ограниченность последовательности означает, что все члены последовательности (точнее, соответствующие им точки прямой) принадлежат некоторому отрезку. Так, изобразив члены последовательности точками на числовой прямой, замечаем, что все они принадлежат отрезку [0, 1] (рис. 98).
Определение 5. Последовательность (у„) называют убывающей, если каждый ее член меньше предыдущего:
А.Г. Мордкович Алгебра 10 класс
Содержание урока
Если у вас есть исправления или предложения к данному уроку, напишите нам. Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум. |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: