|
Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Биссектриса угла. Полные уроки
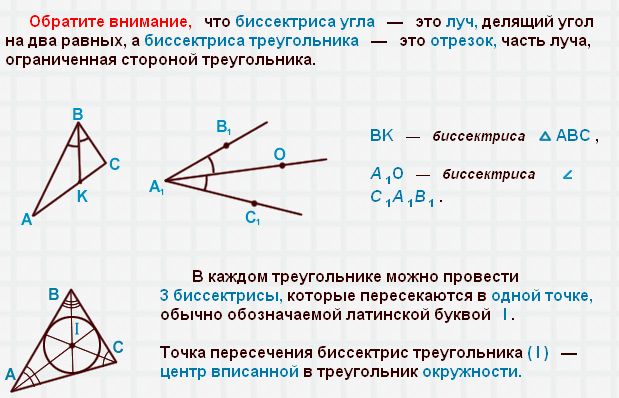
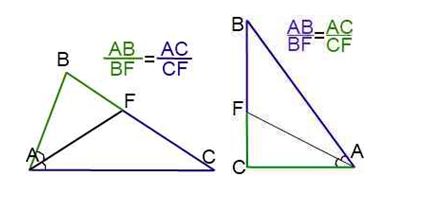
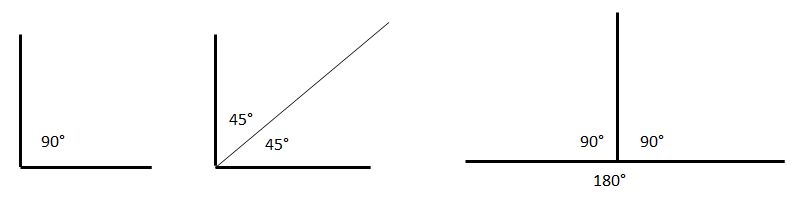
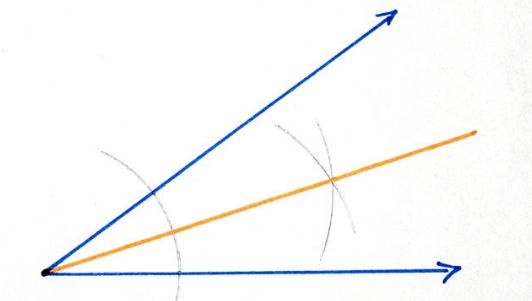
Тема урокаБиссектриса угла Цели урока• Пополнить знания школьников о биссектрисе угла и ее свойствах; Задачи урока• Расширить знания учеников о биссектрисе угла; План урока1. Раскрытие главной темы урока о биссектрисе угла; Биссектриса углаСегодняшний урок мы с вами посвятим теме биссектрисы. Давайте вспомним определения биссектрисы. Биссектрисой является геометрическое место точек, равноудаленное от сторон угла. Если говорить проще, то биссектриса – это линия, разделяющая угол пополам. Биссектрисой угла - луч, выходящий из вершины угла и делящий его на два других равных угла. Слово «биссектриса» в переводе с французского языка обозначает, как надвое рассекающая или равноделящая угол пополам. Биссектриса треугольникаКроме биссектрисы угла еще бывает биссектриса треугольника, ведь треугольник содержит целых три угла, соответственно каждый треугольник может иметь три разных биссектрисы. Что же такое биссектриса треугольника? Биссектриса треугольника является отрезком биссектрисы угла, соединяющим в треугольнике его вершину с точкой на противоположной стороне. Биссектриса треугольник обладает определенными уникальными свойствами. Так, например, она разделяет противоположную сторону на отрезки, которые являют пропорциональными другим двум сторонам. Что касается прямоугольного треугольника, то его биссектрисы именно острых углов, когда пересекаются, образуют угол именно в 45 градусов. К тому же, не стоит забывать и такое свойство биссектрис треугольника, как то, что пересекаются они строго в центре вписанного в треугольник круга. Ну а самое интересное то, что для равнобедренного треугольника линия, которая проведена к основанию, будет и биссектрисой, и медианой, и высотой. Соответственно и обратное правило, что если медиана, высота и биссектриса, которое проведены из одной вершины треугольника, совпадают, то перед нами равнобедренный треугольник. А какие вы можете вспомнить свойства прямоугольного и равнобедренного треугольника? Построение биссектрисыБиссектрису угла строится с помощью транспортира, при использовнии его градусной меры. Чтобы приступить к построению биссектрисы, мы берем и делим градусную меру пополам и, отложив на одной стороне вершины градусную меру половинного угла, и тогда вторая половина становится биссектрисой заданного угла. Берем заданный угол, который имеет градусную меру в девяносто градусов, и с помощью биссектрисы получаем два построенных угла по 45 градусов. Развернутый угол при помощи биссектрисы разделяет угол на 2 прямых угла. Тупой же угол при построении биссектрисы разделяет его на 2 острых угла. Из определения биссектрисы нам известно, что она является лучом, разделяющим угол пополам. Чтобы построить биссектрису, значит, нужно угол разделить пополам. Алгоритм построения биссектрисы угла1. Вначале чертим окружность с центром в вершине угла таким образом, чтобы она пересекала его стороны. 2. Далее делаем замеры циркулем расстояния между точками, где пересекается сторона угла с окружностью. 3. Чертим 2 окружности радиусом так, чтобы они имели точку пересечения внутри этого угла. 4. Теперь проводим из вершины угла луч таким методом, чтобы он проходил через точку пересечения этих окружностей. Этот луч и является биссектрисой данного угла. А теперь давайте попробуем доказать, что полученный луч является биссектрисой этого угла. Возьмем на примере двух треугольников, у которых одна сторона общая, то есть отрезок от вершины до точки пересечения окружностей, которую мы получили в 3п. 2-я пара соответствующих сторон – это полученные в 1п., отрезки, которые идут от вершины угла до точек пересечения окружности с его сторонами. Третья пара соответствующих сторон - это соответственно отрезки, полученные в 1п. от точек пересечения окружности, до точки пересечения окружностей, но полученных в 3п. Следовательно, 2 пары данных отрезков равны, поскольку являются радиусами одной или двух окружностей, но с одинаковым радиусом. Отсюда следует, что по всем трем сторонам треугольники равны. Известно, что когда треугольники равны, то равны и их углы. Поэтому при вершине два новых угла и данных угла по условию задачи равны, следовательно, что построенный луч будет биссектрисой.
Занимательная информация о биссектрисеЗнали ли вы, что существует такая наука, которая называется мнемоника, что в переводе с греческого языка обозначает искусство запоминания. И чтобы лучше запомнить определение биссектрисы существует такое мнемоническое правило, по которому биссектриса – это крыса, которая бегает по углам и делит угол пополам. Известно ли вам, что еще Архимед использовал теорему о биссектрисе. Он ее применял для деления основания на части, которые пропорциональны боковым сторонам с целью определения длины полу сторон двенадцати угольника, 24-угольника и т. д. Легенда о биссектрисе углаСказка о двух Углах и Биссектрисе, или Образование Смежного угла. Однажды два угла повстречались на одной площади. Старшему углу было около 130 градусов, а младшему всего пятьдесят. Так как это сказка, то заменим годы на градусы. Вот они встретились и начали спорить, кто из них лучше и важнее. Старший считал, что приоритет на его стороне, так как он старше, мудрее и больше на своем веку повидал за свои 130°. Младший наоборот твердил, что он моложе, потому сильнее и выносливее. И чтобы спор не длился вечность, они приняли решение провести турнир. Об этих состязаниях узнала Биссектриса и решила победить своих врагов одновременно и возглавить Геометрию. И вот настало долгожданное время турнира, на котором было 2 Угла. В момент полного разгара сражений появилась Биссектриса и решила принять участие. Но тут в бой с Биссектрисой вступил вначале старший Угол, затем подтянулся и младший, и победа все равно оказалась на стороне Биссектрисы. Биссектриса была счастлива, представляя себя в роли правительницы. Но старший Угол с младшим сдаваться не собирались и решили проучить заносчивую злодейку. Биссектриса, радуясь и торжествуя победу, даже не обратила внимание, что вместо 2-х ее противников возник Смежный угол, который в один момент победил Биссектрису. С того момента Биссектрисе пришлось служить королю, а два Угла стали одним целым со Смежным Углом и яро защищают Геометрию от всяких врагов. Предмети > Математика > Математика 7 класс |
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний - Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов -
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других "взрослых" тем.
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: