Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Геометрические фигуры. Полные уроки

Параллельные прямые.

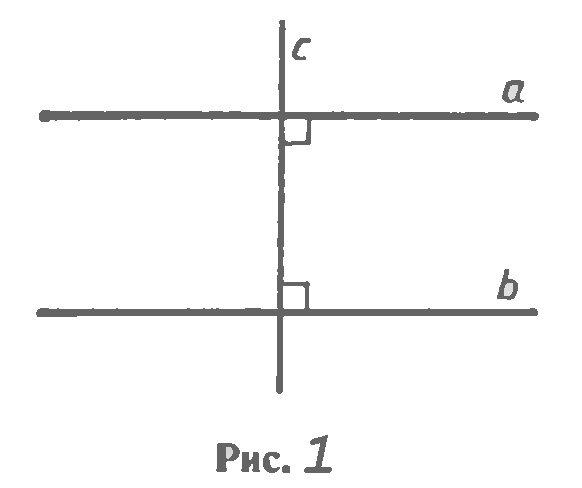
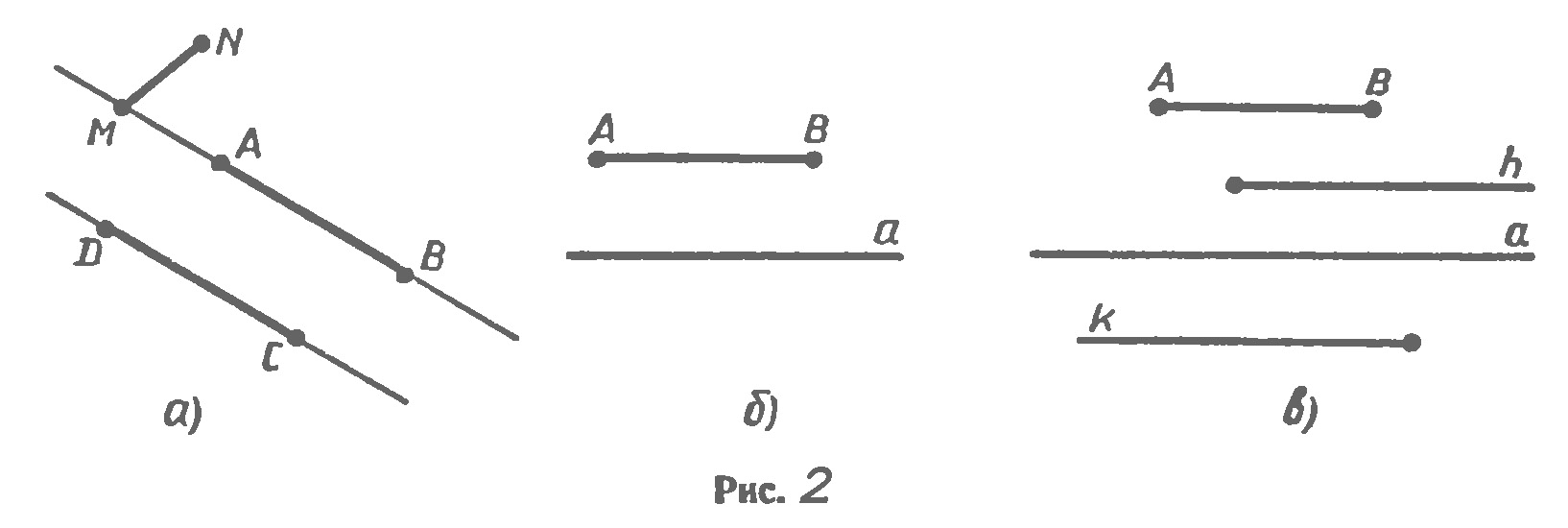
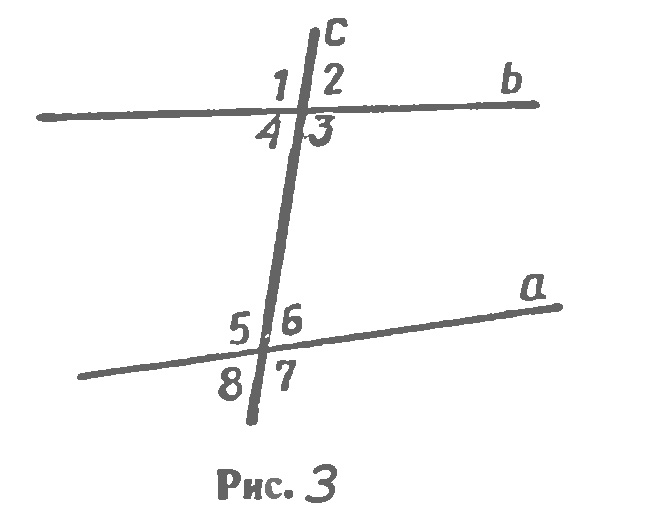
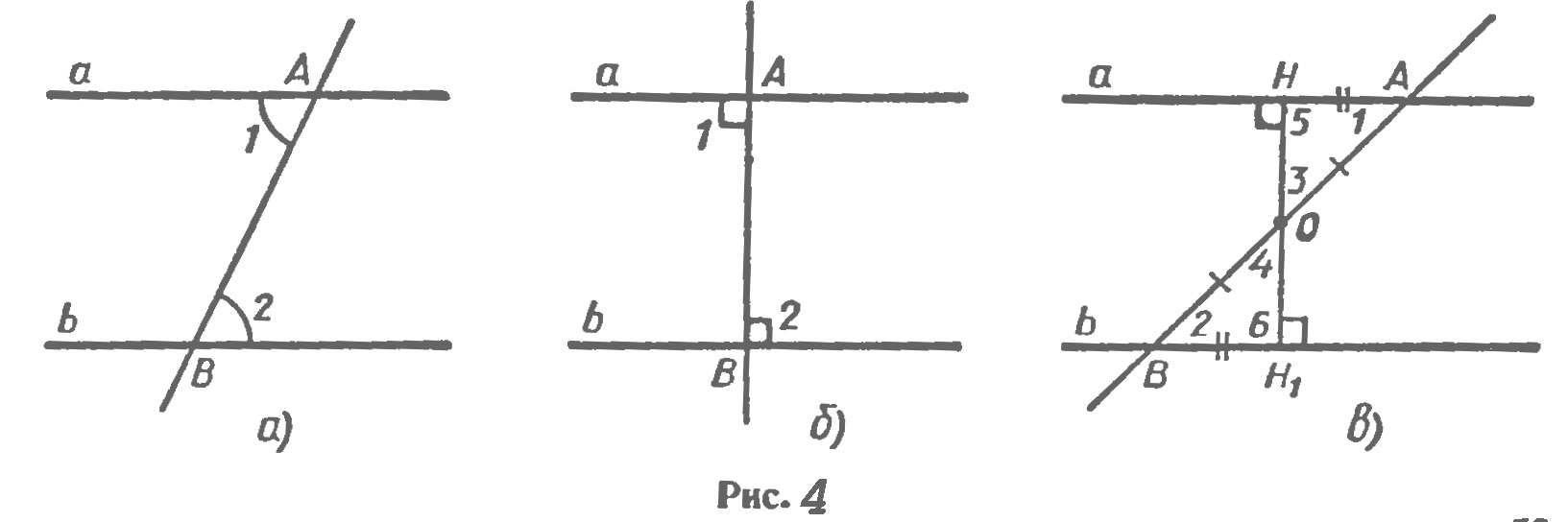
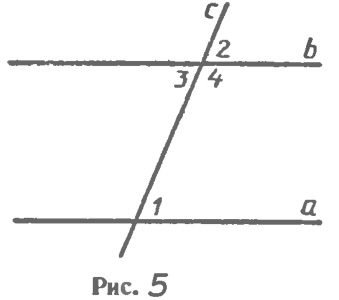
Определение. Две прямые на плоскости называются параллельными, если они не пересекаются.

Параллельность прямых а и b обозначают так: а||b. На рисунке 1 изображены прямые a и b, перпендикулярные к прямой с. Такие прямые а и b не пересекаются, т. е. они параллельны.

Наряду с параллельными прямыми часто рассматривают параллельные отрезки. Два отрезка называются параллельными, если они лежат на параллельных прямых. На рисунке (рис. 2,а) отрез­ки АВ и СD параллельны (АВ||СО) а отрезки МN и СD не параллельны. Аналогично определяется параллельность отрезка и прямой (рис. 2,б), луча и прямой, отрезка и луча, двух лучей(рис. 2,в).

Признаки параллельности двух прямых.

Прямая с называется секущей ми отношению к прямым а и b, если она пересекает их в двух точках (рис. 3). При пересечении прямых а и b секущей с образуется восемь углов, которые на рисунке 3 обозначены цифрами. Некоторые пары этих углов имеют специальные названия:

накрест лежащие углы: 3 и 5, 4 и 6;

односторонние углы: 4 и 5, 3 и 6; соответственные углы: 1 и 5, 4 и 8, 2 и 6, 3 и 7.

Рассмотрим три признака параллельности двух прямых, связанные с этими парами углов.

Теорема. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых а и b секущей АВ накрест лежащие углы равны: ∠1=∠2 (рис. 4, а).

окажем, что а||b. Если углы 1 и 2 прямые (рис. 4, б), то прямые а и b перпендикулярны к прямой АВ и, следовательно, параллельны. Рассмотрим случай, когда углы 1 и 2 не прямые. Из середины О отрезка АВ проведем перпендикуляр ОН к прямой а (рис. 4, в). На прямой b от точки В отложим отрезок ВН1 равный отрезку AH, как показано на рисунке 4, в, и проведем отрезок ОН1. Треугольники ОНА и ОН1В равны по двум сторонам и углу между ними (АО=ВО. АН=ВН1 ∠1=∠2), поэтому ∠3=∠4 и ∠15=∠16. Из равенства ∠3=∠4 следует, что точка Н1 лежит на продолжении луча ОН, т. е. точки Н, О и Н1 лежат на одной прямой, а из равенства ∠5=∠6 следует, что угол 6 — прямой (так как угол 5 — прямой). Значит, прямые а и b перпендикулярны к прямой НН1 поэтому они параллельны. Теорема доказана.

Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.

Доказательство. Пусть при пересечении прямых а и b секущей с соответственные углы равны, например ∠1=∠2 (рис. 5). Так как углы 2 и 3 - вертикальные, то ∠2=∠3. Из этих двух равенств следует, что ∠ 1=∠3. Но углы 1 и 3 — накрест лежащие, поэтому прямые а и b параллельны. Теорема доказана.

Теорема. Если при пересечении двух прямых секущей сумма односторонних углов равна 180°, то прямые параллельны.

Доказательство. Пусть при пересечении прямых а и b секущей с сумма односторонних углов равна 180°, например ∠1+∠4=180° (см. рис. 5). Так как углы 3 и 4 — смежные, то ∠3+∠4=180°. Из этих двух равенств следует, что накрест лежащие углы 1 и 3 равны, поэтому прямые а и b параллельны. Теорема доказана.

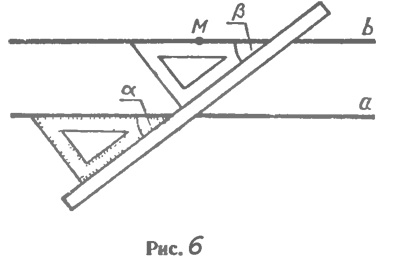
Практические способы построения параллельных прямых.

Признаки параллельности прямых лежат в основе способов построения параллельных прямых с помощью различных инструментов, используемых на практике. Рассмотрим, например, способ построения параллельных прямых с помощью чертежного угольника и линейки. Чтобы построить прямую, проходящую через точку М и параллельную данной прямой а, приложим чертежный угольник к прямой а, а к нему линейку так, как показано на рисунке 103. Затем, передвигая угольник вдоль линейки, добьемся того, чтобы точ ка М оказалась на стороне угольника, и проведем прямую b. Прямые а и b параллельны, так как соответственные углы, обозначенные на рисунке 103 буквами альфа

и бета, равны.

Еще есть способ построения параллельных прямых при помощи рейсшины. Этим способом пользуются в чертежной практике.

Аналогичный способ применяется при выполнении столярных работ, где для разметки параллельных прямых используется малка (две деревянные планки, скрепленные шарниром).

Интересный факт:

Особое место в истории математики занимает пятый постулат Евклида (аксиома о параллельных прямых). Долгое время математики безуспешно пытались вывести пятый постулат из остальных постулатов Евклида и лишь в середине XIX века благодаря исследованиям Н. И. Лобачевского, Б. Римана и Я. Бойяи стало ясно, что пятый постулат не может быть выведен из остальных, а система аксиом, предложенная Евклидом, не единственно возможная.

Аксиома параллельных прямых

Еще древние греки придумали простой способ: как провести циркулем и линейкой через точку А, лежащую вне данной прямой l, другую прямую m, не пересекающую прямую l. Но единственно ли решение этой задачи? Или через точку А можно провести несколько разных прямых, не пересекающих исходную прямую m?

Евклид, видимо, первый среди эллинов понял, что ответ на этот вопрос нельзя получить, исходя из прочих свойств прямых и точек – тех, которые он сформулировал в виде аксиом и постулатов. Нужно ввести дополнительный постулат о единственности искомой прямой m – и назвать эту прямую параллельной!

А возможны ли иные формулировки постулата о параллельных прямых – не совместимые с постулатом Евклида? Например, можно предположить существование нескольких разных прямых, не пересекающих данную прямую l и проходящих через общую точку А. Приведет ли такое предположение к логическому противоречию или нет? Если нет, то возможны иные геометрии, кроме евклидовой!

Первую неевклидову геометрию изобрели в 1820-е годы сразу три талантливых математика: немец Карл Гаусс, русский Николай Лобачевский и венгр Янош Бойяи. Русский математик оказался самым смелым и упорным из троих открывателей. Он первый опубликовал свою книгу с предсказанием замечательных свойств неевклидовых фигур. Например, на плоскости Лобачевского сумма внутренних углов треугольника всегда меньше 180 градусов. Она принимает разные значения для разных треугольников; при этом два подобных треугольника обязательно равны!

В конце 19 века геометры Клейн и Пуанкаре изобрели довольно простые модели поверхностей, на которых воплощается геометрия Лобачевского. Еще раньше Риман заметил, что на обычной сфере воплощена третья возможная геометрия (проективная): в ней «параллельных» прямых вовсе нет, а сумма внутренних углов треугольника всегда больше, чем 180 градусов.

До начала 20 века считалось, что неевклидовы геометрии могут быть полезны только внутри математической науки. Но в 1910-е годы Эйнштейн создал Общую Теорию Относительности: она оказалась четырехмерным воплощением неевклидовой геометрии Лобачевского. С тех пор физики верят, что каждая непротиворечивая математическая конструкция воплощена где-нибудь в Природе. Возможно, что так оно и есть.

Вопросы:

1. Какие прямые называются параллельными?
2. Какие практические способы построения параллельных прямых существуют.?
   

Список использованных источников:<span lang="RU" />

1. <span lang="RU" />Федеральный общеобразовательный стандарт. Вестник образования. №12,2004.
2. Атанасян, Геометрия 7-9 класс.
3. П.И. Алтынов. Математика. 2600 тестов и проверочных заданий для школьников и поступающих в вузы.
   Издательский дом «Дрофа», 1999.
   
4. Газета «Математика» № 27, 2000 год.
   

Отредактировано и выслано Потурнаком С .А.

Если у вас есть исправления или предложения к данному уроку, напишите нам.

Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.