|
Гипермаркет знаний>>Математика>>Математика 9 класс>>Математика: Функции y = xn(n є N), их свойства и графики
Функции y = xn(n є N), их свойства и графики
Функцию вида у = хn, где n = 1, 2, 3, 4, 5, ..., называют степенной функцией с натуральным показателем.
Две степенные функции мы с вами уже изучили: у = х (т.е. у — х1) и у = х2. Этим перечень наших достижений исчерпывается, ибо, начиная с n = 3, мы о функции у = хn пока ничего не знаем. Как выглядят графики функций у = х3,у = х4,у = х5,у = х6 и т.д.? Каковы свойства этих функций? Об этом и степенная пойдет речь в настоящем параграфе. Правда, в § 10 функция одно свойство мы с вами предусмотрительно обсудили: доказали, что у = х4 — четная функция, а у = х3 — нечетная функция. И это, кстати, нам сейчас очень пригодится. Мы ведь знаем, что график четной функции симметричен относительно оси ординат, а график нечетной функции симметричен относительно начала координат. Значит, мы можем и для функции у = х4, и для функции у — х3 поступить так: рассмотреть эти функции на луче, построить их графики (на указанном луче). Затем, используя симметрию, построить график функции на всей числовой прямой и с помощью графика перечислить свойства функции по той схеме, которую мы выработали в предыдущих параграфах (добавив свойство четности).
1. Функция 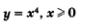
Составим таблицу значений для этой функции:
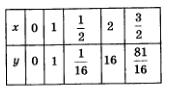
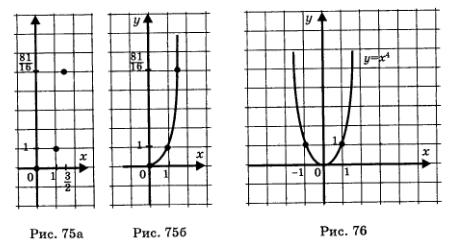
Построим точки 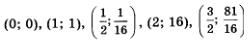 на координатной плоскости (рис. 75а); они намечают некоторую линию, проведем ее (рис. 756). на координатной плоскости (рис. 75а); они намечают некоторую линию, проведем ее (рис. 756).
2. Функция у = х4
Рассмотрим график, изображенный на рис. 75б. Добавив к нему линию, симметричную построенной относительно оси ординат, получим график функции у = x4 (рис. 76). Он похож на параболу (но параболой его не называют).
Прежде чем перечислить свойства функции, заметим, что мы будем придерживаться того же порядка ходов, который использовали в § 9, с одной поправкой: свойству четности функции отведем вторую позицию.
Свойства функции у = х4:

Эти свойства мы прочитали по графику, что, в общем-то, как мы уже подчеркивали выше, в математике не принято. Обычно поступают наоборот: исследуют свойства функции, а потом, опираясь на результаты проведенного исследования, строят ее график. В состоянии ли мы с вами уже теперь действовать так, как принято в математике? Пока еще не совсем. Из перечисленных выше восьми свойств очевидно первое (поскольку любое число х можно возвести в четвертую степень). В предыдущем параграфе доказано второе свойство. Можно доказать и третье: в самом деле, если 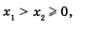 то, по свойству числовых неравенств, то, по свойству числовых неравенств,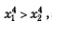 а это и означает возрастание функции на луче [0, +оо) (см. определение 1 из § 9). Можно доказать четвертое свойство: для любого значения х справедливо неравенство х4 > 0, а это и означает ограниченность функции снизу (см. определение 3 из § 9). Очевидно пятое свойство. Что же не доказано, где мы вынуждены пока опираться на геометрическую интуицию? Не доказаны свойства 6, 7 и 8. а это и означает возрастание функции на луче [0, +оо) (см. определение 1 из § 9). Можно доказать четвертое свойство: для любого значения х справедливо неравенство х4 > 0, а это и означает ограниченность функции снизу (см. определение 3 из § 9). Очевидно пятое свойство. Что же не доказано, где мы вынуждены пока опираться на геометрическую интуицию? Не доказаны свойства 6, 7 и 8.
Впрочем, при желании можно дать некоторое пояснение (не доказательство) и свойству выпуклости функции вниз. Покажем, например, что на отрезке [0, +оо), где а > 0, график функции у = х4 расположен ниже отрезка ОА (рис. 77).
На интервале (0, а) возьмем произвольную точку хг и восставим из этой точки перпендикуляр к оси х до пересечения с графиком функции у = х4 (в точке Р) и с прямой ОА (в точке М) (рис. 77). Ордината точки Р равна х4, а чему равна ордината точки М? Давайте подсчитаем.
Прямая ОА проходит через начало координат, значит, ее уравнение имеет вид у — kх. Эта прямая проходит через точку А(а; а4). Подставив координаты точки А в уравнение у = kх, получим равенство а4 = ка. Значит, к = а3, т.е. уравнение прямой ОА таково: у = а3х.
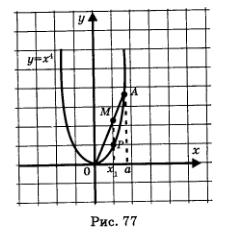
Теперь ясно, что ордината точки М равна а3х2.
Итак, ордината точки Р равна 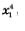 , а ордината точки М равна а3хг Какое из этих чисел больше? Имеем 0 < х1 < а, значит, по свойствам числовых неравенств, х3 < а3 и далее , а ордината точки М равна а3хг Какое из этих чисел больше? Имеем 0 < х1 < а, значит, по свойствам числовых неравенств, х3 < а3 и далее 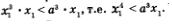 Что означает последнее неравенство? То, что точка Р располагается ниже точки М. А отсюда можно сделать вывод: если провести произвольную прямую ОА, то окажется, что график функции у = х4 на отрезке [0, а] лежит ниже соответствующего участка прямой ОА. Что означает последнее неравенство? То, что точка Р располагается ниже точки М. А отсюда можно сделать вывод: если провести произвольную прямую ОА, то окажется, что график функции у = х4 на отрезке [0, а] лежит ниже соответствующего участка прямой ОА.
3. Функция у — х2n
Речь идет о функциях у = х6, у = х8 и вообще о степенной функции счетным показателем степени. График любой такой функции похож на график функции у = х4 (рис. 76), только его ветви более круто направлены вверх.
Отметим еще, что кривая у = х2n касается оси х в точке (0; 0), т.е. одна ветвь кривой плавно переходит в другую, как бы прижимаясь к оси х.
4. Функция у - х3
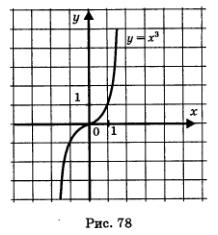
Заметим прежде всего, что у = х3 — нечетная функция, следовательно, ее график симметричен относительно начала координат. График функции 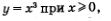 в принципе выглядит так же, как график функции в принципе выглядит так же, как график функции 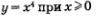 (рис. 756), нужно лишь учесть, что новая кривая чуть менее круто идет вверх и чуть дальше отстоит от оси х около начала координат. Добавив линию, симметричную построенной относительно начала координат, получим график функции у = х3 (рис. 78). Эту кривую называют кубической параболой. (рис. 756), нужно лишь учесть, что новая кривая чуть менее круто идет вверх и чуть дальше отстоит от оси х около начала координат. Добавив линию, симметричную построенной относительно начала координат, получим график функции у = х3 (рис. 78). Эту кривую называют кубической параболой.
Замечание.
Между прочим, это один из редких случаев, когда математики используют не очень удачный термин. Парабола — геометрическая фигура с определенными свойствами. Линия, изображенная на рис. 78, этими свойствами не обладает, поэтому лучше было бы придумать ей другое название, без использования термина «парабола» («кубическая парабола» — это что-то вроде «квадратной окружности»). Но термин «кубическая парабола» прижился в математике, придется и нам его использовать.
Отметим некоторые геометрические особенности кубической параболы у = х3. У нее есть центр симметрии — точка (0; 0), которая отделяет друг от друга две симметричные части кривой; эти симметричные части называют ветвями кубической параболы. Обратите внимание: когда одна ветвь кубической параболы переходит через начало координат в другую ветвь, то это происходит плавно, без излома.
Свойства функции у = х3:
1)D(f) = (-00,+00);
2) нечетная функция;
3) возрастает;
4) не ограничена ни снизу, ни сверху;
5) нет ни наименьшего, ни наибольшего значений;
6) непрерывна;
7) Е(f) = (-оо, +00);
8) выпукла вверх при х < 0, выпукла вниз при х > 0.
5. Функция у = х2n+1
Речь идет о функциях у = х3, у — хb, у = х1 и вообще о степенной функции снечетным показателем степени (3, 5, 7, 9 и т.д.). График любой такой функции похож на график функции у — аx4 (рис. 78), только чем больше показатель, тем более круто направлены вверх (и соответственно вниз) ветви графика. Отметим еще, что кривая у = х2n+1 касается оси х в точке (0; 0).
Пример 1.
Решить уравнение х5 = 3 - 2х.
Решение.
1) Рассмотрим две функции: у — х5 и у= 3 - 2х.
2) Построим график функции у = хъ (рис. 79).
3) Построим график линейной функции у = 3 - 2х. Это — прямая линия, проходящая через точки (0; 3) и (1; 1) (рис. 79).
4) Построенные графики пересекаются в точке А(1; 1), причем простая проверка показывает, что координаты точки А(1; 1) удовлетворяют и уравнению у = х5, и уравнению у = 3 - 2х. Значит, уравнение имеет один корень: х = 1 — это абсцисса точки А.
О т в е т: 1.
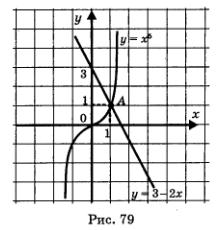
Между прочим, геометрическая модель, представленная на рис. 79, наглядно иллюстрирует следующее утверждение, которое иногда позволяет изящно решить уравнение:
Если функция у = f(х) возрастает, а функция y = g(х) убывает и если уравнение f(х) = g(х) имеет корень, то только один.
Вот как, опираясь на это утверждение, мы можем решить уравнение из примера 1 без чертежа:
1) заметим, что при х = 1 выполняется равенство 15 = 3 - 2 • 1, значит, х = 1 — корень уравнения (этот корень мы угадали);
2) функция у—3-2х убывает, а функция у — х5 возрастает, значит, корень у заданного уравнения только один и этим корнем является найденное выше значение х = 1.
Пример 2.
Построить график функции у = (х - I)6 - 2.
Решение.
1) Перейдем к вспомогательной системе координат с началом в точке (1; -2) (пунктирные прямые х = 1 и у = -2 на рис. 80а).
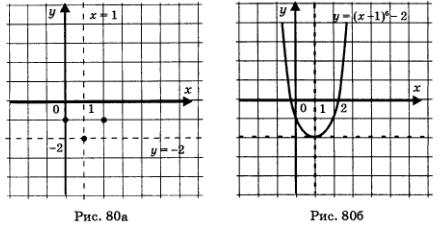
2) Привяжем функцию у = х6 к новой системе координат. Для этого выберем контрольные точки для функции у = х6: (0; 0), (1; 1), (-1; 1), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 80а). Затем через контрольные точки проведем линию, похожую на ту, которая изображена на рис. 76, — это и будет требуемый график (рис. 80b).
А.Г. Мордкович Алгебра 9 класс
Материалы по математике онлайн, задачи и ответы по классам, планы конспектов уроков по математике скачать
Содержание урока
 конспект урока конспект урока
 опорный каркас опорный каркас
 презентация урока презентация урока
 акселеративные методы акселеративные методы
 интерактивные технологии
Практика интерактивные технологии
Практика
 задачи и упражнения задачи и упражнения
 самопроверка самопроверка
 практикумы, тренинги, кейсы, квесты практикумы, тренинги, кейсы, квесты
 домашние задания домашние задания
 дискуссионные вопросы дискуссионные вопросы
 риторические вопросы от учеников
Иллюстрации риторические вопросы от учеников
Иллюстрации
 аудио-, видеоклипы и мультимедиа аудио-, видеоклипы и мультимедиа
 фотографии, картинки фотографии, картинки
 графики, таблицы, схемы графики, таблицы, схемы
 юмор, анекдоты, приколы, комиксы юмор, анекдоты, приколы, комиксы
 притчи, поговорки, кроссворды, цитаты
Дополнения притчи, поговорки, кроссворды, цитаты
Дополнения
 рефераты рефераты
 статьи статьи
 фишки для любознательных фишки для любознательных
 шпаргалки шпаргалки
 учебники основные и дополнительные учебники основные и дополнительные
 словарь терминов словарь терминов
 прочие
Совершенствование учебников и уроков прочие
Совершенствование учебников и уроков
 исправление ошибок в учебнике исправление ошибок в учебнике
 обновление фрагмента в учебнике обновление фрагмента в учебнике
 элементы новаторства на уроке элементы новаторства на уроке
 замена устаревших знаний новыми
Только для учителей замена устаревших знаний новыми
Только для учителей
 идеальные уроки идеальные уроки
 календарный план на год календарный план на год
 методические рекомендации методические рекомендации
 программы программы
 обсуждения
Интегрированные уроки обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь - Образовательный форум.
|


















