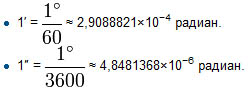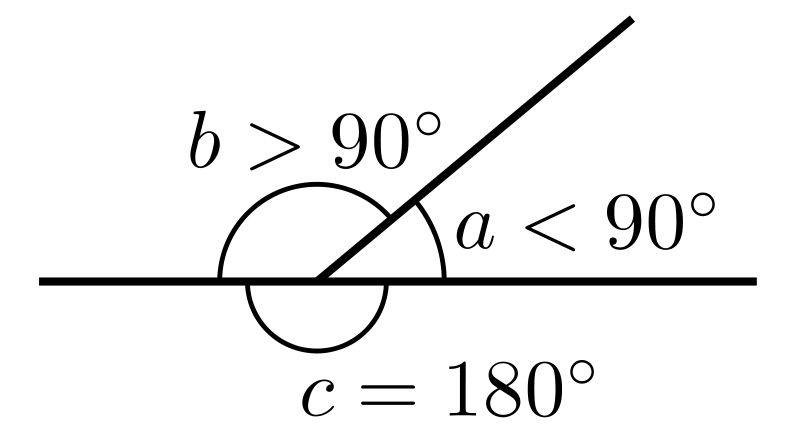Текущая версия на 14:07, 30 марта 2011

Гипермаркет знаний>>Математика>>Математика 7 класс. Полные уроки>>Геометрия: Вертикальные углы. Полные уроки

ТЕМА УРОКА: Вертикальные углы.

Цели урока:

• Образовательные – повторение, обобщение и проверка знаний по теме: “Вертикальные углы”; выработка основных навыков.
• Развивающие – развить внимание учащихся, усидчивость, настойчивость, логическое мышление, математическую речь.
• Воспитательные - посредством урока воспитывать внимательное отношение друг к другу, прививать умение слушать товарищей, взаимовыручке, самостоятельность.

Задачи урока:

• Формировать навыки в построении вертикальных углов с помощью линейки, транспортира и чертежного треугольника.
• Проверить умение учащихся решать задачи.

План урока:

1. Экскурс в историю геометрии, развитие геометрии.
   
2. Угол в геометрии, его величины.
   
3. Вертикальные углы.
   
4. Типы углов.

Историческая справка

Геометрия на Востоке

Первые шаги культуры всюду, где она возникала, в Китае, в Индии, в Ассирии, в Египте, были связаны с необ­ходимостью измерять расстояния и участки на земле, объемы и веса материалов, продуктов, товаров; первые значительные сооружения требовали нивелирования, выдержанной верти­кали, знакомства с планом и перспективой. Необходимость измерять промежутки времени требовала систематического наблюдения над движением светил, а следовательно, изме­рения углов. Всё это было неосуществимо без знакомства с элементами геометрии, и во всех названных странах основ­ные геометрические представления возникали частью неза­висимо друг от друга, частью — в порядке преемственной передачи. Однако точных сведений о познаниях египтян в области геометрии мы не имеем. Единственным первоисточником, дошедшим до нас, является папирус, написанный при фараоне Payee ученым писарем его Ахмесом (Ahmes) в период между 2000 и 1700 г. до нашей эры. Это — руководство, содержащее различного рода математические задачи и их решения; значительное большинство задач относится к ариф­метике, меньшая часть — к геометрии.

Из последних почти все связаны с измерением площадей прямолинейных фигур и круга, причем Ахмес принимает площадь равнобедренного треугольника  равной  произведению  основания  на   половину боковой  стороны,  а площадь  круга — равной  площади  ква­драта,  сторона  которого  меньше диаметра  на   1/3  его часть (это  дает  л=3,160...);   площадь  равнобочной   трапеции   он принимает равной произведению   полусуммы   параллельных сторон на боковую сторону. Как видно из нескольких других задач Ахмеса,  египтяне в эту пору знали, что углы прямо­угольного  треугольника   определяются   отношением   катетов. Как они пришли ко всем этим правилам, знали ли наиболее просвещенные   жрецы — хранители    египетской   науки, — что их данные являются лишь приближенными, об этом  мы не имеем  никаких сведений.  Столь же мало  знаем  мы о том, что прибавило к этим познаниям  египтян  следующее тыся­челетие; сколько-нибудь значительных успехов они во всяком случае не сделали. Трудно сказать вполне точно, что из этих сведений египтяне открыли сами и что они заимствовали от вавилонян и индусов. Несомненно лишь то, что геометриче­ские сведения  вавилонян  были  столь же  отрывочны и столь же  скудны.  Им  принадлежит деление окружности  на  360о; они имели сведения о параллельных линиях и точно воспро­изводили  прямые углы;   всё  это  было  им   необходимо   при астрономических  наблюдениях,  которые,  по-видимому,  глав­ным   образом   и   привели   к   их   геометрическим   знаниям. Вавилоняне  знали,  что  сторона  правильного   вписанного   в круг  шестиугольника   равна    радиусу. Характерным для этого первого, в известном смысле доисто­рического,   периода  геометрии  являются  две  стороны  дела: во-первых,   установление   наиболее  элементарного   геометри­ческого материала, прямо необходимого в практической ра­боте,   а  во-вторых,   заимствование этого   материала  из  при­роды   путем непосредственного   наблюдения   («чувственного восприятия»,   по   словам    Евдема    Родосского).    Наиболее характерное   выражение  этого   непосредственного   апеллиро­вания  к  интуиции  как  единственному   удостоверению   пра­вильности  высказанной  истины   мы   находим   у   индусского математика Ганеши.

Угол.

Угол – это геометрическая фигура  ( рис.1 ), образованная двумя лучами OA и OB ( стороны угла ), исходящими из одной точки O ( вершина угла ).

Файл:23102010 1.gif

Для обозначения угла имеется общепринятый символ: , предложенный в 1634 году французским математиком Пьером Эригоном.

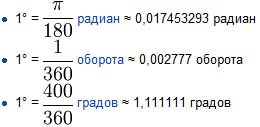
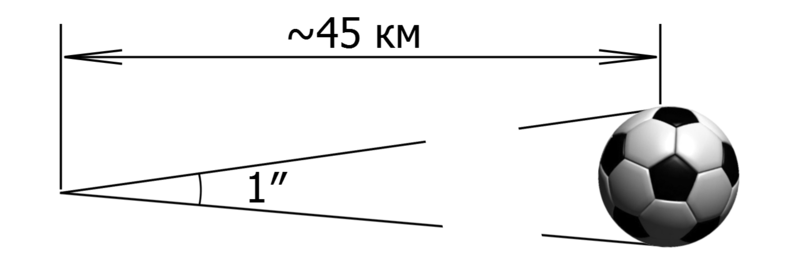
Градусная система измерения углов.

Здесь единицей измерения является градус ( его обозначение ° ) – это поворот луча на 1 / 360  полного оборота. Таким образом, полный оборот луча равен 360!. Один градус делится на  60 минут ( обозначение ‘ ); одна минута – соответственно на 60 секунд  ( обозначение “ ). Угол в 90° ( рис.2 ) называется прямым; угол, меньший, чем  90° ( рис.3 ), называется острым; угол, больший, чем 90° ( рис.4 ), называется тупым.

Файл:23102010 2.gif

Градус, минута, секунда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки Земной поверхности.

Градус (от лат. gradus — деление шкалы, шаг, ступень). Один оборот равен 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.

Деление окружности на 360° придумали аккадцы (вавилоняне) — соответственно делению года в вавилонском календаре на 360 дней.

По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается знаком ′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается знаком ″). Корни такого деления лежат также в Древнем Вавилоне, где использовалась шестидесятеричная система счисления.

Угловая секунда

Угловая секунда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла.

Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с). Соотношение между этими величинами определяется формулой 1c = 15″

Вертикальные углы.

Вертикальные углы пары углов с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

Вертикальные углы — два угла, которые образуются при пересечении двух прямых, эти углы не имеют общих сторон. Другими словами — два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Два вертикальных угла равны.

На рис. — две пары.

Файл:13012011 8.gif

∠2=∠1; ∠3=∠4;

Типы углов
Смежные углы — острый (a) и тупой (b). Развёрнутый угол (c)

Смежные углы — два угла с общей вершиной, одна из сторон которых — общая, а оставшиеся стороны лежат на одной прямой (не совпадая). Сумма смежных углов равна 180°. Вертикальные углы — два угла, которые образуются при пересечении двух прямых, эти углы не имеют общих сторон. Другими словами — два угла называют вертикальными, если стороны одного угла являются продолжениями сторон другого. Два вертикальных угла равны.

Интересный факт:

Геометрия Вселенной.

Чем дальше объект, тем в более раннюю эпоху мы его видим. Дальше всех находятся квазары, и мы видим их такими, какими они были миллиарды лет назад. Наблюдая распределение и движение галактик, скоплений, сверхскоплений, мы узнаем эти их свойства такими, какими они были в очень отдаленном, по нашим обычным понятиям, прошлом. Но по масштабам Вселенной разница в сотни миллионов лет не очень велика: ее расширение происходит в таком темпе, что плотность вещества Вселенной на современной стадии ее расширения заметно меняется лишь за миллиарды лет. Потому-то плотность в близкой к нам области Вселенной, где видны галактики, и представляется нам одинаковой, однородной. Если бы, однако, можно было заглянуть на более далекие расстояния, т. е. в более далекое прошлое, то мы, очевидно, обнаружили бы, что там (т. е. тогда) плотность больше, чем вблизи (т. е. сейчас). Снимок, сделанный в реальных лучах, показал бы, таким образом, Вселенную неоднородной по плотности: чем дальше от нас, тем плотнее. На таком снимке и само пространство, в соответствии с общими принципами эйнштейновской теории, должно быть неоднородным по своим геометрическим свойствам. Более того, на снимке в реальных лучах пространство всегда конечно по объему, независимо от того, какова судьба космологического расширения. Дело в том, что свет, приходящий к нам от далеких источников, испытывает за время своего распространения красное смещение: длины волн в электромагнитных колебаниях возрастают, а частоты убывают. Это, как мы говорили, следствие эффекта Доплера, обязанного космологическому расширению, относительному движению галактик. По закону Хаббла, чем дальше от нас источник, тем больше скорость его удаления от нас и, следовательно, больше красное смещение линий в его спектре. При этом существует такое большое, но вполне определенное, конечное расстояние, для которого длина волны приходящего света оказывается бесконечной, а частота принимаемого света обращается в нуль, и из-за этого источник становится для нас невидимым.

Квазары:

Вопросы:

1. Что такое угол?
2. Какие бывают типы углов?
3. Чему равно 2 в градусах?
4. Что такое вертикальный угол?
   

Список использованных источников:

1. Урок на тему "Углы" Автор: Марина Александровна, г. Киев
   
2. Урок на тему "Угол как геометрическая величина" Автор: Вилофич А. Н., г. Москва
3. Урок на тему  "Наглядная геометрия". 7-й класс. Автор: Самылина Марина Валентиновна, г. Киев
4. Павлов А. Н. Геометрия: Планиметрия в тезисах и решениях.
   
5. проект "Астрогалактика" 25 ноября 2006 
6. Гордин Р. К. Геометрия. Планиметрия. 7-9 классы.

Над уроком работали:

Марина Александровна

Потурнак С.А.

Вилофич А. Н.

Самылина М. В.

Поставить вопрос о современном образовании, выразить идею или решить назревшую проблему Вы можете на Образовательном форуме, где на международном уровне собирается образовательный совет свежей мысли и действия. Создав блог, Вы не только повысите свой статус, как компетентного преподавателя, а и сделаете весомый вклад в развитие школы будущего. Гильдия Лидеров Образования открывает двери для специалистов  высшего ранга и приглашает к сотрудничеству в направлении создания лучших в мире школ.